Лабораторная работа № 5 «Задачи на оптимальное распределение ресурсов»
Цель: на примере классических задач познакомиться с задачами на оптимальное распределение ресурсов и их практической реализацией в MS EXCEL с целью решения с помощью надстройки Поиск решения.
Программные средства: MS Excel, надстройка Solver (Поиск решения).
Распределение однородных ресурсов
Постановка задачи.
Найти оптимальное распределение 3-х машин по 4 работам, чтобы при условии исполнения заданных объемов общая стоимость всех произведенных работ была бы минимальной.
Начальные данные: матрица себестоимости работ; ресурсы машин (время); продуктивность машин; объем работ.
Экономико-математическая модель.
Найти такую матрицу распределения ресурсов, чтобы
Общие затраты=Матрица_себестоимости*Матрица_распределения → min
При ограничениях:
Сделано=Объем;
использованные ресурсы<=Ресурсы;
Матрица_распределения >=0.
Реализация в Excel.
Создаем таблицу с формулами, которые связывают план, ограничения и целевую функцию (Стоимость):
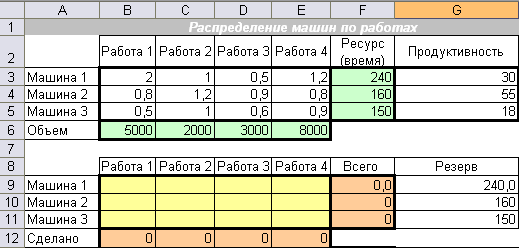
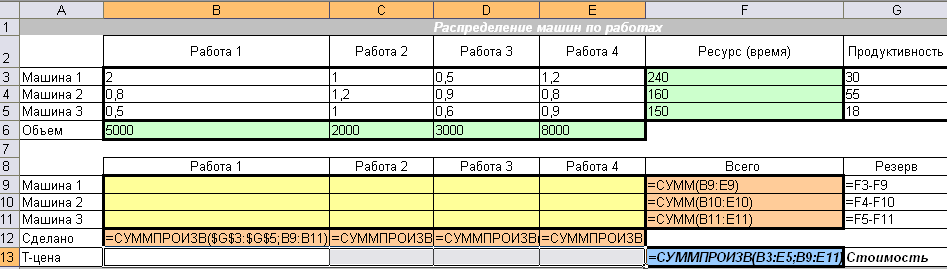
столбец «Всего» заполняем формулой суммы по строкам Матрицы_распределения;
столбец «Резерв» заполняем формулой: Ресурс-Всего;
строку «Сделано» заполняем формулой:
=СУММПРОИЗВ(Продуктивность; Работа_n);
в целевую ячейку вводим формулу:
=СУММПРОИЗВ(Матрица_себестоимости; Матрица_распределения).
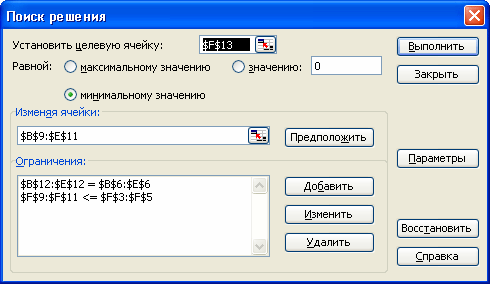
Запускаем программу Поиск решений командой Данные/Анализ/Поиск решения (В Excel 2007) Сервис/Поиск решения (В Excel 2003 и ниже). В полях Установить целевую ячейку, Изменяя ячейки, Ограничения вводим соответствующие адреса ячеек. Так как это линейная модель, то не забываем фиксировать в окне Параметры поиска решений переключатель на позицию Линейная модель и Неотрицательные значения. Нажимаем кнопку Выполнить и в появившемся окне Результаты поиска решения выводим отчет по устойчивости.
Анализ результатов.
При оптимальном плане (см. таблицу) общие затраты становятся 379,67 д. ед., при чем 1-я машина не загруженная полностью, её резерв становит 23,3.
Теневые цены полностью использованных ресурсов показывают, что с увеличением их ресурса общие затраты уменьшатся. Теневые цены объемов работ показывают, как будут увеличиваться общие затраты при увеличении объемов работ.
Нормированные стоимости указывают, на сколько увеличится общая стоимость работ, если мы принудительно поставим машину на «невыгодною работу».
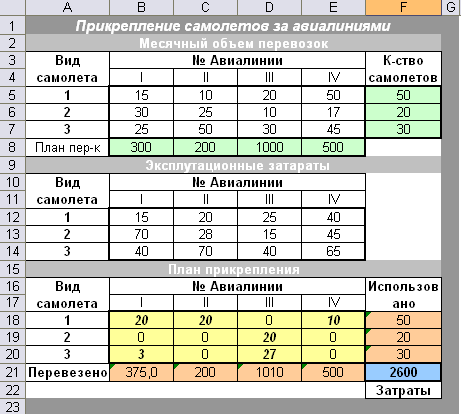
Прикрепление самолетов за авиалиниями
Постановка задачи.
А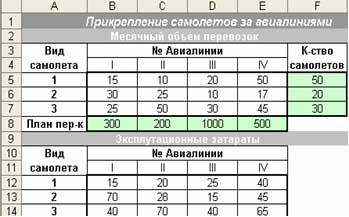
виакомпания
имеет 4 направления полетов (авиалиний)
для которых использует 3 вида самолетов,
которые имеются в ограниченных
количествах. Также есть таблица месячных
объемов перевозок определенного вида
самолета по соответствующей авиалинии
и таблица эксплуатационных затрат на
перевозку. Нужно найти оптимальное
прикрепление самолетов за авиалиниями,
чтобы затраты были минимальными, причем
объем перевозок должен быть не меньше
плана перевозок и все самолеты должны
быть задействованы.
Экономико-математическая модель.
Найти такое распределение самолетов по авиалиниям, чтобы:
Затраты = План_прикрепления*Эксплутационные_затраты → min.
При ограничениях:
Использовано(самолетов)=Количество(самолетов);
Перевезено>=План_перевозок;
все неизвестные больше нуля и целые числа.
Реализация в Excel.
Создаем таблицу с формулами, которые связывают план, ограничения и целевую функцию (Затраты):
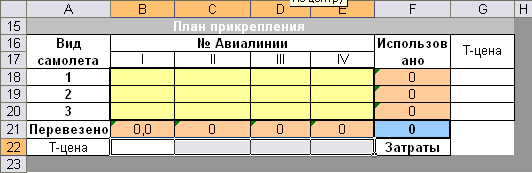
в столбец «Использовано» вводим формулы суммы по строкам матрицы прикрепления;
в строку «Перевезено» вводим формулы: =СУММПРОИЗВ(Объем_перевозок_авиалиния_n; План_авиалиния_n);
в целевую ячейку «Затраты» вводим формулу: =СУММПРОИЗВ(Эксплут_затраты;План);
Запускаем программу Поиск решений командой Данные/Анализ/Поиск решения (В Excel 2007) Сервис/Поиск решения (В Excel 2003 и ниже). В полях Установить целевую ячейку, Изменяя ячейки, Ограничения вводим соответствующие адреса ячеек. Так как это линейная модель, то не забываем фиксировать в окне Параметры поиска решений переключатель на позицию Линейная модель и Неотрицательные значения. Нажимаем кнопку Выполнить и в появившемся окне Результаты поиска решения выводим отчет по устойчивости.
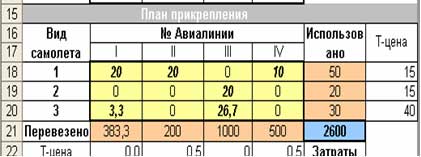
Анализ результатов.
При найденном плане прикрепления наши затраты будут минимальными в размере 2600 д. ед.
Теневые цены на количество самолетов указывают на увеличение общих затрат на перевозку если мы задействуем 1 дополнительный самолет. Теневые цены на план перевозок указывают на увеличение общих затрат при увеличение соответствующего плана на 1 ед.
Нормированные стоимости неизвестных (план прикрепления) указывают на увеличение общих затрат при принудительном использование «невыгодного» самолета на «невыгодной» авиалинии.
После анализа добавляем ограничения: План – целые числа.
Х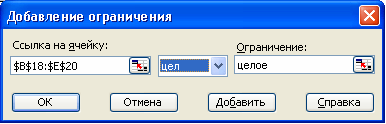
отя
общие затраты не возросли (1600), но
неизвестные плана стали целыми числами,
что естественно для самолетов, которые
нельзя поделить на части.
Задача на оптимальное распределение ресурсов
Постановка задачи.
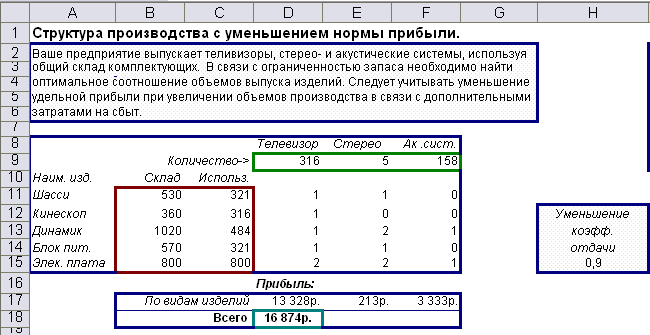
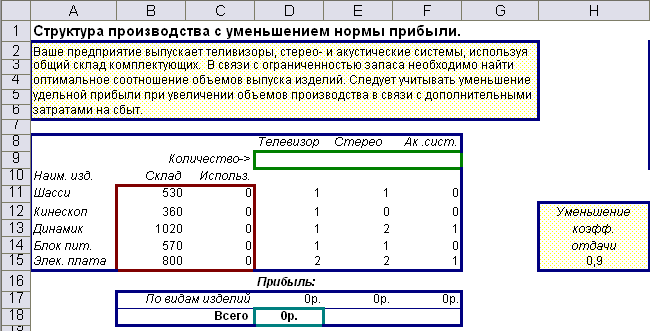
Суть задачи заключается в нахождении оптимального сочетания объемов производства телевизоров, стереосистем и акустических систем в условиях ограничений по числу комплектующих, причем одни и те же комплектующие используются в изделиях всех трех типов. Необходимо найти такие объемы производства изделий, чтобы комплектующие использовались наиболее оптимально.
Экономико-математическая модель
Целевой функцией является максимизация прибыли.
Изменяемые данные – количество выпускаемых изделий каждого вида.
Количество используемых комплектующих не должно превышать их запаса на складе.
Известно, сколько комплектующих каждого типа необходимо для выпуска единицы продукции соответствующего вида.
Количество выпускаемых единиц продукции любого типа должно быть больше нуля или равно нулю (очевидно, что объем выпуска не должен быть отрицательным).
Замечание ________________________________________________________________
Кстати, в подобных моделях возможно и указание некоторого неотрицательного числа — то есть, например, при оптимальном решении завод должен выпустить как минимум один телевизор, одну акустическую и стереосистему (это еще одно ограничение). Такие ограничения достаточно часто встречаются в реальной жизни. Например, найденое числовое оптимальное решение рекомендует вообще не выпускать продукцию одного или нескольких типов, однако качественные соображения целесообразности поддержания ассортиментного разнообразия требуют всё же выпускать менее рентабельную продукцию в каких-то объемах.
________________________________________________________________
Интересной особенностью этой модели является наличие коэффициента отдачи. Этот коэффициент (предполагается, что он найден эмпирическим путем из предыдущей статистики работы этого производства) отражает тот факт, что с увеличением объемов производства норма прибыли снижается. С математической точки зрения наличие этого коэффициента интересно том, что если он имеет значение меньше единицы, то это вносит в данную модель «нелинейность».
Реализация в Excel
Запускаем программу Поиск решений командой Данные/Анализ/Поиск решения (В Excel 2007) Сервис/Поиск решения (В Excel 2003 и ниже). В полях Установить целевую ячейку, Изменяя ячейки, Ограничения вводим соответствующие адреса ячеек. Так как это линейная модель, то не забываем фиксировать в окне Параметры поиска решений переключатель на позицию Неотрицательные значения. Нажимаем кнопку Выполнить.
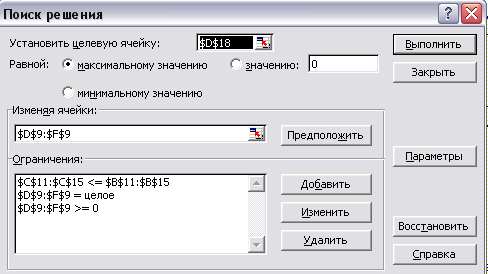
Результат.
