1. Что такое «стационарный режим процесса гибели и размножения».

С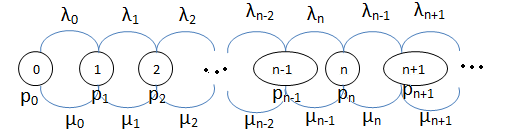 тационарный режим - это режим который описывается след. Графом:

Причем p_i=const.

2. Как связаны между собой вероятности n-ого и (n+1)-ого состояний процесса гибели и размножения в стационарном режиме.

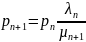
3. Запишите условие эргодичности процесса гибели и размножения.

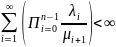
P₀>0

4. Задана СМО M/M/2/2. Как найти вероятность немедленного обслуживания?

5. Задана СМО M/M/3/2. Как найти вероятность ожидания?

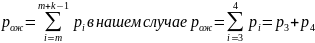
6. Задана СМО M/M/2/3. Как найти вероятность отказа?

7. Предмет исследования теории игр. Предметом исследования теории игр являются игры (конфликтные ситуации, в которой участвуют по крайней мере 2 стороны). Это изучение оптимальных стратегий игр.

8. Дайте определение игры. Игрой будем называть конфликтную ситуацию, в которой участвуют хотя бы 2 стороны (2 игрока).

9. Что такое партия? Партия – розыгрыш игры от начала до конца.

10. Что такое ход? Какими бывают ходы? Выбор и осуществление одного из действий¸ предусмотренных правилами игры, называют ходом игрока. Виды:

• Личный ход – осознанный выбор одного из возможных действий.

• Случайный ход – случайный выбор одного из возможных вариантов.

11. Что такое стратегия игрока? Стратегия – совокупность действий игрока, предусматривая его личный ход в каждой возможной ситуации, которая может сложиться в процессе игры.

12. Какая игра называется антагонистической? Антагонистической игрой называется некооперативная игра, в которой участвуют два игрока, выигрыши которых противоположны.

Или: антагонистической игрой называется игра если сумма платежей равна нулю.

13. Какая игра называется неантагонистической? Неантагонистической игрой называется игра если сумма платежей не равна нулю.

14. Что такое «игра с нулевой суммой»? Парная игра называется с нулевой суммой или если сумма платежей равна нулю. Игры с нулевой суммой — особая разновидность игр с постоянной суммой, то есть таких, где игроки не могут увеличить или уменьшить имеющиеся ресурсы, или фонд игры. В этом случае сумма всех выигрышей равна сумме всех проигрышей при любом ходе. Примерами таких игр может служить покер либо банальное воровство.

15. В каком случае возможна игра с ненулевой суммой? В играх с ненулевой суммой выигрыш какого-то игрока не обязательно означает проигрыш другого, и наоборот. Исход такой игры может быть меньше или больше нуля. Такие игры могут быть преобразованы к нулевой сумме — это делается введением фиктивного игрока, который «присваивает себе» излишек или восполняет недостаток средств.

16. Что такое «коалиционная игра»? Игра, в которой игроки могут объединяться в группы, беря на себя некоторые обязательства перед другими игроками и координируя свои действия.

17. Какую цель преследует в игре первый игрок? Максимизировать свой минимально возможный выигрыш.

18. Что такое «нижняя цена игры»? Максимальный гарантированный выигрыш первого игрока при использовании i-й стратегии

19. Какую цель преследует в игре второй игрок? Минимизировать свой максимально возможный проигрыш

20. Что такое «верхняя цена игры»? Минимальный гарантированный проигрыш игрока В при использовании j-й стратегии.

21. Каким соотношением связаны нижняя и верхняя цена игры. Если игра имеет седловую точку, то нижняя и верхняя цены игры равны.

22. Что цена игры? Всегда ли она существует? Цена игры – это максимальный гарантированный выигрыш первого игрока или минимальный гарантированный проигрыш второго игрока.

Выигрыш, соответствующей оптимальному решению, называется ценой игры. Если цена игры равна нулю, значит, это справедливая игра, т. е. она в одинаковой мере выгодна пли невыгодна той и другой стороне.

23. Что такое «смешанная стратегия»? Смешанная стратегия - такая стратегия, в которой ,в отличие от чистой, игроку следует выбирать ту или иную стратегию с некоторой долей вероятности. В чистой стратегии вероятность ее выбора равна 1, а всех других 0. Смешанной стратегией игрока А называется применение чистых стратегий А₁, А₂, …, А_m c вероятностями u₁, u₂, …, u_m.

Обычно смешанную стратегию игрока обозначают как вектор: U = (u₁, u₂, …, u_m)

24. Как задать чистую стратегию при помощи смешанных стратегий? Смешанной стратегией игрока А называется применение чистых стратегий А1, А2, …, Аm c вероятностями u1, u2, …, um. Обычно смешанную стратегию игрока обозначают как вектор: U = (u1, u2, …, um)

Стратегии: А1, А2,Ai, …, Аm  u1=0, u2=0,ui=1, …, um=0

25. Что такое «оптимальная стратегия первого игрока»? Оптимальная стратегия первого игрока та, которая обеспечивает ему максимальный выигрыш.

26. Что такое «оптимальная стратегия второго игрока»? Оптимальная стратегия второго игрока та, которая обеспечивает ему минимальный проигрыш.

27. Что есть «цена игры» в усредненной игре? Всегда ли она существует? в среднем на одну партию будет приходиться нулевой выигрыш («цена этой игры будет равна нулю): первый игрок не будет ни выигрывать, ни проигрывать

28. Что такое «полезная стратегия игрока»? Чистая стратегия игрока, которая в оптимальной смешанной стратегии соответствует ненулевой вероятности.

29. Первый игрок использует свою оптимальную стратегию. В каком случае проигрыш второго игрока будет минимальным? Если он будет пользоваться только активными стратегиями.

30. Второй игрок использует свою оптимальную стратегию. В каком случае выигрыш первого будет меньше цены игры.

31. Геометрическая интерпретация игры (2*n). Как Вы понимаете, что такое L(θ, y₂)? Выигрыш первого игрока, если второй игрок использует свою чистую стратегию y2.

32. Геометрическая интерпретация игры (2*n). Какой геом. объект соответствует функции L(x₂,θ)при 0≤ θ≤1? Прямая.

33. Сведение игры к злп. Запишите целевую функцию задачи.

v->min(max)

34. Сведение игры к злп. Запишите I-ое ограничение задачи.

a_1iu₁+ a_2iu₂ + …+a_miu_m >=v

35. Сведение игры к злп. Пусть - оптимальное решение злп. Как найти оптимальную стратегию первого игрока?

u*=νp_i

1. Процесс гибели и размножения в установившемся режиме.

µ – интенсивность обслуживания λ – интенсивность поступающих заявок

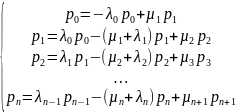
Для стационарного режима pi= const. Следовательно:

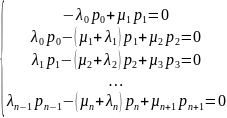
Отсюда поочередно выражая вероятности получим следующую обобщенную формулу:

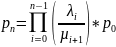
Между состояниями p_n и p_n-1 есть связь:

Исходя из того, что p₀+p₁+p₂+…=1 перейти к формуле:

Где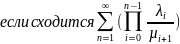 т.е <∞ при p>0 – условие эргодичности процесса гибели и размножения.

2. Исследование смо m/m/1.

λ_i=λ₁ i=0..∞ µ_j=µ₁ j=0..∞

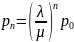
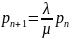
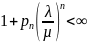- Условие эргодичности для данной системы

ρ- интенсивность использования СМО= max интенсивность поступления делить на max интенсивность обслуживания, тогда:

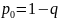или вероятность простоя отсюда:

Вероятность немедленного обслуживания:

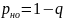
Вероятность ожидания:

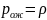
Отказы отсутствуют, так как система без отказов…

Среднее кол заявок в системе:

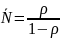
Среднее время пребывания заявки в системе:

3. Исследование смо m/m/m/k (на конкретном примере).

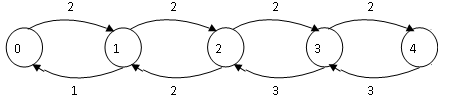
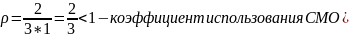
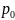- искомое

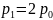
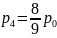
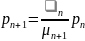
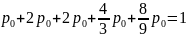
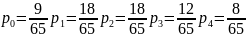
– вероятность немедленного обслуживания

– вероятность ожидания

– вероятность отказа

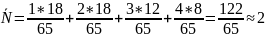– среднее количество заявок в системе

– средняя длина очереди

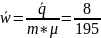– среднее время обслуживания

4. Формализованное описание игры. Ситуация наз. конфликтной, если в ней участвуют несколько сторон, интересы которых полностью или частично не совпадают, а, возможно, противоположны.

Игра – конфликтная ситуация, в которой участвуют по крайней мере 2 стороны. Допустимые действия каждого игрока, направленные на достижение его цели, наз. правилами игры. Игра наз. парной, если в ней участвуют ровно 2 игрока, и множественной, если больше.

Количественная оценка результата игры наз. платежом.

Парная игра наз. игрой с нулевой суммой (антагонистической), если сумма платежей равно нулю.

Любая игра состоит из последовательности ходов. Выбор и осуществление одного из действий, предусмотр. правилами игры, наз. ходом игрока. Ходы бывают личными(осознанный выбор игроком одного из действий) и случайными (случайный выбор одного из вариантов).

Партия – розыгрыш от начала и до конца.

Стратегия – совокупность действий игрока, предусматривающая его личный ход в каждой возможной ситуации, кот. может сложиться в процессе игры.

Игра наз. конечной, если у каждого игрока есть конечное число стратегий, и бесконечной, если это число бесконечно.

Стратегия игрока наз. оптимальной, если она обеспечивает игроку максимальный выигрыш при условии, что второй игрок тоже придерживается определённой стратегии.

Решить игру – найти оптимальные стратегии игроков.

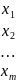стратегии игрока 1

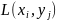– проигрыш/выигрыш

стратегии игрока 2

5. Пример построения матрицы игры 2-х лиц.

У 1-го игрока х_m – чистых стратегий, у 2-го - y_m.

L(x_i, y_i)= aij

Составим платежную матрицу:

А=

yi

aij – пересечение строки xi со столбцом yi.

6. Нижняя и верхняя цена игры, принципы максимина, минимакса. У 1-го игрока х_m – чистых стратегий, у 2-го - y_m. L(x_i, y_i)= aij Составим платежную матрицу:

А=

yi

игрок 1 выбрал стратегию i, тогда у него есть след. ряд: ai1, ai2, …, ain. Характеристикой i-ой стратегии игрока явл.:

1≤i≤m

α=max α_i= max min αij

1≤j≤m i j

α – назыв. нижней ценой игры, а стратегия 1-го игрока назыв. максиминой. Игрок 2 выбрал стратегию yi, тогда у него есть ряд: a1j, a2j, …, amj. В качестве проигрыша возьмем βj =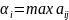 – максиминый проигрыш.

1≤i≤m

β=min β_i= min max αij

1≤j≤m 1≤j≤n 1≤i≤m

Стратегия 2-го игрока, найденного по этому правилу назыв. минимаксной.