
Лекція № 2. “поняття як форма абстрактного мислення”
Ключові слова.
2.1. Поняття
2.2. Зміст поняття
2.3. Обсяг поняття
2.4. Тотожність
2.5. Підпорядкування
2.6. Частковий збіг
2.7. Співпідпорядкування
2.8. Протилежність
2.9. Суперечність
Вхідна інформація.
Приступаючи до вивчення теми № 2, слід повторити попередню тему “Предмет і мова формальної логіки”.
2. Зміст теми.
Визначення поняття, його загальна характеристика.
Закон оберненого відношення між обсягом і змістом поняття.
Типи відношень між поняттями.
Визначення поняття, його загальна характеристика
Поняття (2.1.) є найпростішою формою теоретичного пізнання (мислення (1.1.)). Воно в загальному вигляді відбиває властивості предметів і явищ, відбиває (називає, позначає) предмети в їх вагомих сутнісних ознаках. Ознаками, у свою чергу, є певні властивості предметів, завдяки яким вони є подібними чи відрізняються.
2.1. Поняття – логічна форма мислення, що відображає предмети в їх суттєвих ознаках. |
Мовним еквівалентом поняття взагалі є окреме слово або словосполучення, що вказує на якийсь один предмет, їх окремий клас, певну ознаку предмета, наприклад: “викладач”, “маркетолог”, “фінансист”, “релігія”, “кандидат у майстри спорту”, “добрий”, “розумний”, “цінні папери”, “закон”, “формальний лідер” тощо. Разом з цим наука більш схильна розглядати у якості понять теоретичні інструментарії мови – терміни, які доведені до певної раціональної досконалості, завершеності, наприклад “есенція”, “демократія”, “тиранія”, “охлократія”, “громадянська суспільство” тощо.
Поняття (слова та словосполучення) утворюються шляхом таких розумових процесів:
аналіз – розумове розчленування предметів на складові, виділення в предметі окремих властивостей (при цьому кожний отриманий компонент і окрема якість називається окремим словом-поняттям);
синтез – зворотній процес об’єднання складових предмета у ціле;
порівняння – встановлення подібності або розбіжності предметів за суттєвими чи несуттєвими ознаками;
абстрагування – виділення в предметі певних суттєвих ознак – при цьому увага від несуттєвих відвертається;
узагальнення – розумове об’єднання окремих предметів у певне поняття.
Перераховані вище логічні прийоми використовуються при формуванні нових понять як у науковій діяльності, так і при опануванні знаннями в процесі навчання.
2.2. Закон оберненого відношення між обсягом і змістом поняття
Логіка встановлює дві базові найважливіші параметральні характеристики поняття – його обсяг (2.3) і зміст (2.2.).
Обсяг поняття означає сукупність предметів, які узагальнюються під даним поняттям. Іншими словами об’єм – це клас (кількість) предметів, які мисляться під даним поняттям.
2.3. Обсяг поняття – сукупність предметів, кожної яких притаманні суттєві ознаки. |
Зміст поняття – це сукупність суттєвих властивостей, які притаманні відображеному у даному понятті класу предметів.
2.2. Зміст поняття – сукупність суттєвих ознак предмета. |
Відношення між обсягом і змістом поняття регулює закон оберненого відношення (вперше сформульований в XVII ст. в логіці Пор-Рояля): чим ширший зміст поняття, тим вужчий його обсяг, і навпаки. Точніше, якщо зміст одного поняття є ширшим, ніж зміст іншого поняття, то обсяг першого поняття є вужчим, ніж обсяг другого поняття. Зазначимо, що в законі оберненого відношення йдеться про відношення між обсягом і змістом таких понять, що мають один і той самий рід.
Проілюструємо дію цього закону. Зміст поняття “студент” визначається ознакою “навчатись у вищому або середньому спеціальному учбовому закладі”. Обсяг цього поняття складає множина всіх людей, які навчаються у вузах і середніх спеціальних учбових закладах. Збільшимо зміст цього поняття (введемо нову ознаку): “навчатись на юридичному факультеті”. Таке збільшення змісту спричинить появу поняття з меншим обсягом (“студент-юрист”) позаяк буде матись на увазі лише множина студентів, що навчаються на юридичному факультеті.
Формулювання закону оберненого відношення спричинює проблему тлумачення оцінок “бути ширшим” і “бути вужчим ” стосовно обсягу і змісту понять.
У традиційній логіці вважалось, що характеристики “бути ширшим” і “бути вужчим ” означають: по відношенню до ознак – їх кількість, по відношенню до обсягу – кількість предметів, що складають обсяг того чи іншого поняття. Таке тлумачення дійсне стосовно вищезгаданого прикладу – ілюстрації, але існують випадки, які не підпадають під зазначене тлумачення.
По-перше, число ознак не завжди можливо точно підрахувати. Що можна сказати про кількість ознак у випадках:
(А) “ число, що ділиться (без остачі) на 2”;
(Б) “ число, що ділиться (без остачі) на 3 і на 2”;
(В) “ число, що ділиться (без остачі) на 3 або на 2 ”?
Можна говорити, що у випадку (А) маємо одну ознаку, а у випадках (Б-В) – дві ознаки; але можна також стверджувати наявність у всіх трьох випадках однієї ознаки із застереженням про наявність у випадках (Б-В) однієї складної ознаки.
По-друге, ознаки можуть суттєво відрізнятись за інформативністю. Наприклад,
(Г) “ людина, що знає всі живі європейські мови ” ;
(Д) “ людина, що знає англійську мову ”;
(Е) “ людина, що знає якусь з живих європейських мов ”.
У всіх трьох випадках начебто наявна одна (за кількістю) ознака. Але очевидно, що за обсягом ці поняття не є тотожними.
По-третє, інколи просто неможливо оперувати оцінками “ більше/менше”. Наприклад,
(Є) “ чотирикутник, що є квадратом ”;
(Ж) “чотирикутник, що є прямокутником ”.
Безглуздо запитувати про кількість квадратів і прямокутників. Про обсяг поняття “ чотирикутник, що є квадратом ” говоримо, що він є вужчим, ніж обсяг поняття “ чотирикутник, що є прямокутником ” не тому що квадратів менше, ніж прямокутників, а тому що всякий квадрат є прямокутником, але не навпаки (не всякий прямокутник є квадратом).
Схематично відношення між обсягом цих понять можна зобразити:

Отже, висловлювання “ поняття (Є) є вужчим за обсягом, ніж поняття (Ж)” означає лише відношення включення обсягу поняття (Є) в обсяг поняття (Ж). Тобто, кожен елемент обсягу поняття (Є) є водночас елементом обсягу поняття (Ж), але не навпаки (не кожний елемент обсягу поняття (Ж) є елементом обсягу поняття (Є)).
На підставі закону оберненого відношення зміст поняття (Є) повинен бути ширшим, ніж зміст поняття (Ж). Висловлювання “ поняття (Є) є ширшим за змістом, ніж поняття (Ж)” означає можливість логічного виведення змісту поняття (Ж) із змісту поняття (Є).
Дійсно, із змісту ознаки “ бути квадратом ” випливає ознака “ бути прямокутником ” але не навпаки.
Відношення між обсягами понять (А), (Б) і (В):
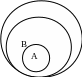
При побудові схеми відношень між обсягами цих понять неможливо керуватись критерієм кількості тих чи інших чисел. Керуємось іншими критеріями: кожне число, що ділиться (без остачі) на 3 і на 2 ділиться (без остачі) на 3, а також ділиться (без остачі) на 3 або на 2 (але не навпаки); кожне число, що ділиться (без остачі) на З ділиться (без остачі) також на 3 або 2 (але не навпаки). Відповідно, кожний елемент множини (Б) є елементом множини (А) і множини (В) (але не навпаки) і кожний елемент множини (А) є елементом множини (В), але не навпаки. Отже, поняття (Б) за обсягом є найвужчим, а за змістом - найширшим; поняття (В) за обсягом є найширшим, а за змістом - найвужчим.
Значення закону оберненого відношення між обсягом і змістом поняття полягає в тому, що цей закон відіграє важливу роль в аналізі відношень між поняттями, а також у логічних операціях узагальнення і обмеження понять.
