
- •Випадковий процес.
- •Переріз випадково процесу.
- •Траєкторія випадкового процесу.
- •Функція розподілу випадкового процесу.
- •Сімейство скінченновимірних розподілів випадкового процесу.
- •Теорема Колмогорова про існування випадкових процесів.
- •Основні класи випадкових процесів.
- •Математичне сподівання випадкового процесу.
- •Властивості математичного сподівання випадкового процесу.
- •Дисперсія випадкового процесу.
- •Властивості дисперсії випадкового процесу.
- •Центрована випадкова функція
- •39 Властивості нормованої кореляційної функції аналогічні властивостям кореляційної функції.
Випадковий процес.
Переріз випадкового процесу.
Траєкторія випадкового процесу.
Функція розподілу випадкового процесу.
Сімейство скінченновимірних розподілів випадкового процесу.
Теорема Колмогорова про існування випадкових процесів.
Основні класи випадкових процесів.
Математичне сподівання випадкового процесу.
Властивості математичного сподівання випадкового процесу.
Дисперсія випадкового процесу.
Властивості дисперсії випадкового процесу.
Центрований випадкова функція.
Кореляційна функція випадкового процесу.
Властивості кореляційної функції випадкового процесу.
Нормована кореляційна функція.
Властивості нормованої кореляційної функції.
Взаємна кореляційна функція двох випадкових процесів.
Властивості взаємної кореляційної функції двох випадкових процесів
Математичне сподівання суми випадкового процесу та випадкової величини.
Кореляційна функція суми двох корельованих випадкових процесів.
Кореляційна функція суми двох некорельованих випадкових процесів.
Границя в середньоквадратичному.
Похідна випадкового процесу.
Інтеграл випадкового процесу.
Математичне сподівання похідної випадкового процесу.
Кореляційна функція похідної випадкового процесу.
Взаємна кореляційна функція випадкового процесу та його похідної.
Математичне сподівання
 .
.Кореляційна функція .
Взаємна кореляційна функція випадкового процесу
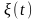 та
.
та
.Стаціонарно зв’язані випадкові процеси.
Стаціонарний випадковий процес у широкому розумінні.
Стаціонарний випадковий процес у вузькому розумінні.
Математичне сподівання стаціонарного випадкового процесу.
Дисперсія стаціонарного випадкового процесу.
Кореляційна функція стаціонарного випадкового процесу.
Властивості кореляційної функції стаціонарної випадкового процесу.
Нормована кореляційна функція стаціонарного випадкового процесу.
Властивості нормованої кореляційної функції стаціонарної випадкового процесу.
Взаємна кореляційна функція двох стаціонарних випадкових процесів.
Стаціонарно зв’язані випадкові процеси.
Математичне сподівання похідної стаціонарної випадкового процесу.
Кореляційна функція похідної стаціонарної випадкового процесу.
Взаємна кореляційна функція стаціонарної випадкового процесу та його похідної.
Кореляційна функція , де - стаціонарний випадковий процес.
Дисперсія , де - стаціонарний випадковий процес.
Взаємна кореляційна функція стаціонарної випадкового процесу та .
Випадковий процес.
Нехай є деякий ймовірнісний простір {Ω, B, P}, Ω - простір елементарних подій, В – сигма-алгебра, та деяка числова множина Т. Випадковий процес ʂ(t) називається параметричне сімейство випадкових величин {ʂ(t, w)}, де t є T, w є Ω. Випадковий процес – випадкова функція, де t відіграє роль часу.
Переріз випадково процесу.
Переріз випадкового процесу ʂ(t) – це випадкова величина, що відповідає фіксованому аргументу випадковго процес.
Траєкторія випадкового процесу.
Реалізація випадкового процесу ʂ(t) – це невипадкова функція аргументу t, яку ми отримцємо в результатті випробування.
Функція розподілу випадкового процесу.
Функція розподылу випадкового процесу називається функція вигляду F(x) = P(ʂ < x) – ймовірність того, що випадкова величина ʂ приєме значення < x.
Сімейство скінченновимірних розподілів випадкового процесу.
Нехай ʂ(t) – випадковий процес, де t є Т. Нехай задано моменти часу t1 < t2 < .. < tk є Т. Відповідний набір випадкових величин для цих моментів часу ʂ(t1), ʂ(t2), … , ʂ(tk) має k-вимірну функцію розподілу F(x1, x2, …, xk, t1, t2, … , tk) = P{ ʂ(t1) < x1, ʂ(t2) < x2, … , ʂ(tk) < xk}
Сукупність усіх к-вимірних функцій розподілу для різних к=1,2,… та всіх можливих моментів часу назив. Сімейством скінченновимірних розподілів вип. процесу ʂ(t).
Теорема Колмогорова про існування випадкових процесів.
Нехай задано сімейство скінченно-вимірних розподілів F = {F(x1..xk,t1..tk} k>=1, xє R, tєT, i=1,k} , які задовольняють умовам узгодженості(властивості фунції розподілу). Тоді існує такий ймовірнісний простір, на якому заданий випадковий процес, сімейство скінченно-вимірних розподілів якого співпадає з F.
Основні класи випадкових процесів.
Випадковий процес X (t) називається процесом з дискретним часом, якщо система, в якій він відбувається, може змінювати свої стани лише в моменти t1, t2 , ... ,tn , ... дискретної множини часу. Область визначення такого процесу є дискретною множиною { t1, t2 , ... ,tn , ... }
Випадковий процес X (t) називається процесом з неперервним часом, якщо система, в якій він відбувається, може переходити зі стану в стан у будь-який момент часу t (при будь-якому значенні аргументу).
Випадковий процес X (t) називається процесом з неперервними станами, якщо його переріз в будь-який момент часу є не дискретною випадковою величиною, а неперервною.
Випадковий процес X (t) називається процесом з дискретними станами, якщо в кожен момент часу t його множина станів є скінченною або зліченною.
Математичне сподівання випадкового процесу.
Математичним сподіванням випадкового процесу X (t) називається невипадкова функція, m x(t) яка при кожному фіксованому аргументі t дорівнює математичному сподіванню перерізу даного випадкового процесу: m x(t) = M(X (t))
Властивості математичного сподівання випадкового процесу.
Використовуючи властивості математичного сподівання випадкової величини, можна отримати властивості математичного сподівання випадкової функції:
• математичне сподівання невипадкової функції ϕ (t) дорівнює самій невипадковій функції:
M (ϕ(t ))=ϕ(t );
• невипадковий множник можна виносити за знак математичного сподівання:
M(ϕ(t)X(t))= ϕ(t)M(X(t))= ϕ(t) m x(t)
• математичне сподівання суми двох випадкових функцій дорівнює сумі математичних сподівань:
M (X(t)+Y (t))= mx (t) + m y(t );
• M (X (t) +ϕ (t)) = M (X( t)) + M( ϕ (t)) = mx (t)+ϕ (t) де X (t) – випадкова функція, ϕ(t) – невипадкова функція.
• якщо при всіх значеннях аргументу t перетини випадкових процесів X (t) і Y(t) є незалежними випадковими величинами, то математичне сподівання добутку цих процесів дорівнює добутку їх математичних сподівань: M (X(t)*Y (t))= mx (t) * m y(t );
