77

Предварительные определения

Определение. Поверхность принадлежит классу , если в некоторой окрестности каждой точки она представляется уравнением , причем и функция непрерывна вместе со всеми производными до порядка включительно в упомянутой окрестности.

Определение. Поверхность называется кусочно-гладкой, если она состоит из конечного числа поверхностей класса .

Определение. Множество называется открытым, если все его точки – внутренние.

Определение. Множество называется связным, если две любые его точки можно соединить кусочно-гладкой кривой, лежащей в этом множестве. Определение. Связное открытое множество называется областью. Будем рассматривать лишь области с кусочно-гладкой границей. Если не оговаривается обратное, будем считать границу компактной.

Определение. Компактом называется замкнутое ограниченное множество.

Определение. Точка называется предельной точкой множества , если существует последовательность , такая что

Дифференциальные уравнения в частных

производных второго порядка эллиптического типа

§ 1. Определение эллиптического уравнения. Основные понятия

Эллиптическое уравнение. Рассмотрим дифференциальное уравнение второго порядка вида

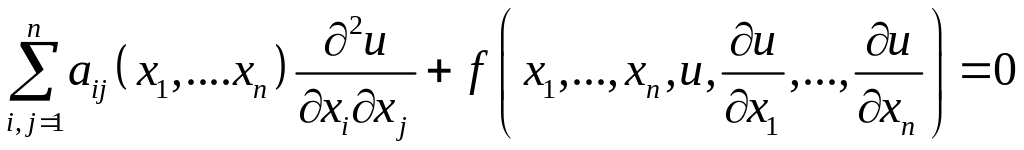. (1.1)

Это уравнение линейно относительно производных второго порядка. Главную роль в определении типа уравнения играют коэффициенты при старших производных. Будем считать, что аргументы этих функций имеют вид . Коэффициенты, не ограничивая общности, считаем симметричными: . Все функции и независимые переменные мы считаем вещественными.

Определение. Зафиксируем определенную точку в области и составим квадратичную форму

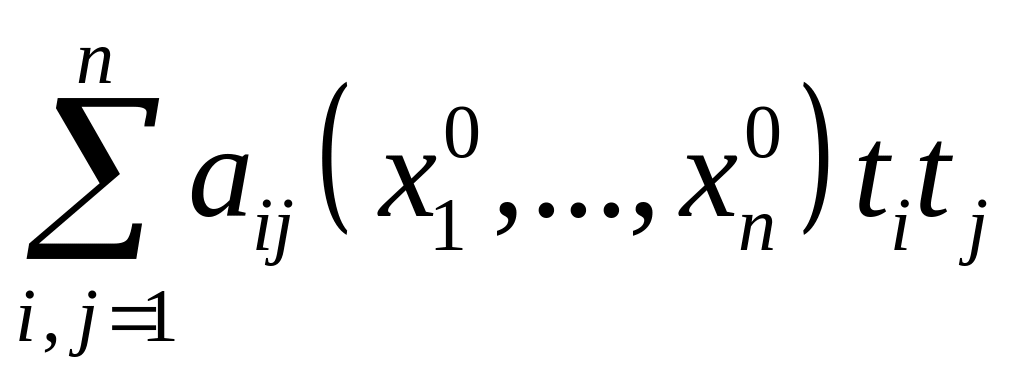. (1.2)

Уравнение (1.1) принадлежит эллиптическому типу в точке , если в этой точке квадратичная форма (1.2) знакоопределена.

Предположим, что коэффициенты - постоянные величины, тогда уравнение (1.1) имеет вид

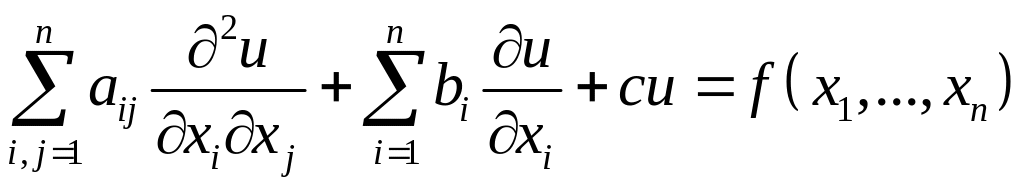, (1.3)

т.е. является линейным уравнением с постоянными коэффициентами.

В этом случае свойство знакоопределенности квадратичной формы (1.2) сохраняется вне зависимости от выбора точки . Предположим, что квадратичная форма (1.2) знакоопределена, т.е. уравнение (1.3) эллиптическое. При помощи линейного преобразования

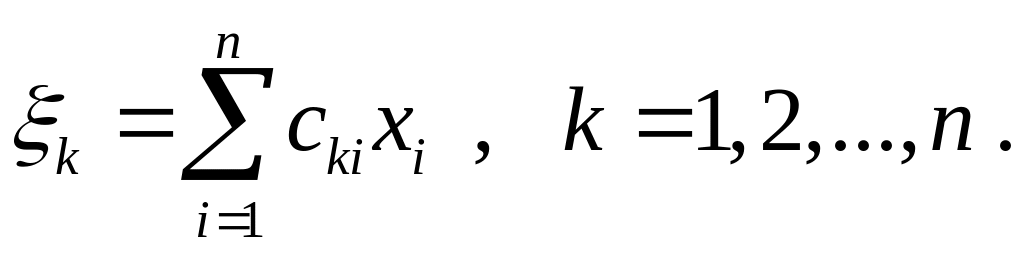(1.4)

ведем новые независимые переменные . Предположим, что преобразование (1.4) неособое, т.е. . Производные по старым переменным выразятся через производные по новым переменным следующим образом:

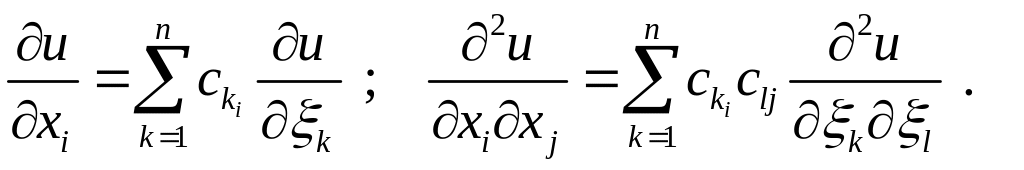(1.5)

Подставим представления (1.5) в уравнение (1.3), после чего получим новое уравнение

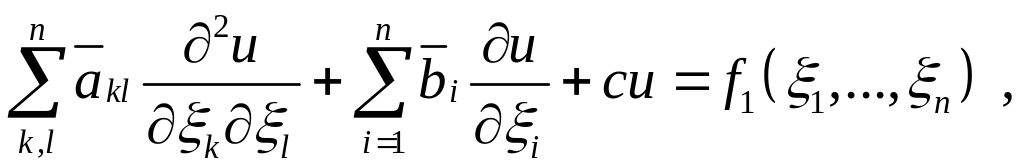(1.6)

где

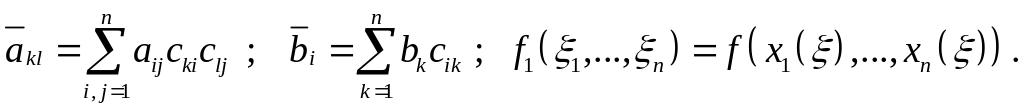(1.7)

Для того, чтобы понять, как преобразуются коэффициенты при старших производных, заметим, что при преобразовании квадратичной формы 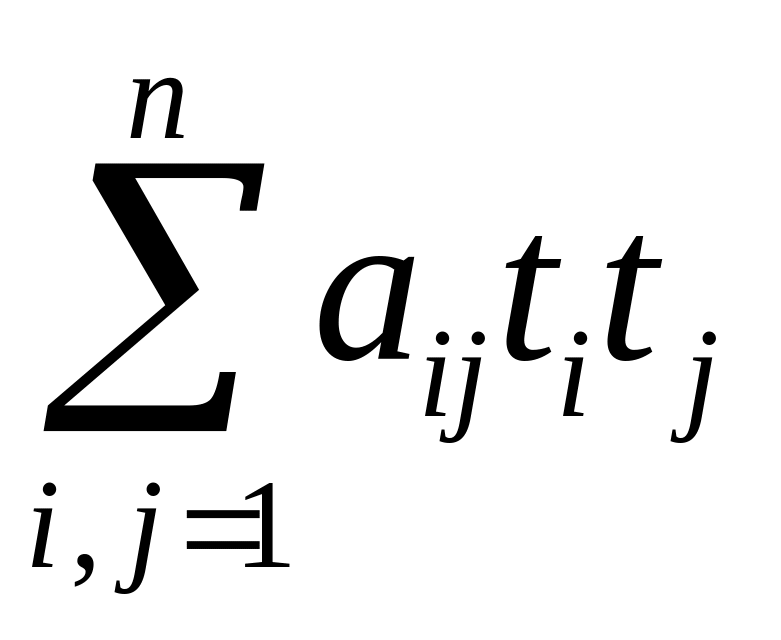с помощью линейного преобразования 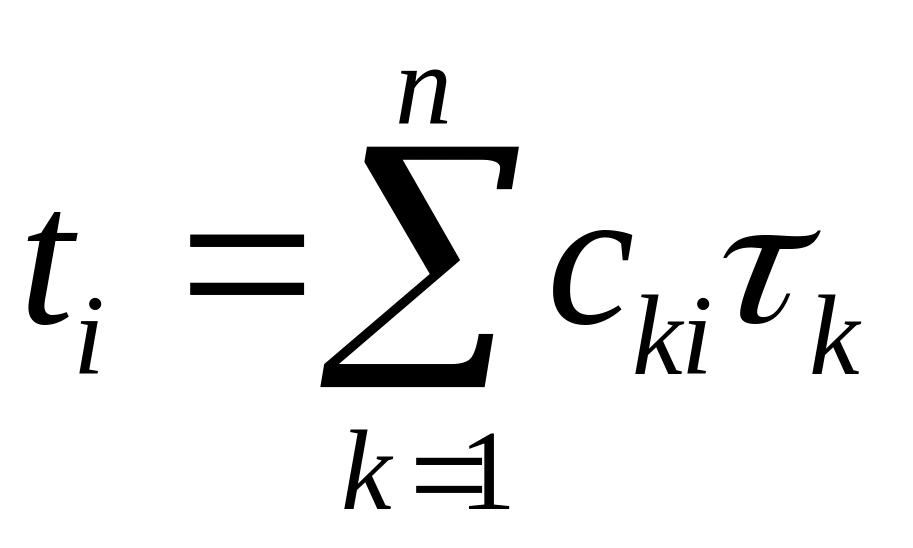, приводящего ее к виду 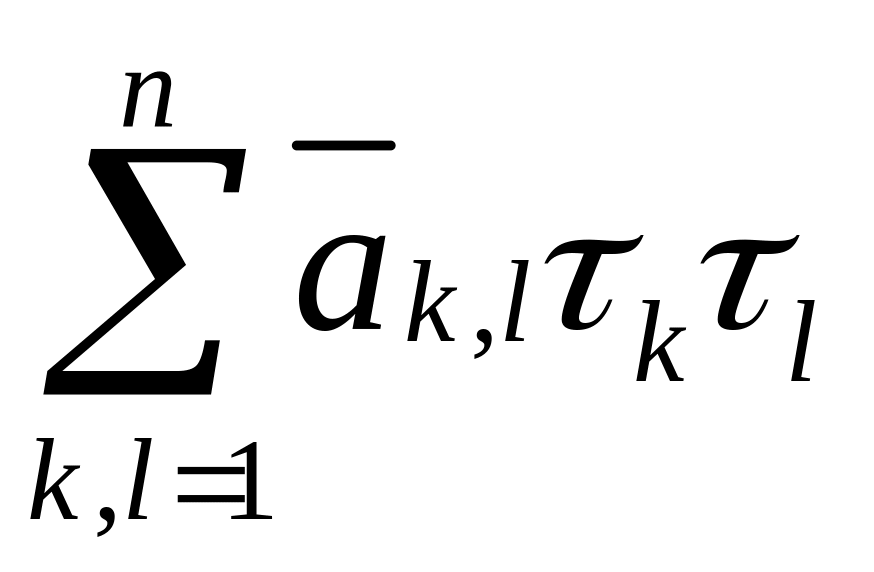, происходит та же замена коэффициентов. В алгебре доказывается (с помощью конструктивного метода выделения полных квадратов), что всегда можно подобрать коэффициенты так, чтобы квадратичная форма приводилась к сумме квадратов, т.е. к виду 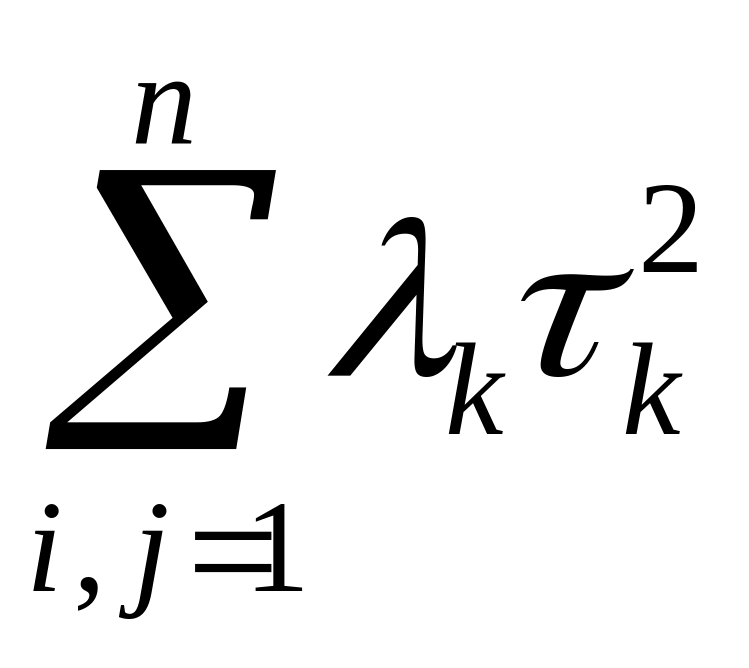, причем или 0. Согласно закону инерции число положительных и отрицательных коэффициентов инвариантно относительно выбора линейного преобразования . То же самое линейное преобразование можно использовать для преобразования аргументов в уравнении (1.3) в аргументы и, следовательно, для получения уравнения (1.6), которое с помощью замены координат можно представить в виде

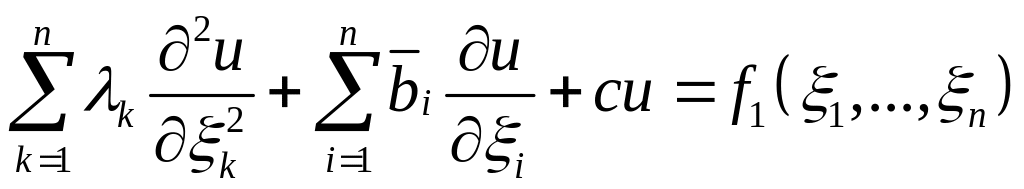. (1.8)

Этот вид уравнения (1.3) называется каноническим. В силу знакоопределенности для эллиптического уравнения (1.3) квадратичной формы , а, следовательно, и формы 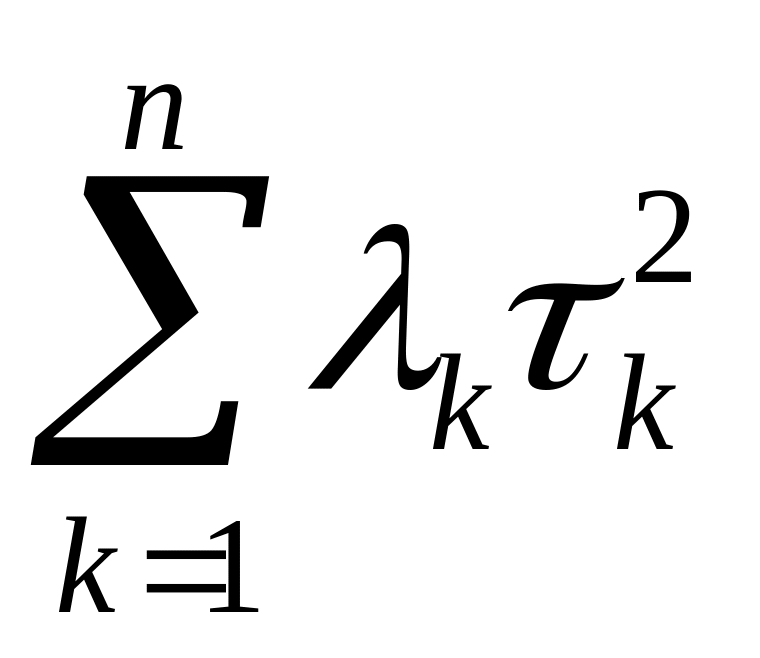, очевидно, что для эллиптического уравнения все равны единице: . Таким образом, сохраняя прежние обозначения, мы можем утверждать, что всякое линейное уравнение эллиптического типа с постоянными коэффициентами может быть приведено к виду

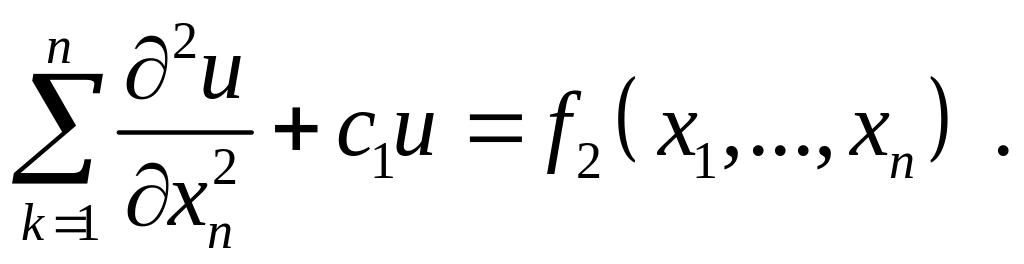
В случае, когда уравнение (1.1) имеет переменные коэффициенты, для каждой точки можно указать неособое преобразование независимых переменных, которое приводит уравнение (1.1) к каноническому виду. В случае двух независимых переменных возможно при весьма слабых условиях, налагаемых на коэффициенты при старших производных, привести уравнение с переменными коэффициентами к каноническому виду. Однако, это выходит за рамки нашего курса.

Уравнение Лапласа. К уравнениям эллиптического типа приводит изучение стационарных, т.е. не меняющихся с течением времени процессов различной физической природы. Простейшим уравнением эллиптического типа является уравнение Лапласа:

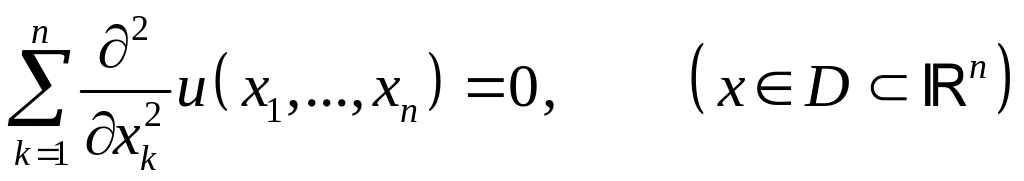; (1.9)

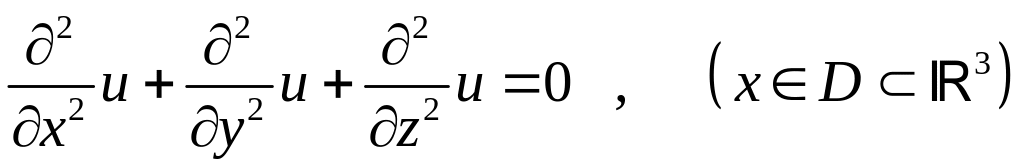. (1.10)

Уравнению Лапласа удовлетворяют установившаяся в однородном изотропном теле температура, среднее напряжение в твердом деформируемом теле, потенциалы поля тяготения и стационарного электрического поля.

Определение. Функция называется гармонической в ограниченной области , если она в этой области имеет все непрерывные частные производные до второго порядка включительно и удовлетворяет уравнению Лапласа.

Определение. Функция называется гармонической в области , имеющей выходы на бесконечность, если она в этой области имеет все непрерывные частные производные до второго порядка включительно, удовлетворяет уравнению Лапласа в и равномерно стремится к нулю при стремлении точки в бесконечность (функция при равномерно, если для любого можно указать так, что при .

Замечание. Предполагается, что граница области состоит из конечного числа замкнутых поверхностей.

Лемма 1. Пусть . Функция , где , является гармонической функцией переменной .

Доказательство проведем с помощью непосредственной проверки. Обозначим для удобства . Имеем

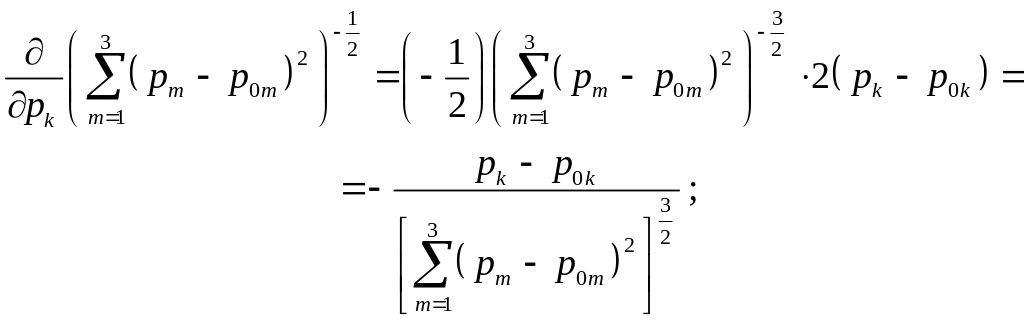
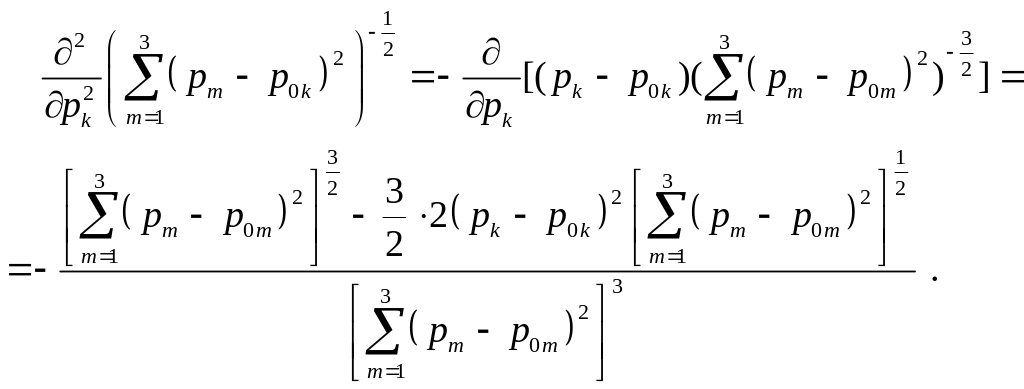
Отсюда

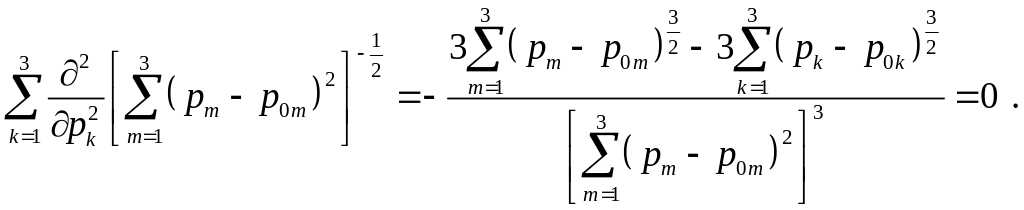
Лемма доказана.

Функция называется фундаментальным решением уравнения Лапласа (10) в .

Замечание. Пусть в уравнении (1.9) . Функция 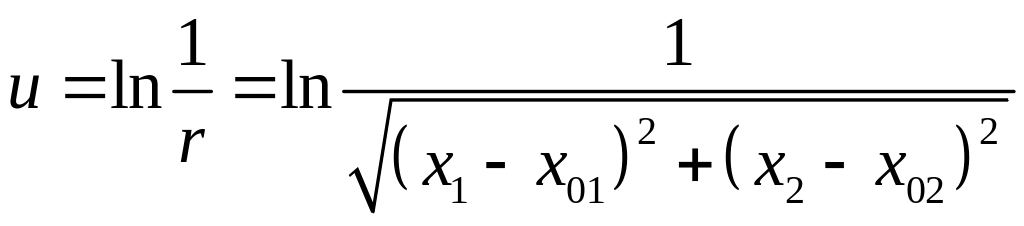является решением уравнения (1.9) при . Действительно,

;

;

.

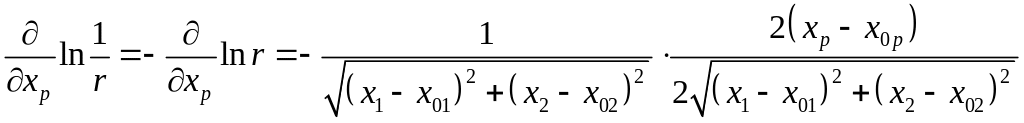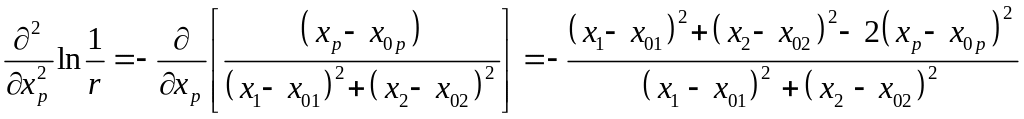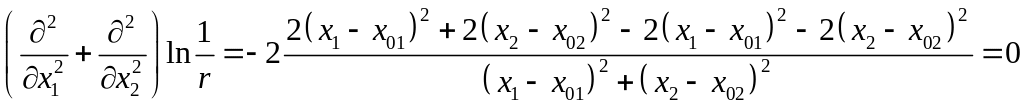Поэтому функцию называют фундаментальным решением уравнения Лапласа при .

Задание для самостоятельной работы. Доказать, что функция 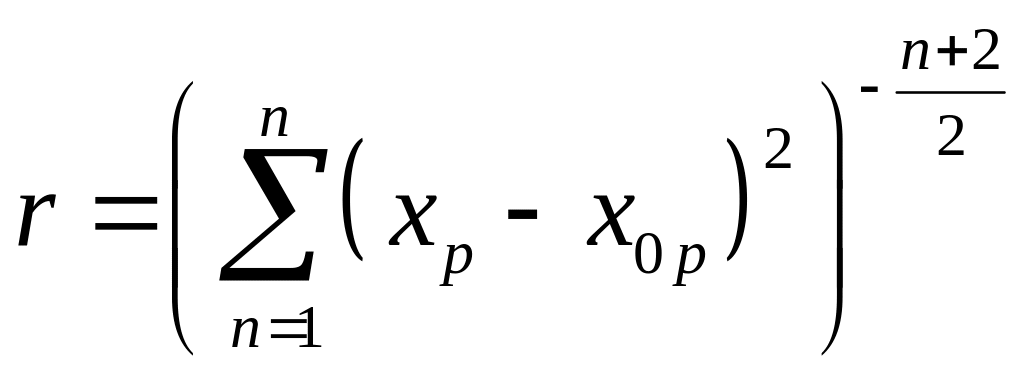при является решением уравнения (9) при всех .