Глава 6. Акустика залов

Принципиальное отличие звукового поля в закрытом помещении (зале) от свободного звукового поля состоит в том, что первое формируется не только прямым звуком от источника (или нескольких источников), но и большим числом звуковых волн, отраженных от внутренних ограждающих поверхностей (стен, потолка, пола) и предметов в помещении.

При этом нужно иметь в виду, что интенсивность каждого следующего отражения, приходящего в любую точку помещения, как правило, меньше предыдущего, во-первых, из-за частичного поглощения звука воздушным объемом помещения, а, во-вторых, из-за звукопоглощения материалами ограждающих поверхностей и предметов.

Для выявления акустических качеств помещений (залов) с речевыми и музыкальными программами недостаточно простого знания уровней силы звука (или звукового давления) в отдельные моменты времени на различных местах, а требуются еще и другие объективные физические характеристики звукового поля.

Они могут быть как интегральными, то есть характеризующими весь зал в целом, так и локальными, характеризующими отдельные слушательские места.

К первой категории можно отнести такие характеристики, как диффузность звукового поля и реверберация звука в зале, а ко второй – структуру звуковых отражений на слушательских местах.

Понятие диффузности звукового поля в замкнутом помещении (зале) кратко рассматривалось ранее (см. гл. 1, п.1.2.3).

Еще раз отметим, что идеально диффузное звуковое поле (со степенью диффузности  = 100%) практически невозможно получить ни в каком зале; можно лишь говорить о высокой степени диффузности (однородности и изотропности) звукового поля, да и то в дальней от источника звука зоне отраженных звуковых волн (где интенсивность прямого звука мала).

Приближенно эта область оценивается расстоянием от источника звука по формуле ,

где – средний коэффициент звукопоглощения в помещении, а S_огр – общая площадь ограждений.

Тем не менее для залов большого объема, с малым звукопоглощением, высокой степенью расчлененности ограждающих поверхностей (пилястры, кессоны) и наличием других структурных звукорассеивающих элементов (потолочные балки, колонны, барьеры балконов и лож, элементы декора) однородность звукового поля достаточно высока, чтобы имело смысл говорить о такой физической характеристике всего зала, как время реверберации.

6.1. Реверберация звука. Время реверберации

Явление реверберации («послезвучания») состоит в том, что после прекращения звучания источника звук в любой точке помещения не исчезает мгновенно, а ослабевает постепенно (пусть и достаточно быстро) до нуля (точнее, до уровня шумового фона).

Очевидно, это связано с тем, что даже после исчезновения прямого звука от источника в любую точку замкнутого помещения приходит практически бесконечная последовательность отраженных звуковых волн с постепенно убывающими амплитудами. Поэтому плотность звуковой энергии на любом слушательском месте (и сила звука) не падают мгновенно до нуля, а лишь постепенно убывают; причем быстрота убывания определяется общим звукопоглощением помещения.

К вопросу о реверберации звука в закрытом помещении (зале) можно подойти и с позиций волновой теории звука.

Известно, что любой воздушный объем помещения можно рассматривать как трехмерную колебательную систему с дискретным набором собственных частот колебаний («колебательных мод»). Для залов формы параллелепипеда их значения выражаются формулой

f_{к, n, m} = с₀/2 , (6.1)

где c₀ – cкорость звука в воздухе; к, n, m – натуральные числа (0, 1, 2, 3, 4 и т.д.); L, W и Н – размеры помещения.

Для залов большого объема в области средних и высоких частот эти колебательные моды так тесно расположены на частотной шкале, что их можно считать следующими непрерывно. Так что любой тон в сложном звуке источника найдет резонансный отклик в «лице» соответствующей моды колебаний воздушного столба – колебания соответственной частоты возбудятся. После прекращения звучания источника колебания воздушного объема начнут постепенно затухать из-за вязкого трения воздуха.

В рамках статистической (энергетической) теории акустики зала доказывается, что плотность звуковой энергии в любой точке помещения, а, следовательно, и сила звука должны после прекращения звучания источника затухать cо временем по экспоненциальному закону:

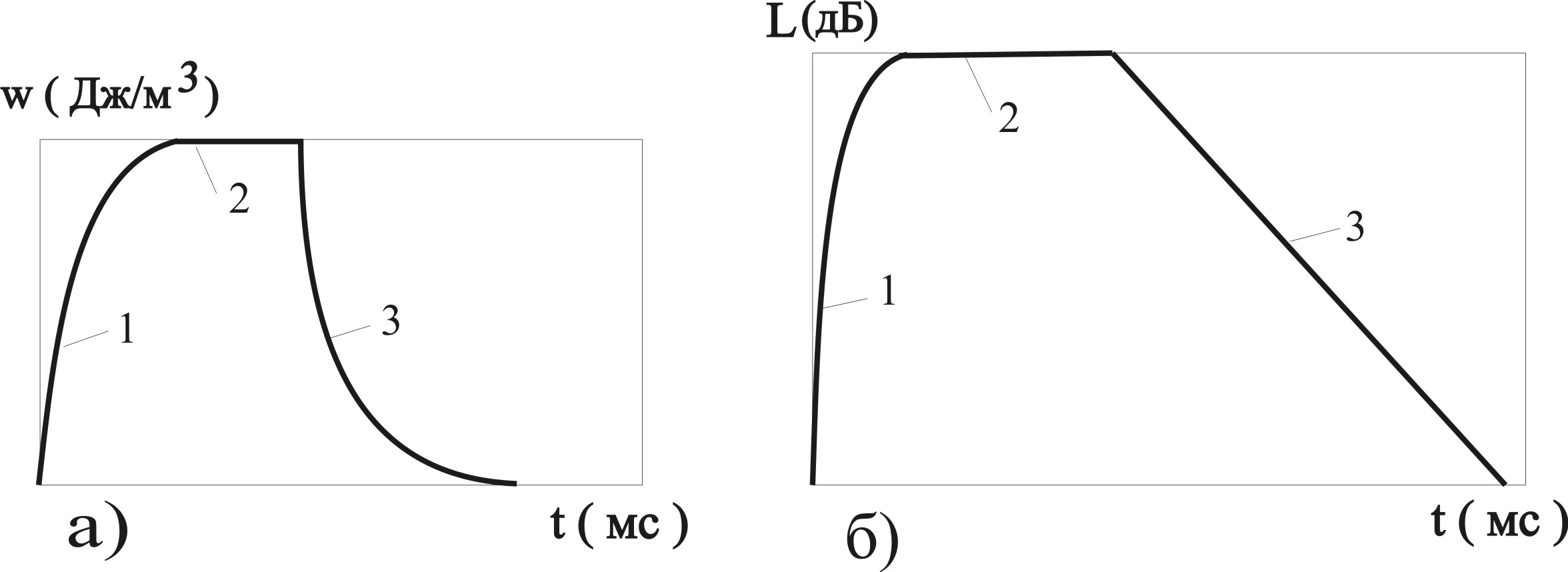
w = w₀ехр(–t), где  – коэффициент затухания; w₀ – стационарное значение объемной плотности энергии (рис. 6.1 а, кривая 3).

Если же говорить об уровне силы звука или уровне звукового давления L (в дБ), то их спад со временем (как логарифмических величин) должен тогда теоретически проходить по линейному закону (рис. 6.1 б, прямая 3).

Скорость спада со временем уровня звука L принято (по предложению американского акустика Сэбина) оценивать временем реверберации Т.

В качестве стандарта принято брать время Т, в течение которого плотность звуковой энергии w (и сила звука J) уменьшаются в миллион раз, а уровень звука L уменьшается на 60 дБ.

Рис. 6.1. Нарастание звука и реверберация в закрытом помещении:

а – изменение плотности звуковой энергии;

б – изменение уровня силы звука;

1 – процесс нарастания; 2 – стационарное состояние;

3 – реверберация звука

В предположении, что отражения звуков от ограждающих поверхностей помещения происходят непрерывно, Сэбин получил следующую простую формулу для стандартного времени реверберации:

. (6.2)

C учетом дискретности последовательных отражений звуков от ограждающих поверхностей формула (6.2) для времени реверберации несколько видоизменяется и заменяется более точной формулой Эйринга :

, (6.3)

где  ( ) = – ln (1– ) – функция Эйринга; V – объем помещения.

При малых значениях среднего коэффициента звукопоглощения (  0,2)

формулы (6.2) и (6.3) дают практически одинаковый результат.