35.Поняття графа, маршруту, ланцюга, дерева, циклу.

Графом G(V,E) назв. система, яка складається з двох множн: Verticas, Edges, вершина і ребра назив. інцедентними, якщо ця вершина є одним з кінців ребра.Скінченна послідовність суміжних ребер назив. маршрутом. Маршрут у якого всі ребра різні назив. ланцюгом. Ланцюг у якого всі вершини різні назив. постим ланцюгом. Граф назив. зв’язним якщо дві вершини можна з’єднати ланцюгом. Ланцюг у якого початкова і кінцева вершин збігаються назив. циклом. Звязнйграх, який немає циклів назив. деревом.

36.Властивості кривої Без'є.

1) вона є гладкою крвою; 2) вона починається в першій точці базового набору і завершується в останній. Всі інші базові точки, як правило не належать до кривої Без'є; 3) вона є дотичною до точок і кінцевого відрізка; 4) крива Без'є повністю лежить в середині базової опуклої оболонки. Для побудови кривої Без'є використовують кубічні сплайн:

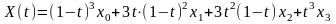
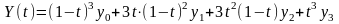
37. Алгоритм побудови карти щільності населення.

N населеня пунктів за допомогою плаваючих координат.

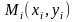і=1,N

Кількість жителів

Будуємо діаграму вороного для даної множини, визначимо площу кожного полігона 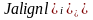визначити середню щільність населення для даного регіону

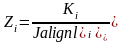
Співставляємо цю щільність з Будується регулярна модель мережі.

40.Алгоритм Пріма – Краскала, та його застосування.

1.Вибираємо ще нерозглянуте ребро мінімальної довжини.

2.Приєднуємо його до раніше вибраних ребер при умові що не утв. ціни.

3.Повторюємо №2 для всіх ребер.

Є декілька населених пунктів які треба зєднати мережею доріг. Побудувати оптимальну дорожну мережу у розумінні вартості. Вартість дороги прямо пропорційна її довжинію. Дана задача зводиться до побудови мінімального покриття графа, розвязок задачі дає алгоритм Пріма – Краскала.

41. Задача Пріма та алгоритм її розв'язування.

Є декілька населених пунктів, які треба зєднати мережею доріг.

На площу заданого N пунктів з координатами P1(x1, y1), … Pn(xn,yn). Необхідно спроектувати дорожню мережу(найкоротшу).

За критерій вибирається евклідова відстань:\

𝐷𝑖𝑗=𝑥𝑗−𝑥𝑖2+(𝑦𝑗−𝑦𝑖)^2

Алгоритм розвязку буде наступним:

1. Будуємо матрицю відстаней.

2. Використовуючи алгоритм Пріма-Краскала отримаємо мін покриваюче дерево.

Dij=sqrt((xj-xi)^2+(yj-yi)^2)

41. Поняття про розріз транспортної мережі. Теорема про мінімальний розріз.

Розрізом транспортної мережі наз.така множина Р вершин і дуг, які заходять у ці вершини, але не виходять з них. Причому t є Р, s є Р.

Теорема про мінімальний розріз:

Максимальна величина потоку, який можна пропустити через мережу = пропускній здатності мінімального розрізу.

41. Геометричний алгоритм побудови кривої Без'є.

1. Задані початкові вузлові точки Р0, Р1,Р2,Р3.

2. Вибирається параметр t, який 0<=t<=1. P0:(t=0); P3:(t=1).

3. Кожна сторона трикутника ділиться у відношенні до t .

4. Побудовані точки з’єднуємо.

5. Отримані відрізки ділимо у відношенні t, і т.д.

Алгоритм завершується коли отримаємо один відрізок.

Отримана точка належить кривій Без`є.