68. Алгоритм переходу від регулярної моделі рельєфу до моделі горизонталей.

У якості прикладу розглянемо алгоритм переходу від регулярної моделі висот до моделі горизонталей. Нехай задана регулярна модель рельєфу деякої квадратної ділянки території, кожна з комірок якої має вигляд квадрата із стороною 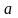. Математично дана модель представляється матрицею H_ij , i=1,n; j=1,m. Необхідно перейти від цієї моделі до картографічної моделі (моделі горизонталей). Для обрахунку координат точок, через які проходять горизонталі, використаємо лінійну інтерполяцію. Розглянемо одне з ребер комірки (рис.8). Нехай висоти у лівій та правій точках відрізка дорівнюють H₁ i H₂ відповідно. Необхідно знайти координату x точки, яка має висоту H₀ (H₁  H₀  H₂ , 0  x  a ).

x

a

H₁

H₀

H₂

Рис.8. Лінійне інтерполювання при побудові ізоліній висоти.

О

( 20 )

чевидно, що справедлива пропорція (H2 – H1) / a = (H0 – H1) / x. Звідси знаходимо координату x точки, що має висоту H₀ .

Тут X – шукана координата точки перетину, a – відстань між вузлами (за умовою - 10 м), H₁,H₂ – висоти двох сусідніх вузлів, H₀ – цілочисельне значення висоти горизонталі, причому або ж 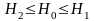. В окремих випадках, якщо цілі частини чисел 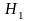і однакові, інтервал не перетинає жодна горизонталь.

29