11.Средняя линия треугольника.
Отрезок, соединяющий середины боковых сторон треугольника называется средней линией треугольника.
Свойство средней линии треугольника:
Средняя линия треугольника параллельна основанию треугольника и равна его половине.
12.Метрические соотношения в треугольнике:
Теорема
косинусов:
квадрат стороны треугольника равен
сумме квадратов двух других сторон без
удвоенного произведения этих сторон
на косинус угла между ними:
Теорема
синусов:
стороны треугольника пропорциональны
синусам противолежащих углов:
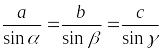
Обобщенная теорема синусов: отношение стороны треугольника к синусу противолежащего угла равно диаметру окружности, описанной около треугольника.
13.Свойства серединного перпендикуляра отрезка:
- Точка, лежащая на серединном перпендикуляре одинаково удалена от концов отрезка;
- любая точка, одинаково удаленная от концов отрезка, лежит на серединном перпендикуляре.
14.Окружность, описанная около треугольника:
- все три серединные перпендикуляры треугольника пересекаются в одной точке и эта точка является центром описанной окружности;
- около любого треугольника можно описать окружность и она единственна;
- центром окружности, описанной около правильного треугольника, является точка пересечения медиан, высот и биссектрис.
- центр окружности, описанной около равнобедренного треугольника, расположен на высоте, проведённой к основанию.
- центром окружности, описанной около прямоугольного треугольника, является середина гипотенузы.
-
Радиус окружности, описанной около
треугольника равен R=
или R=
-
Радиус окружности, описанной около
прямоугольного треугольника равен
половине гипотенузы R=
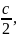
Вписанная в треугольник окружность:
- В любой треугольник можно вписать окружность и притом только одну.
- Центром вписанной в треугольник окружности является точка пересечения биссектрис треугольника.
-
Радиус вписанной в треугольник окружности
равен отношению площади треугольника
к полупериметру: r
=
,
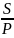- Радиус окружности, вписанной в прямоугольный треугольник с катетами a, b и гипотенузой c, равен r= (a+b −c)/2.
- Если M — точка касания окружности, вписанной в треугольник ABC со стороной AC, то AM = p −BC, где p — полупериметр треугольника.
- Окружность касается стороны BC треугольника ABC и продолжений сторон AB и AC. Тогда расстояние от вершины A до точки касания окружности с прямой AB равно полупериметру треугольника ABC.
-
Окружность, вписанная в треугольник
ABC, касается сторон AB, BC и AC соответственно
в точках K, L и M, тогда <KLM =90˚ −
.
Теорема Фалеса: Если на одной из двух прямых отложить равные отрезки и через их концы провести параллельные прямые, пересекающие вторую прямую, то на второй прямой отложатся равные между собой отрезки.
Обратная теорема: Если прямые, пересекающие стороны угла, высекают на них равные между собой отрезки, то эти прямые параллельны.
Теорема о пропорциональных отрезках: Параллельные прямые, пересекающие стороны угла, высекают на них пропорциональные отрезки.
Обратная теорема: Если прямые, пересекающие стороны угла, высекают на них пропорциональные отрезки, то эти прямые параллельны.