Планиметрия.

УГЛЫ

1.Два угла называются смежными, если у них одна сторона общая, а две другие являются дополнительными полупрямыми.

Свойство смежных углов: сумма смежных углов равна 180^°.

2.Два угла называются вертикальными, если стороны одного угла являются дополнительными полупрямыми сторон другого.

Свойство вертикальных углов: вертикальные углы равны.

3.Угол, равный 90^°, называется прямым углом. Прямые, пересекающиеся под прямым углом, называются перпендикулярными.

Через данную точку можно провести, и притом только одну, прямую перпендикулярную данной прямой.

4.Угол, меньший 90^°, называется острым. Угол больший 90^°, называется тупым.

5. Углы со взаимно параллельными сторонами равны, если они оба острые или оба тупые.

6. Углы со взаимно перпендикулярными сторонами равны или в сумме составляют 180º.

7. Углы со взаимно перпендикулярными сторонами равны, если они оба острые или оба тупые.

Теоремы о параллельных и перпендикулярных прямых:

1. Если параллельные прямые пересечены третьей прямой, то

- внутренние и внешние накрест лежащие углы равны,

- соответственные углы равны,

- внутренние и внешние односторонние углы в сумме равны 180^°;

2. Прямая, перпендикулярная одной из двух параллельных прямых, перпендикулярна и второй.

12. Признаки параллельности прямых.

- две прямые, параллельные третьей, параллельны между собой;

- если при пересечении двух прямых третьей, внутренние (внешние) накрест лежащие углы равны, то эти прямые параллельны;

- если при пересечении двух прямых третьей, внутренние (внешние) односторонние углы в сумме равны 180^°, то эти прямые параллельны;

- если при пересечении двух прямых третьей, соответственные углы равны, то эти прямые параллельны;

- две прямые, перпендикулярные одной и той же прямой – параллельны;

ТРЕУГОЛЬНИКИ.

1.Свойства сторон и углов треугольника:

- Неравенство треугольника: каждая сторона треугольника меньше суммы двух других его сторон и больше разности этих сторон.

Следствия из неравенства треугольника:

- сумма звеньев ломаной больше отрезка, соединяющего начало первого звена с концом последнего.

- против большего угла треугольника лежит большая сторона.

- против большей стороны треугольника лежит больший угол.

- гипотенуза прямоугольного треугольника больше катета.

- если из одной точки проведены к прямой перпендикуляр и наклонные, то

перпендикуляр короче наклонных;

- большей наклонной соответствует большая проекция и наоборот.

2.Сумма внутренних углов треугольника:

- сумма любых двух углов треугольника меньше 180^°;

- в каждом треугольнике два угла острые;

- сумма острых углов прямоугольного треугольника равна 90^°.

3.Внешним углом треугольника ABC при вершине A называется угол, смежный углу треугольника при вершине A.

- внешний угол треугольника больше любого внутреннего угла, не смежного с ним;

- внешний угол треугольника равен сумме двух внутренних углов, не смежных с ним.

4. Правильным или равносторонним называют треугольник, у которого все стороны равны.

Свойства правильного треугольника:

- в равностороннем треугольнике все углы равны по 60̊;

- в равностороннем треугольнике высоты являются медианами и биссектрисами;

- элементы равностороннего треугольника со стороной a:

пусть h, S, R, r — высота, площадь, радиусы описанной и вписанной окружностей равностороннего треугольника со стороной a. Тогда

h = , S = , R = , r =

5.Равнобедренным называют треугольник, у которого две стороны равны.

Свойства равнобедренного треугольника:

- в равнобедренном треугольнике углы при основании равны;

- в равнобедренном треугольнике медиана, проведенная к основанию, является биссектрисой и высотой;

Признаки равнобедренного треугольника:

- если в треугольнике два угла равны, то он равнобедренный;

- если медиана треугольника является его высотой, то треугольник равнобедренный.

- если биссектриса треугольника является его высотой, то треугольник равнобедренный.

- если медиана треугольника является его биссектрисой, то треугольник равнобедренный.

6. Прямоугольным называется треугольник, у которого есть прямой угол. Сторона, лежащая против прямого угла, называется гипотенузой. Стороны, образующие прямой угол, называются катетами.

Свойства сторон и углов прямоугольного треугольника:

- катет, лежащий против угла 30˚, равен половине гипотенузы;

- если катет прямоугольного треугольника равен половине гипотенузы, то угол, противолежащий этому катету, равен 30˚.

- углы, противолежащие катетам – острые;

- гипотенуза больше любого из катетов;

- сумма катетов больше гипотенузы;

- сумма острых углов прямоугольного треугольника равна 90^°.

Тригонометрические соотношения в прямоугольном треугольнике:

-синусом острого угла прямоугольного треугольника называется отношение противолежащего катета к гипотенузе. Синусы смежных углов равны.

-косинусом острого угла прямоугольного треугольника называется отношение прилежащего катета к гипотенузе. Косинусы смежных углов противоположны.

-тангенсом острого угла прямоугольного треугольника называется отношение противолежащего катета к прилежащему. Тангенсы смежных углов противоположны.

-котангенсом острого угла прямоугольного треугольника называется отношение прилежащего катета к противолежащему. Котангенсы смежных углов противоположны.

Решение прямоугольных треугольников:

- катет прямоугольного треугольника равен произведению гипотенузы на синус противолежащего или на косинус прилежащего к этому катету острого угла.

- катет прямоугольного треугольника равен другому катету, умноженному на тангенс противолежащего или котангенс прилежащего к этому катету острого угла.

-гипотенуза прямоугольного треугольника равна катету, поделённому на синус противолежащего или на косинус прилежащего к этому катету острого угла.

Теорема Пифагора: квадрат гипотенузы прямоугольного треугольника равен сумме квадратов катетов.

Теорема, обратная теореме Пифагора: если квадрат стороны треугольника равен сумме квадратов двух других его сторон, то этот треугольник — прямоугольный.

Пропорциональные отрезки в прямоугольном треугольнике:

- высота, проведенная из вершины прямого угла, есть среднее пропорциональное проекций катетов на гипотенузу, а каждый катет есть среднее пропорциональное гипотенузы и проекции этого катета на гипотенузу.

7.Равные треугольники.

Треугольники называются равными , если у них все углы и все стороны равны (при наложении они совпадают).

Признаки равенства треугольников:

- Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то треугольники равны.

- Если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то треугольники равны.

- Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то треугольники равны.

Признаки равенства прямоугольных треугольников:

• если катет и острый угол одного треугольника равны катету и острому углу другого треугольника, то треугольники равны;

• если два катета одного треугольника равны двум катетам другого треугольника, то треугольники равны;

• если катет и гипотенуза одного треугольника равны катету и гипотенузе другого треугольника, то треугольники равны;

• если гипотенуза и острый угол одного треугольника равны гипотенузе и острому углу другого треугольника, то треугольники равны.

Свойство равных треугольников:

В равных треугольниках против равных углов лежат равные стороны, а против равных сторон лежат равные углы.

8.Медианой треугольника называют отрезок, соединяющий вершину треугольника с серединой противоположной стороны.

Свойства медиан треугольника:

- три медианы треугольника пересекаются в одной точке, которая делит каждую медиану в отношении 2:1, считая от вершины треугольника;

- медиана делит треугольник на два равновеликих (равных по площади) треугольника;

- три медианы треугольника делят треугольник на шесть равновеликих треугольников.

Медиана прямоугольного треугольника

- медиана прямоугольного треугольника, проведенная из вершины прямого угла, равна половине гипотенузы.

- если медиана треугольника равна половине стороны, к которой она проведена, то треугольник прямоугольный.

Формула для медианы треугольника.

Если m — медиана треугольника, проведенная к стороне c, то = где a и b — две другие стороны треугольника.

Длина стороны треугольника через медианы выражается формулой:

9. Биссектрисой угла называют луч, делящий угол на два равных угла.

Биссектрисой треугольника называют отрезок биссектрисы угла треугольника,соединяющий вершину угла с точкой противоположной стороны.

Свойства биссектрисы:

- биссектрисы треугольника пересекаются в одной точке;

- любая точка, лежащая на биссектрисе угла, одинаково удалена от сторон угла;

- любая точка, одинаково удаленная от сторон угла, лежит на биссектрисе угла.

- биссектриса треугольника делит противолежащую сторону на отрезки, пропорциональные прилежащим сторонам треугольника.

- угол между биссектрисами смежных углов равен 90˚;

- биссектрисы внутренних односторонних углов при параллельных прямых и секущей перпендикулярны.

- Длина биссектрисы треугольника выражается формулой:

,

10.Высота треугольника – это перпендикуляр, опущенный из вершины треугольника на противоположную сторону или на ее продолжение.

Свойство высот треугольника:

- Три прямые, содержащие высоты треугольника, пересекаются в одной точке.

- Высоты треугольника обратно пропорциональны сторонам : : : 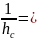a : b : c