3.2.2 Вычисление геометрических характеристик подобранного сечения
Фактическая площадь
равна конструктивной из предыдущего
пункта
.
Момент инерции в сечении относительно оси x:
;
(3.2.2.1)
.
Момент инерции в сечении относительно оси y:
;
(3.2.2.2)
.
Момент сопротивления относительно оси x:
;
(3.2.2.3)
.
Ядровое расстояние:
;
(3.2.2.4)
см.
Радиусы инерции:
;
(3.2.2.5)
см.
;
(3.2.2.6)
см.
Гибкости верхней части колонны:
;
(3.2.2.7)
.
;
(3.2.2.8)
.
3.2.3 Проверка устойчивости в плоскости действия изгибающего момента
Приведенная гибкость:
,
(3.3.1)
где
- модуль упругости стали, мПа.
.
Относительный эксцентриситет:
;
(3.3.2)
.
Соотношение площадей:
;
(3.3.3)
По таблице 2.1
источника [1] в зависимости от
,
и
принимаем коэффициент формы сечения:
,
(3.3.4)
где
=
1,52;
.
Приведенный эксцентриситет:
;
(3.3.5)
.
По таблице 1
приложения источника [1] в зависимости
от
определяется коэффициент
продольного изгиба при внецентренном
сжатии
0,263.
Проверка устойчивости:
;
(3.3.6)
.
Устойчивость в плоскости действия изгибающего момента обеспечена.
3.2.4 Проверка устойчивости из плоскости действия изгибающего момента
За расчетный изгибающий момент принимается больший из двух моментов. Наибольший изгибающий момент в пределах средней трети высоты надкрановой части:
;
(3.4.1)
;
;
(3.4.2)
.
Относительный эксцентриситет
,
(3.4.3)
где
- наибольший по абсолютной величине
момент из
и
,
;
м.
Определяем коэффициент с, учитывающий влияние изгибающего момента на устойчивость внецентренно сжатого стержня:
,
(3.4.4)
где
- коэффициенты, определяются по таблице
2.2 источника [1].
Находим значение
коэффициента
:
;
(3.4.5)
.
Коэффициент
определяем по формуле 3.4.6:
,
(3.4.6)
поскольку выполняется условие 3.4.7:
;
(3.4.7)
.
По таблице 2
приложения источника [1] определяем
и
как для
центрально-сжатого стержня в зависимости
от коэффициентов
и
:
,
.
Приведенная гибкость:
;
(3.4.8)
.
Проверка устойчивости:
;
(3.4.9)
.
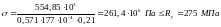Таким образом, устойчивость надкрановой части колонны обеспечена в плоскости и из плоскости действия изгибающего момента.
3.2.5 ПРОВЕРКА МЕСТНОЙ УСТОЙЧИВОСТИ
Проверяем устойчивость поясов колонны:
,
(3.5.1)
где
-
свес пояса, см;
Условие соблюдается, следовательно, устойчивость обеспечена.
Проверяем устойчивость стенки. Наибольшее напряжение сжатия на краю стенки:
;
(3.5.2)
Напряжения на противоположном краю стенки:
;
(3.5.3)
Таким образом, устойчивость стенки также обеспечена. Окончательно принимаем сечение надкрановой части колонны.
3.3 РАСЧЕТ ПОДКРАНОВОЙ ЧАСТИ КОЛОННЫ
3.3.1 ОПРЕДЕЛЕНИЕ РАСЧЕТНЫХ ПРОДОЛЬНЫХ УСИЛИЙ
Согласно правилу знаков изгибающих моментов, для наружной ветви наиболее невыгодна комбинация усилий в сечении 4-4, для подкрановой ветви – в сечении 3-3.
Поскольку
положительный момент
(догружающий
наружную ветвь) по абсолютному значению
примерно равен отрицательному моменту
,
смещение центра тяжести сечения
относительно середины колонны принимаем
равным нулю. Поэтому принимаем (рисунок
3.3.1.1):
Рисунок 3.3.1.1 – Сечение подкрановой части колонны
(3.3.1.1)
где
(3.3.1.2)
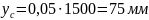
Тогда ориентировочное продольное усилие:
в подкрановой ветви
(3.3.1.3)
в наружной ветви
(3.3.1.4)
