9.6 Поняття про наближені методи розв’язування задач пружного режиму

Розв’язки будь-яких задач неусталеної фільтрації пружної рідини можна дістати добре розробленими методами математичної фізики. У розглянутих найпростіших випадках нескінченного пласта розв’язки включають інтеграл імовірностей чи інтегральну показникову функцію. У випадку обмеженого пласта, коли не можна нехтувати впливом меж, розв’язки отримуються у вигляді рядів Фур’є (прямолінійно-паралельна фільтрація) або Фур’є-Бесселя (плоско-радіальна фільтрація), які погано сходяться. Тому розроблялися наближені методи, серед яких можна виділити такі три групи.

До першої групи відносимо методи послідовної зміни стаціонарних станів (ПЗСС), А.М.Пірвердяна (МП) та інтегральних співвідношень (розроблено Г.І.Баренблаттом – МБ). Вони базуються на трьох припущеннях:

1) пласт поділяється на скінченну область збуреного руху й область незбуреного стану;

2) всередині збуреної області задається закон розподілу тиску, який зростає від тиску р_с (чи тиску р_г) до тиску р_к; у незбуреній області тиск усюди постійний і дорівнює тиску р_к;

3) розмір області збурення тиску визначається з додаткових умов стосовно до плоско-радіального потоку у вигляді:

, (9.119)

чи

Так, для прямолінійно-паралельного потоку у випадку заданого постійного об’ємного дебіту Q_o маємо:

, (9.123)

де об’єм збуреної зони пласта

(9.124)

і зміна тиску в цій зоні

(9.125)

- середній тиск у збуреній зоні (див. § 4.1).

Із рівняння (9.121) для за знаходимо

,

звідки

Тоді рівняння (9.123) записуємо так:

звідки довжина зони збурення тиску

(9.126)

Розподіл тиску в пласті на основі рівняння (9.121) описуємо формулою:

(9.127)

де причому за .

В іншому випадку, коли в момент часу t галерею пущено в роботу з постійним тиском , масовий дебіт галереї

(9.128)

де – густина рідини на стінці галереї.

Для прямолінійної епюри тиску маса відібраної рідини або, іншими словами, пружний масовий запас рідини

(9.129)

де добуток (див. § 9.1), а тоді

(9.130)

Тут – добуток коефіцієнта пористості і густини рідини відповідно за тисків .

Диференціюючи останній вираз по часу t і прирівнюючи з формулою масового дебіту, маємо

або припустивши, що ,

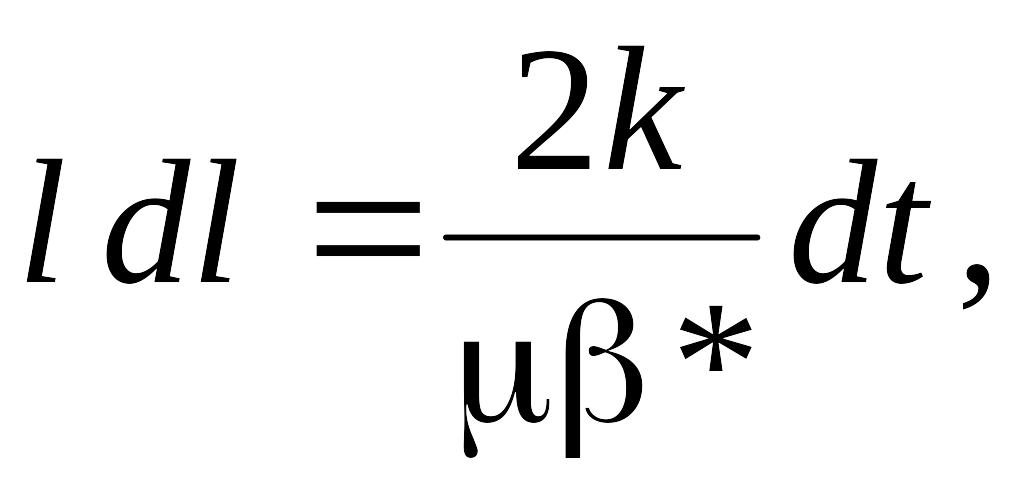
звідки отримуємо вираз довжини зони збурення тиску

(9.131)

Тоді записуємо рівняння розподілу тиску в пласті на основі формули (9.121)

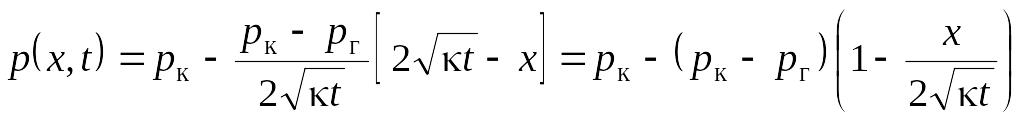(9.132)

і формулу дебіта галереї

(9.133)

У випадку плоско-радіального фільтраційного потоку пружної рідини до свердловини із заданим постійним об’ємним дебітом Q_о маємо:

(9.134)

де

(9.135)

(9.136)

(9.137)

Тоді знаходимо:

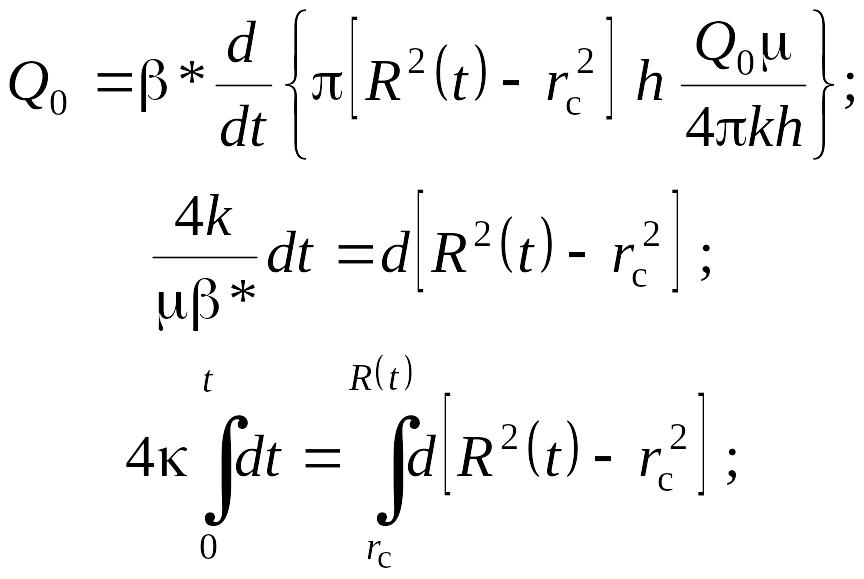
(9.138)

На основі формули (9.105) записуємо рівняння розподілу тиску в пласті:

(9.139)

і депресію тиску

(9.140)

причому за

в пласті.

За методом А.М.Пірвердяна розподіл тиску стосовно до прямолінійно-паралельного потоку задається у вигляді квадратичної параболи, що забезпечує плавне змикання профілів тиску в збуреній і незбуреній зонах:

, (9.141)

де

Із рівняння (9.141) знаходимо величину градієнта тиску на стінці галереї тобто

(9.142)

а тоді з використанням рівняння (9.142) записуємо формулу дебіта галереї, який задаємо постійним:

(9.143)

Середній тиск у пласті

(9.144)

а тоді зниження тиску в пласті з використанням рівняння (9.143)

(9.145)

де

Підставляючи знайдені величини в рівняння матеріального балансу, отримуємо:

(9.146)

Розподіл тиску за заданого дебіту на основі рівняння (9.141) описується формулою:

(9.147)

а депресія тиску за

(9.148)

де за

В іншому випадку потоку до галереї, пущеної в роботу з постійним тиском , аналогічно знаходимо:

(9.149)

(9.150)

(9.151)

Підставляючи похідні від р по x чи по r із рівняння (9.152) чи (9.153) відповідно у рівняння (9.154) чи (9.155) та інтегруючи, одержують необхідні співвідношення для коефіцієнтів многочлена та для відстані чи радіуса .рівнянн

Покажемо застосування методу інтегральних співвідношень для розв’язування задачі неусталеної фільтрації до свердловини, пущеної в роботу в момент часу з постійним дебітом. Розподіл тиску в збуреній зоні пласта задаємо у вигляді многочлену першої степені (n = 2):

(9.156)

Для визначення коефіцієнтів задаємо умови:

а) на стінці свердловини (на вибої свердловини)

(9.157)

б) на межі збуреної області

; (9.158)

в) гладкості кривої розподілу тиску на межі області збурення

(9.159)

Відповідно із цих умов з використанням рівняння (9.153) знаходимо:

а тоді формула розподілу тиску набуває вигляду

(9.160)

Для знаходження необхідно використати рівняння матеріального балансу (див. вище), яке слідує із інтегрального співвідношення (9.155) за φ = 1, при цьому середній тиск у зоні збурення треба знайти інтегруванням як середньозважений по всьому об’єму збуреної зони (аналогічно як за методом А.М. Пірвердяна). Покажемо це. Знаходимо:

(9.161)

де нехтували виразами, що містять і внаслідок їх малої величини.

Формула розподілу тиску набуває вигляду:

(9.162)

а також формула депресії тиску, коли за ,

(9.163)

де

Відносна похибка обчислень депресії тиску порівняно з точним розв’язком становить – (3,2…4,9)% для параметра , тобто отримуємо занижені значини депресії тиску.

До другої групи відноситься метод “усереднення” Ю.Д. Соколова-Г.П. Гусейнова. Суть його полягає в тому, що похідна усереднюється по всій збуреній області і замінюється функцією часу, тобто

, (9.164)

де – об’єм збуреної області; .

Тоді диференціальне рівняння пружного режиму набуває вигляду:

(9.165)

тобто така заміна дає змогу спростити диференціальне рівняння і звести його інтегрування тільки по координаті r.

Робимо підстановку , тоді знаходимо:

(9.166)

де - постійні інтегрування.

Нехай свердловину пущено в роботу з постійним об’ємним дебітом Q₀. Тоді початкова і граничні умови мають вигляд:

(9.167)

Із першої умови знаходимо

а із другої умови

Тоді маємо формулу розподілу тиску:

аб

(9.168)

Із третьої умови знаходимо функцію , тобто

(9.169)

Підставляючи знайдений вираз у формулу розподілу тиску і нехтуючи членами з , маємо:

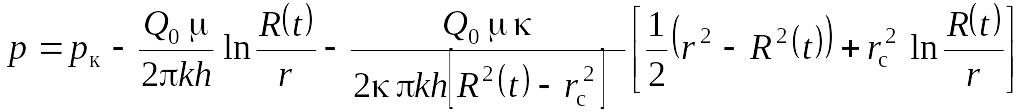
або

(9.170)

Для визначення радіусу знаходимо похідну і підставляємо в рівняння (9.164), враховуючи вираз для , тобто

(9.171)

Тут нехтували членами з і через їх малу величину.

Тоді розподіл тиску в пласті

(9.172)

і депресія тиску, коли ,

(9.173)

Відносна похибка в обчисленні депресії тиску порівняно з точним розв’язком не перевищує 5%.

Третя група представлена формальним методом Е.Б. Чекалюка. Для отримання розв’язку Е.Б.Чекалюк використав рівняння для визначення припливу рідини за заданої функції вибійного тиску і для визначення вибійного тиску за заданої функції відбору (див. § 9.5). Функції він подав у вигляді зображень Лапласа , причому

(9.174)

де символи позначають оригінал і зображення за Лапласом даної функції часу.

Згідно з відомою в області операційного числення теоремою Борела зображення інтегралів Дюамеля (див. § 9.5) відповідає добутку зображень підінтегральних функцій, тобто

(9.175)

(9.176)

Якщо ці зображення описують один і той же процес припливу, то , , і тоді із останніх виразів отримуємо таку рівність:

(9.177)

Застосувавши обернене перетворення цього виразу, маємо

(9.178)

або

(9.179)

Використовуючи ці зв’язки функцій припливу і депресії тиску, Е.Б. Чекалюк отримав ряд нових невідомих розв’язків задач пружного режиму.

У результаті Е.Б. Чекалюк показав, що у випадку заданої постійної депресії тиску розв’язки для прямолінійно-паралельного (одновимірного) і сферично-радіального (тривимірного) потоків зводяться до виразу (див. вище):

. (9.180)

Тоді і для плоско-радіального (двовимірного) потоку можна припускати такий самий розв’язок. Звідси дебіт свердловини, пущеної в роботу з постійною депресією тиску, Е.Б. Чекалюк пропонує визначати за формулою Дюпюї, прийнявши радіус збуреної зони за формулою (9.180). Числовий аналіз показав, що цей розв’язок точно співпадає зі складним розв’язком М. Маскета, вираженим функціями Бесселя першого і другого роду нульового порядку.

Оскільки за постійного відбору маємо точний розв’язок

, (9.181)

то за змінних дебіту і депресії тиску Е.Б. Чекалюк пропонує прийняти

, (9.182)

де 2,66 одержано як усереднену значину, .

Контрольні питання

1. Виведіть основне диференціальне рівняння пружного режиму фільтрації.

2. Запишіть і поясніть основну формулу пружного режиму фільтрації. В яких практичних випадках її застосовують і з якими обмеженнями?

3. Як визначити відстань від свердловини до тектонічного порушення за даними зміни вибійного тиску у часі?

4. Коли застосовують метод Хорнера, а коли – метод дотичної?

5. Що таке скін-ефект і як його визначають?