8.2 Прямолінійно-паралельна фільтрація ідеального газу за законом Дарсі

Використовуючи рівняння (3.38) стану ідеального газу Бойля-Маріотта

знайдемо функцію Лейбензона (3.55):

. (8.10)

Згідно з рівнянням (8.9) запишемо об’ємну витрату газу, зведену до атмосферного тиску р₀ і до тиску р відповідно:

; . (8.11)

Далі на основі встановленої аналогії запишемо відповідні фільтраційні параметри потоку ідеального газу.

Розподіл тиску вздовж пласта в разі фільтрації нестисливої рідини до галереї, що знаходиться на відстані L від початку координат, описується формулою:

, (8.12)

а для газу маємо розподіл функції Лейбензона за аналогічною формулою:

(8.13)

(8.14)

звідки розподіл тиску газу отримуємо у вигляді:

, (8.15)

тобто тиск газу вздовж пласта змінюється за параболічним законом.

Градієнт функції Лейбензона із рівняння (8.13)

(8.16)

(8.17)

звідки градієнт тиску

. (8.18)

Оскільки в рівнянні (8.18) тиск р є функцією координати х згідно з рівнянням (8.15), то градієнт тиску зростає з наближенням до галереї.

Масова швидкість фільтрації газу згідно з рівнянням (8.5) за

(8.19)

або після переходу до тиску з використанням виразу (8.10)

, (8.20)

звідки об’ємна швидкість фільтрації газу

. (8.21)

Зміна об’ємної швидкості фільтрації аналогічна зміні градієнта тиску.

Масова витрата ідеального газу за аналогією:

(8.22)

або після переходу до тиску з використанням виразу (8.10)

. (8.23)

Об’ємні витрати газу, зведені до атмосферного тиску р₀ і біжучого тиску в пласті р, відповідно будуть:

; (8.24)

. (8.25)

Масова витрата газу Q_м є постійною вздовж пласта, а об’ємна витрата Q зростає з наближенням до галереї (фізично це пояснюється розширенням газу через зменшення тиску).

Середній тиск газу в пласті

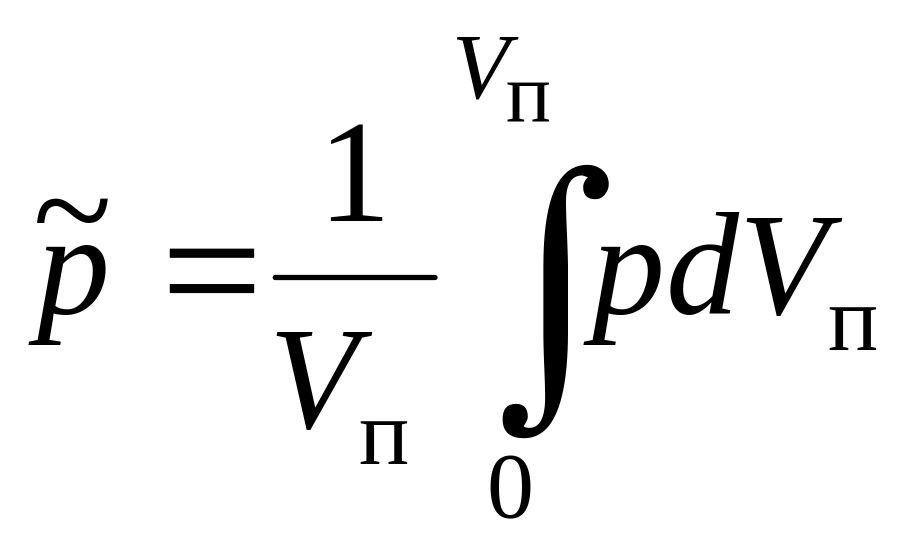. (8.26)

Оскільки об’єм пор пласта , , то

(8.27)

а після інтегрування отримуємо формулу середнього тиску ідеального газу в пласті:

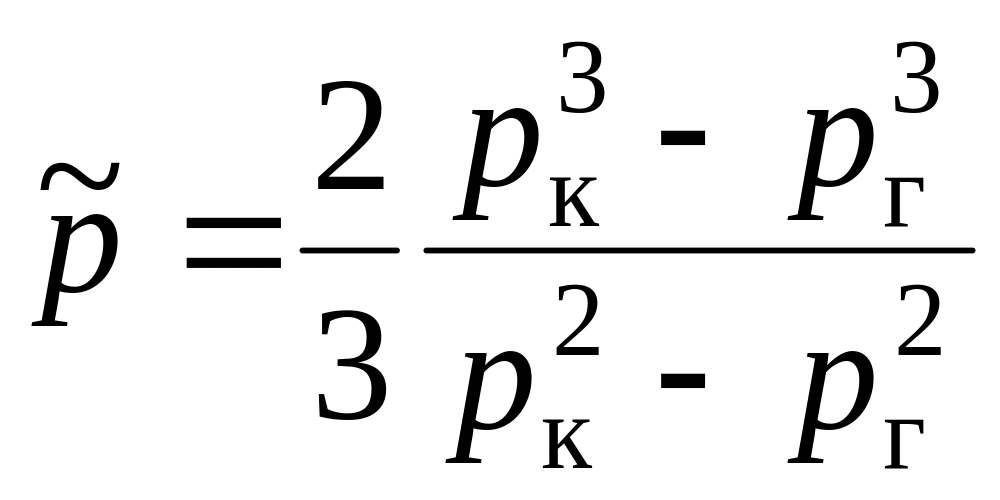. (8.28)

Для тиску маємо, що середній тиск .

8.3 Плоско-радіальна фільтрація ідеального газу за законом Дарсі

Розглянемо фільтрацію до свердловини, концентрично розміщеної в круговому пласті.

Розподіл функції Лейбензона за аналогією описується формулою:

, (8.29)

а розподіл тиску газу з використанням виразу (8.10) звідси отримуємо у вигляді:

. (8.30)

У даному випадку лійка депресії тиску значно крутіша, ніж у разі фільтрації нестисливої рідини (рис. 8.1).

Градієнт функції Лейбензона із формули (8.29)

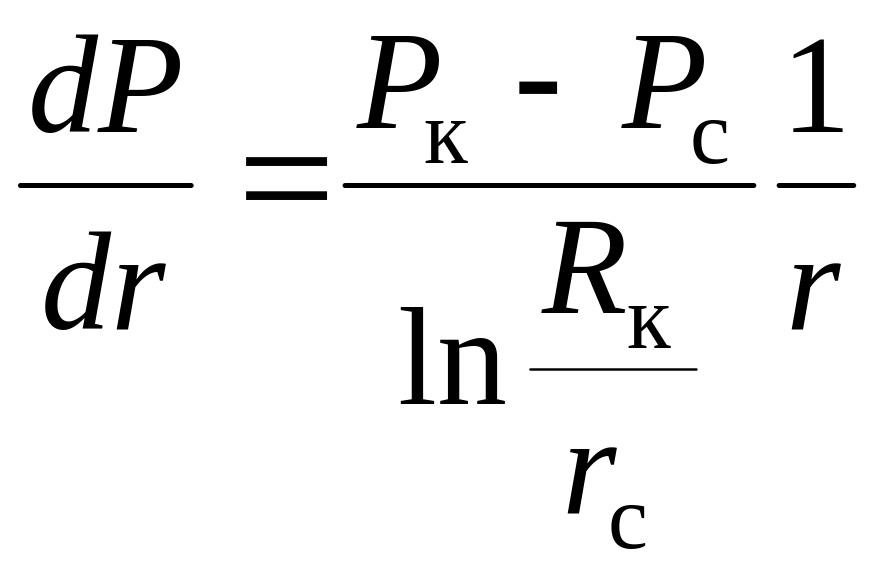(8.31)

або, аналогічно переходячи до тиску,

, (8.32)

звідки градієнт тиску

. (8.33)

Об’ємна швидкість фільтрації за тиску р в будь-якій точці пласта

. (8.34)

Дебіт газової свердловини в разі припливу ідеального газу за законом Дарсі за аналогією описуємо формулою:

, (8.35)

звідки отримуємо

. (8.36)

Об’ємну витрату газу необхідно також звести до атмосферної (нормальної 273,15 К чи стандартної 293,15 К) температури, використовуючи закон Шарля

або , (8.37)

тобто витрату Q₀ слід помножити на температурну поправку

, (8.38)

де – об’ємна витрата газу за атмосферних (стандартних чи нормальних) умов, оскільки – об’ємна витрата газу за умов атмосферного тиску і плас­тової температури; , Т_пл – температури відповідно атмосферна і пластова.

Індикаторна діаграма в разі фільтрації газу будується в координатах . У даному випадку вона представлена прямою лінією.