Контрольные вопросы

1. Каково назначение регрессионного анализа?

2. Что такое уравнение регрессии? Какова технология построения регрессионной модели?

3. Какие виды регрессии различают? Приведите примеры.

4. Что показывает коэффициент множественной корреляции Пирсона?

5. В чем заключается задача построения регрессионной зависимости?

6. Для чего применяется F-критерий Фишера? Как он вычисляется?

7. Какими параметрами определяется значимость коэффициента Пирсона?

8. Как построить линейную регрессионную модель в Excel? Что характеризует t-статистика?

Практическое задание № 5 ИспользованиЕ инструмента «корреляция»

Цель: закрепить знания о понятиях «корреляция», «коэффициент корреляции»; научиться применять инструмент «Корреляция».

Теоретические сведения

Корреляционный анализ – метод, позволяющий обнаружить зависимость между несколькими случайными величинами и количественно определить тесноту связи между ними.

Корреля́ция (корреляционная зависимость) — статистическая взаимосвязь двух или нескольких случайных величин (либо величин, которые можно с некоторой допустимой степенью точности считать таковыми). При этом изменения значений одной или нескольких из этих величин сопутствуют систематическому изменению значений другой или других величин.

При изучении корреляций стараются установить, существует ли какая-то связь между случайными величинами (например, между стажем рабочих и их производительностью труда). Если эта связь существует, то возможны следующие варианты зависимости между этими величинами:

1) увеличение одного показателя сопровождается возрастанием другого показателя (положительная корреляция);

2) увеличение одного показателя сопровождается уменьшением другого показателя (отрицательная корреляция).

Взаимосвязь между случайными величинами необходимо охарактеризовать количественно. Для этого в статистике введено понятие «коэффициент корреляции».

Коэффициент корреляции – показатель, который количественно выражает тесноту связи между случайными величинами.

Значение коэффициента корреляции могут варьировать в пределах от +1 до -1. В случае полной положительной корреляции этот коэффициент равен +1, а при полной отрицательной -1. В случаи, если коэффициент корреляции равен 0, обе переменные полностью независимы друг от друга.

В гуманитарных науках корреляция считается сильной, если ее коэффициент выше 0,60; если же он превышает 0,90, то корреляция считается очень сильной.

Взаимосвязь может быть полная (т. е. функциональная) и неполная (корелляционная), когда зависимость связанных величин искажена влиянием посторонних, дополнительных факторов. Примером функциональной связи является соотношение выпуска и потребления продукции, когда она дефицитна: во сколько раз больше выпуск, во столько раз больше продажа (все распродается, ничего не остается в запасе). Примером корреляционной связи может служить соотношение стажа рабочих и их производительности труда. Известно, что в среднем производительность труда рабочих тем выше, чем больше их стаж. Однако бывает, и нередко, что молодой рабочий (из-за влияния таких дополнительных факторов, как образование, здоровье и т. д.) работает лучше пожилого. Чем больше влияние этих дополнительных факторов, тем менее тесна связь между стажем и выработкой, и наоборот. В таком случае коэффициент корреляции между двумя величинами — стажем и производительностью — занимает промежуточное положение между нулем и единицей, в зависимости от силы (тесноты) взаимосвязи.

Корелляционный анализ рассматривает корреляционные связи не только между двумя переменными (парная корреляция), но и между многими (множественная корреляция).

В статистике существует несколько видов коэффициентов корелляции (коэффициент корелляции Кендалла, коэффициент корелляции Фехнера, коэффициент корелляции Пирсона, коэффициента ассоциации и т.д.). При анализе хозяйственной деятельности чаще используется коэффициент корреляции Пирсона.

Наиболее важным для практического использования является случай, когда связь между признаками X и Y линейная:

где и — коэффициенты уравнения регрессии.

Мера силы линейной связи признаков X и Y называется коэффициентом корреляции (коэффициент корреляции Пирсона). Коэффициенты корреляции, представляя количественную характеристику тесноты связи между признаками, дают возможность определить “полезность” факторных признаков при построении уравнений множественной регрессии. Величина коэффициентов корреляции служит также оценкой соответствия уравнению регрессии выявленным причинно-следственным связям.

Для применения корреляционного анализа необходимо, чтобы все рассматриваемые переменные были случайными и имели нормальный закон распределения. Причем выполнение этих условий необходимо только при вероятностной оценке выявленной тесноты связи.

Рассмотрим простейшие случай выявления тесноты связи — двумерную модель корреляционного анализа.

Для характеристики тесноты связи между двумя переменными обычно пользуются парным коэффициентом корреляции , если рассматривать генеральную совокупность, или его оценкой — выборочным парным коэффициентом , если изучается выборочная совокупность. Парный коэффициент корреляции в случае линейной формы связи вычисляют по формуле:

,

а его выборочное значение — по формуле: .

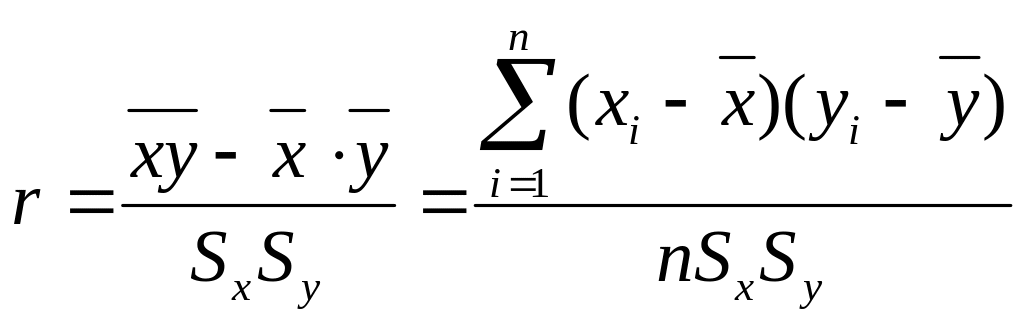При малом числе наблюдений выборочный коэффициент корреляции удобно вычислять по следующей формуле:

.

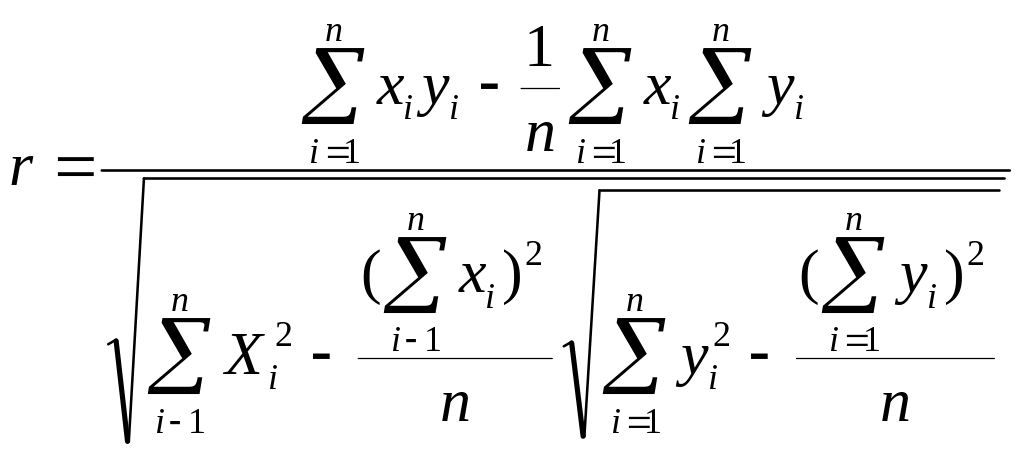Величина коэффициента корреляции изменяется в интервале .

При между двумя переменными существует функциональная связь, при — прямая функциональная связь. Если , то значение x и y в выборке некоррелированы; в случае, если система случайных величин имеет двумерное нормальное распределение, то величины x и y будут и независимыми.

Если коэффициент корреляции находится в интервале , то между величинами x и y существует обратная корреляционная связь. Это находит подтверждение и при визуальном анализе исходной информации. В этом случае отклонение величины y от среднего значения взяты с обратным знаком.

Если каждая пара значений величин x и y чаще всего одновременно оказывается выше (ниже) соответствующих средних значений, то между величинами существует прямая корреляционная связь и коэффициент корреляции находится в интервале .

Если же отклонения величины x от среднего значения одинаково часто вызывают отклонения величины y вниз от среднего значения и при этом отклонения оказываются все время различными, то можно предполагать, что значение коэффициента корреляции стремится к нулю.

Следует отметить, что значение коэффициента корреляции не зависит от единиц измерения и выбора начала отсчета. Это означает, что если переменные x и y уменьшить (увеличить) в К раз либо на одно и то же число С, то коэффициент корреляции не изменится.

Упражнение 1

На рис. 18 представлены исходные данные по срокам работы (в годах) и затратам на техническое обслуживание (в тысячах долларов в год) для пяти одинаковых печатных прессов. На основании этих данных вычислить корреляцию между сроком работы и затратами на техническое обслуживание.

Последовательность действий:

1. Открыть файл Анализ-ФинА-Иванов.xlsх. Добавить новый лист. Переименовать его, дав имя Корреляция. Разместить на листе Корреляция данные рис. 18.

2. С помощью команды Данные→ Анализ→ Анализ данных вызвать диалоговое окно Анализ данных. Выбрать инструмент анализа Корреляция (рис. 19).

Р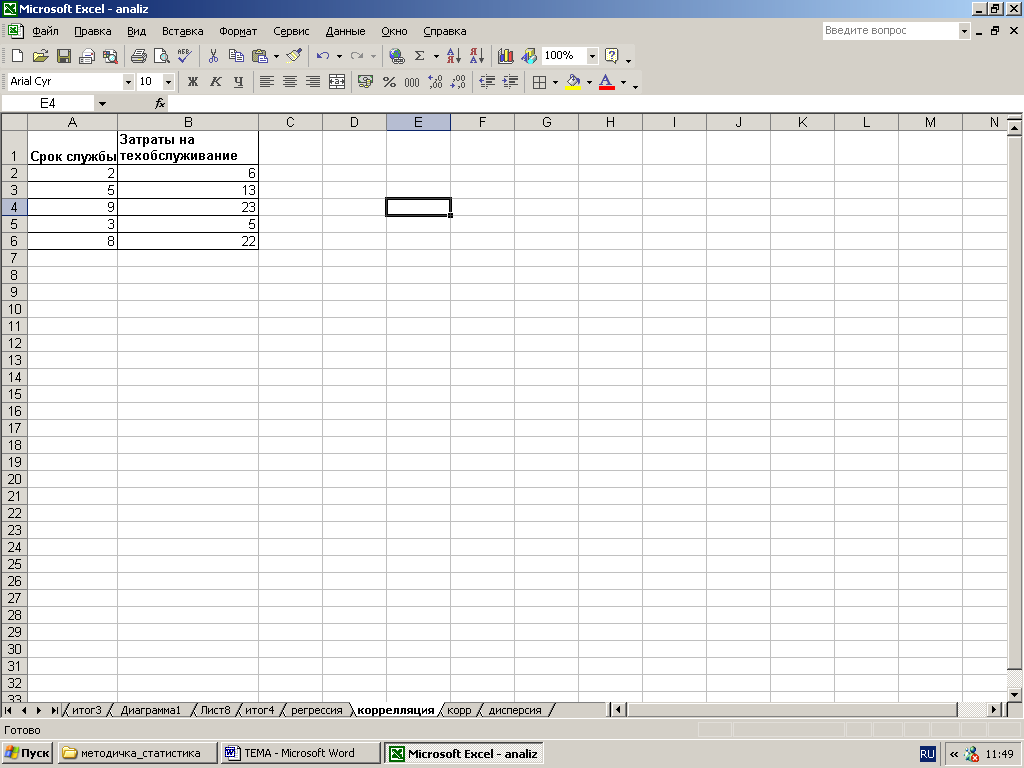 ис. 18.

3. В этом диалоговом окне задаются следующие параметры:

• в поле Входной интервал вводится ссылка на диапазон ячеек, содержащий анализируемые данные;

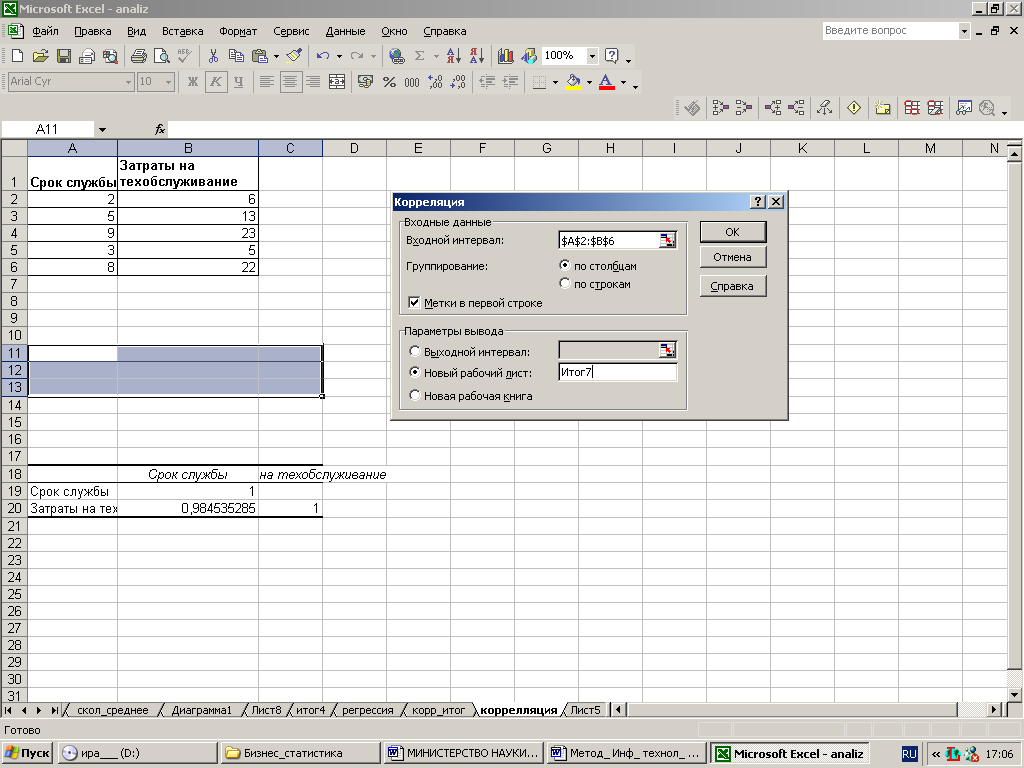
Рис. 19. Окно инструмента Корреляция.

• переключатель Группирование устанавливается в требуемое положение: По строкам или По столбцам, в зависимости от расположения исходных данных во входном диапазоне;

• флажок опции Метки в первой строке устанавливается в том случае, если первая строка во входном диапазоне содержит заголовок;

• переключатель в группе Параметры вывода может быть установлен в одно из трех положений: Выходной интервал, Новый рабочий лист или Новая рабочая книга;

• переключатель в группе Параметры вывода установить в положение Новый рабочий лист, дав ему имя Итог 8.

4. Нажмите на кнопку ОК.

Результаты расчетов представлены на рис. 20.

Коэффициент корреляции для этих данных равен 0,98. В данном случае коэффициент практически равен 1, что показывает сильную, почти линейную прямую зависимость между сроком работы пресса и затратами на его техническое обслуживание. Следовательно, можно сделать обоснованный вывод, что чем больше срок эксплуатации печатного станка, тем больше приходиться тратить средств на его ремонт и техническое обслуживание.

Р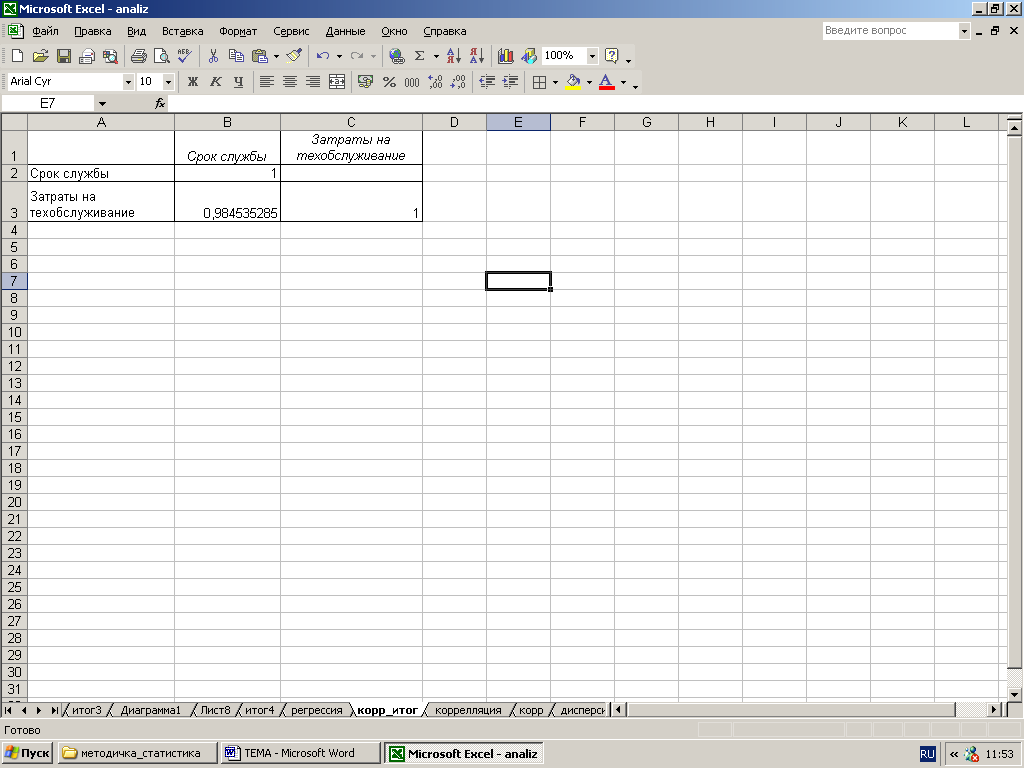 ис. 20

Индивидуальные задания

Задача № 5. (Приложение Б).

Задача № 5. (Приложение В).