Практическое задание № 2
ПРИМЕНЕНИЕ ИНСТРУМЕНТА «ОДНОФАКТОРНЫЙ ДИСПЕРСИОННЫЙ АНАЛИЗ»
Цель: закрепить знания о некоторых понятиях математической статистики, а именно: групповая дисперсия, внутригрупповая дисперсия, межгрупповая дисперсия и общая дисперсия; изучить и научиться применять процедуру расчетов (проверку гипотезы) с помощью однофакторного дисперсионного анализа.
Упражнение 1
Фирма продает свои товары в различных регионах Украины, имеет данные об объемах продаж в этих регионах по отдельным торговым точкам фирмы (рис. 4). Менеджеры фирмы хотят внести изменения в организацию регионального менеджмента, но перед этим они хотят установить, имеются ли различия в средних объемах продаж по данным регионам и являются ли они случайными или неслучайными, существенными или несущественными. |
При использовании пакета Анализ данных необходимо сгруппировать данные определенным образом. Например, данные для каждого из пяти регионов представить в отдельном столбце, в первой строке которого содержится название региона.
Последовательность действий:
Открыть файл Анализ-ФинА-Иванов.xlsx. Добавить новый лист и дать ему имя Дисперсия_1. Разместить на листе Дисперсия_1 данные рис. 4.
Р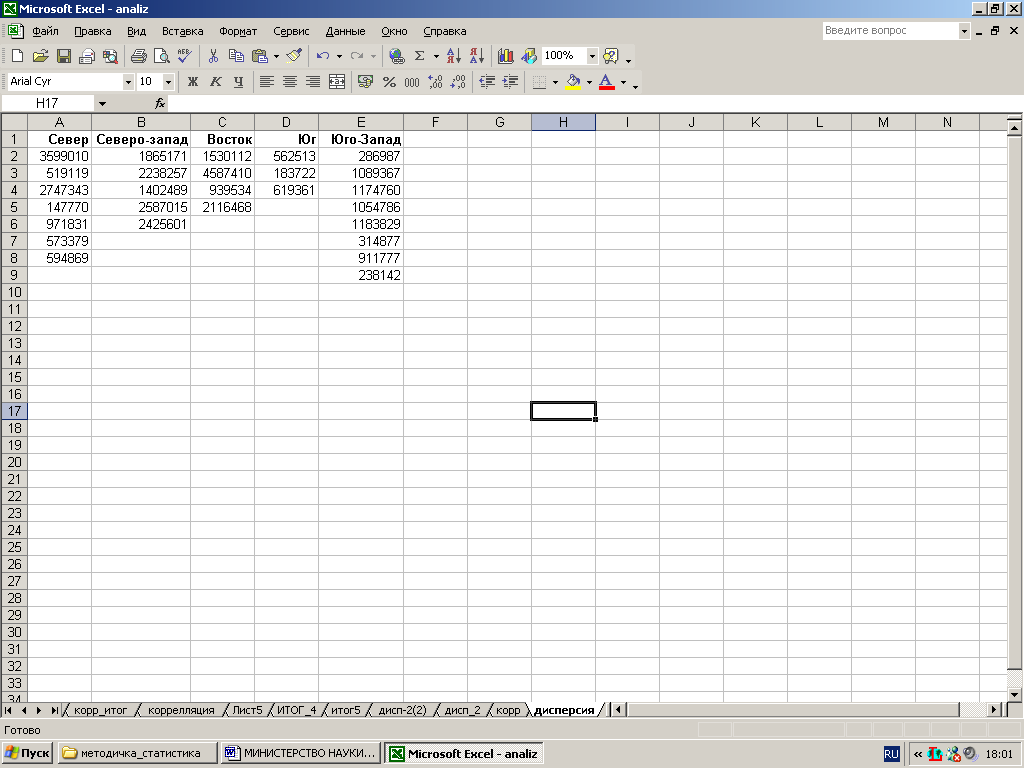
ис.
4. Объемы продаж
продукции фирмы
по регионам Украины,
грн.
Вызвать диалоговое окно Анализ данных, выполнив команду Данные→ Анализ→ Анализ данных. Выбрать инструмент анализа Однофакторный дисперсионный анализ.
3. В открывшемся диалоговом окне Однофакторный дисперсионный анализ (рис. 5) ввести информацию для проведения анализа, а именно, установить следующие параметры:
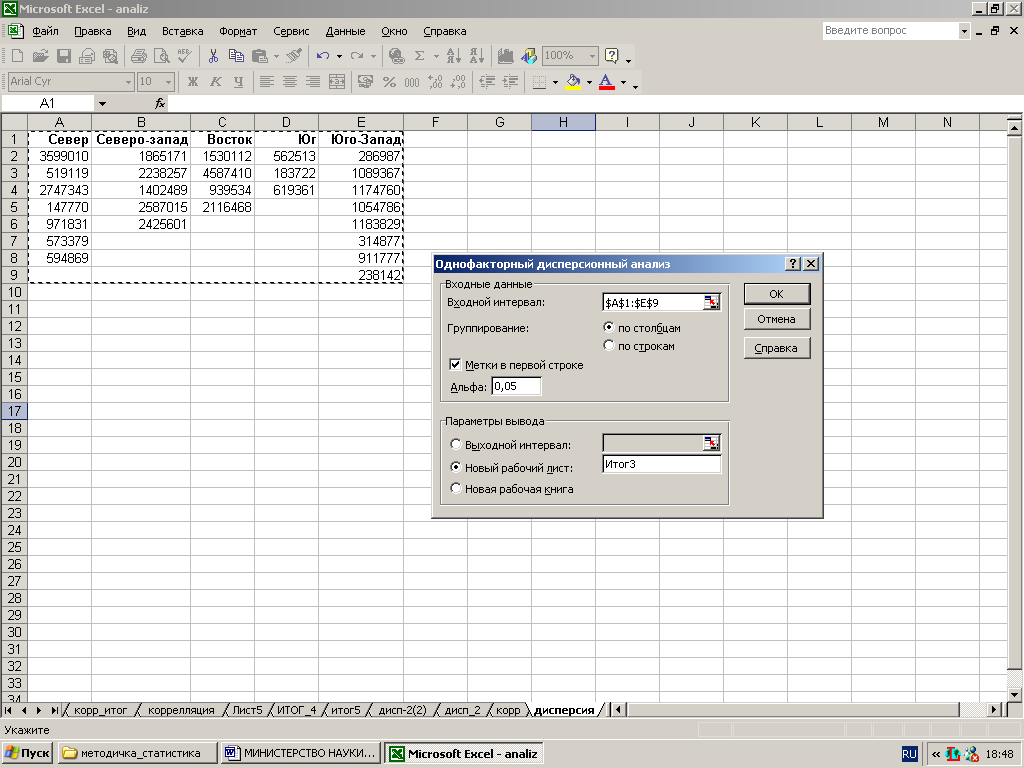
Рис. 5. Диалоговое окно инструмента Однофакторный дисперсионный анализ
щелкнуть в поле Входной интервал и ввести диапазон ячеек А1:Е9;
установить переключатель по столбцам в группе Группирование;
установить флажок Метки в первой строке;
оставить в поле Альфа значение 0,05 (установленное по умолчанию) или изменить его на другое значение в диапазоне от 0 до 1;
определить параметры вывода — Новый рабочий лист, дав ему имя Итог 3.
Результаты расчета отображены на рис. 6.
Р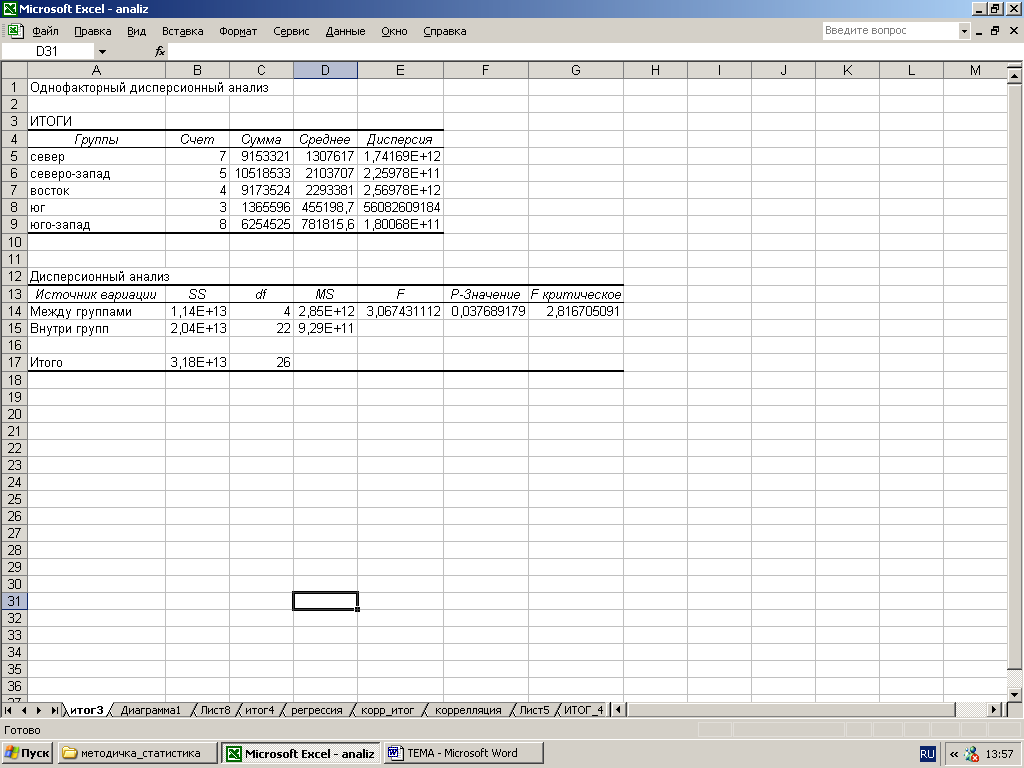
ис.
6. Результаты расчета
Первая часть результатов (таблица «Итоги») представляет собой отчет описательной статистики для каждого региона: количество наблюдений (счет), сумма, среднее и дисперсия объема продаж в данном регионе (см. практическое задание 1).
Для понимания второй части таблицы необходимо знать следуюшие понятия математической статистики: групповая дисперсия, внутригрупповая дисперсия, межгрупповая дисперсия и общая дисперсия.
Групповая дисперсия характеризует вариацию значений каждой группы относительно ее среднего значения.
Внутригрупповой дисперсией называют среднеарифметическую групповых дисперсий, взвешенную на объем групп (частоту значений).
Межгрупповая дисперсия – это дисперсия групповых средних относительно среднего значения всей совокупности.
Общая дисперсия характеризует вариацию, вызванную действием всех уровней фактора. Она вычисляется по индивидуальным значениям всей совокупности относительно ее среднего значения. Общая дисперсия равна сумме внутригрупповой и межгрупповой дисперсий.
Вторая часть (таблица «Дисперсионный анализ») содержит выведенную информацию, т.е. данные, относящиеся к вопросу о значимости наблюдаемых результатов продаж в разрезе межгрупповых и внутригрупповых показателей. В ней представлены:
Df — число степеней свободы (независимые значения);
SS — сумма квадратов отклонений;
MS — дисперсия, рассчитывается как отношение SS/Df;
F — отношение дисперсии регрессии к дисперсии остатка.
Дисперсионный анализ позволяет оценить вероятность появления расхождения между фактическими и предполагаемыми значениями при условии, что наблюдаемые различия вызваны случайными событиями. В нашем случае уровень вероятности (Р-Значение) равно 0,0377. На основании этого можно сделать вывод, что различия в объемах продаж, скорее всего, носят неслучайный характер и вызваны конкретными обстоятельствами (вероятность составляет 96%), а вероятность случайных обстоятельств равна всего 4%.
Расчетное значение критерия Фишера (F) равно 3,067. Сравнивая это значение с табличным значением (F критическое) – 2,817, мы видим, что расчетное значение больше табличного, т.е. можно сделать вывод о том, что региональный фактор влияет на объем продаж.
Значит, при изменении маркетинговой политики фирмы необходимо учитывать региональный фактор, и стоит более детально изучить различия в демографических и экономических условиях регионов и степень их влияния на объем продаж.
Подводя итоги, можно сказать, что целью дисперсионного анализа является проверка статистической значимости различия между средними (для групп или переменных). Эта проверка проводится с помощью разбиения суммы квадратов на компоненты, т.е. с помощью разбиения общей дисперсии (вариации) на части, одна из которых обусловлена случайной ошибкой (то есть внутригрупповой изменчивостью), а вторая связана с различием средних значений. Последняя компонента дисперсии затем используется для анализа статистической значимости различия между средними значениями. Если это различие значимо, нулевая гипотеза отвергается и принимается альтернативная гипотеза о существовании различия между средними.
Индивидуальные задания
Задача № 2. (Приложение Б).
Задача № 2. (Приложение В).