
- •Тема 1. Описательная статистика
- •1.1. Общие сведения
- •1.2. Cтатистические функции ms Excel для вычисления основных характеристик случайной величины
- •Практическое задание № 1
- •Контрольные вопросы
- •Тема 2. Дисперсионный анализ
- •Практическое задание № 2
- •Контрольные вопросы
- •Практическое задание № 3
- •Теоретические сведения
- •Контрольные вопросы
- •Тема 3. Корреляционно – регрессионый анализ
- •Практическое задание № 4
- •Теоретические сведения
- •Контрольные вопросы
- •Практическое задание № 5 ИспользованиЕ инструмента «корреляция»
- •Теоретические сведения
- •Контрольные вопросы
- •Практическое задание № 6 использование функции линейн
- •Теоретические сведения
- •Контрольные вопросы
- •Тема 5. Прогнозирование и бизнес-анализ средстами ms excel
- •5.1. Прогнозирование на основе анализа временных рядов
- •Факторы, влияющие на значения временного ряда
- •5.1.Средства ms Excel для анализа временных рядов
- •5.3. Применение трендового анализа
- •Практическое задание № 7
- •Теоретические сведения
- •Контрольные вопросы
- •5.4. Прогнозирование методом скользящего среднего
- •Практическое задание № 8
- •Теоретические сведения
- •Контрольные вопросы
- •Практическое задание № 9
- •Теоретические сведения
- •Контрольные вопросы
- •Практическое задание № 11
- •Теоретические сведения
- •Контрольные вопросы
- •Практическое задание № 12
- •Теоретические сведения
- •4. Строится модель прогнозирования: ,
- •Контрольные вопросы
- •Контрольные вопросы по вычислительной практике
- •Индивидуальные задания
- •Индивидуальные задания
Контрольные вопросы
В чем состоит основная идея применения метода сглаживания?
Какой вид имеет базовое уравнение метода сглаживания?
В чем отличие метода сглаживания от методов, основанных на регрессии?
В чем суть средства экспоненциальное сглаживание? Как его вызвать?
Что такое автокорреляция?
Какой функцией можно воспользоваться для проведения проверки автокорреляции?
Практическое задание № 12
АНАЛИЗ МОДЕЛИ С АДДИТИВНОЙ И МУЛЬТИПЛИКАТИВНОЙ КОМПОНЕНТОЙ
Цель: ознакомиться и научиться анализировать прогнозные модели с аддитивной и мультипликативной компонентой.
Теоретические сведения
Моделью с аддитивной компонентой называется такая модель, в которой вариация значений переменной во времени наилучшим образом описывается путем сложения отдельных компонент.
В моделях как с аддитивной, так и с мультипликативной компонентой общая процедура анализа примерно одинакова.
Алгоритм построения прогнозной модели
Для прогнозирования объема продаж, имеющего сезонный характер, предлагается следующий алгоритм построения прогнозной модели:
1. Определяется тренд, наилучшим образом аппроксимирующий фактические данные. Существенным моментом при этом является предложение использовать полиномиальный тренд, что позволяет сократить ошибку прогнозной модели.
2. Вычитая из фактических значений объемов продаж значения тренда, определяют величины сезонной компоненты и корректируют их таким образом, чтобы их сумма была равна нулю. Этот процесс называется десезонализацией данных. Расчет тренда на основе получeнных десезонализированных данных.
3. Рассчитываются ошибки модели как разности между фактическими значениями и значениями модели.
4. Строится модель прогнозирования: ,
где F — прогнозируемое значение; Т — тренд; S — сезонная компонента; Е — ошибка модели.
Расчет среднего отклонения или среднеквадратической ошибки для обоснования соответствия модели исходным данным или для выбора из множества моделей наилучшей.
5. На основе модели строится окончательный прогноз объема продаж. Для этого предлагается использовать методы экспоненциального сглаживания, что позволяет учесть возможное будущее изменение экономических тенденций, на основе которых построена трендовая модель. Сущность данной поправки заключается в том, что она нивелирует недостаток адаптивных моделей, а именно позволяет быстро учесть наметившиеся новые экономические тенденции:
![]() ,
где Fпр
t
— прогнозное значение объема продаж;
Fф
t–1
— фактическое значение объема продаж
в предыдущем году; Fмt
— значение модели; а
— константа сглаживания.
,
где Fпр
t
— прогнозное значение объема продаж;
Fф
t–1
— фактическое значение объема продаж
в предыдущем году; Fмt
— значение модели; а
— константа сглаживания.
Практическая реализация данного метода выявила следующие его особенности:
для составления прогноза необходимо точно знать величину сезона. Исследования показывают, что множество продуктов имеют сезонный характер; величина сезона при этом может быть различной и колебаться от одной недели до десяти лет и более;
применение полиномиального тренда вместо линейного позволяет значительно сократить ошибку модели;
при наличии достаточного количества данных метод дает хорошую аппроксимацию и может быть эффективно использован при прогнозировании объема продаж в инвестиционном проектировании.
Представим один из возможных алгоритмов построения прогноза объема реализации для продуктов с сезонным характером продаж. Сразу следует отметить, что перечень таких товаров гораздо шире, чем это кажется. Дело в том, что понятие «сезон» в прогнозировании применимо к любым систематическим колебаниям — например, если речь идет об изучении товарооборота в течение недели под термином «сезон» понимается один день. Кроме того, цикл колебаний может существенно отличаться (как в большую, так и в меньшую сторону) от величины в один год. И если удается выявить величину цикла этих колебаний, то такой временной ряд можно использовать для прогнозирования с использованием аддитивных и мультипликативных моделей.
Аддитивную
модель прогнозирования можно представить
в виде формулы:
![]() ,
,
где F — прогнозируемое значение; Т — тренд; S — сезонная компонента; Е — ошибка прогноза.
Применение мультипликативных моделей обусловлено тем, что в некоторых временных рядах значение сезонной компоненты представляет собой определенную долю трендового значения. Эти модели можно представить формулой:
![]() .
.
На практике отличить аддитивную модель от мультипликативной можно по величине сезонной вариации. Аддитивной модели присуща практически постоянная сезонная вариация, тогда как у мультипликативной она возрастает или убывает; графически это выражается в изменении амплитуды колебания сезонного фактора (рис. 53).
Р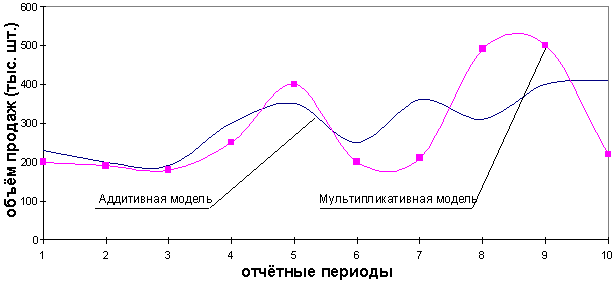 ис.
53. Аддитивная и мультипликативная модель
ис.
53. Аддитивная и мультипликативная модель
Если когда-либо Вам понадобится прогнозировать объемы продаж, то Вам наверняка нужно будет учитывать тенденции сезонности, так как данные о продажах и соответствующие им временные ряды зачастую носят именно сезонный характер. Например, объемы продаж могут достигать пика в начале года (рождественские и новогодние праздники), а затем, до начала следующего года, постепенно возвращаться к исходному, более низкому уровню.
Причиной такого положения дел может стать природа продукции: например, спрос на теплую верхнюю одежду весной и летом намного ниже, чем осенью и зимой. Сезонность объемов продаж может также объясняться особенностями финансового года: покупатели обычно увеличивают объемы закупок в тот период года, когда объем денежной массы максимален. В подобных случаях методы регрессии и простого сглаживания могут оказаться неприменимыми для прогнозирования тенденций сезонности.
Когда временной ряд отражает тенденции сезонности, изменение формулы сглаживания просто необходимо. При сезонном прогнозировании прогноз не просто составляется на основе предшествующих результатов наблюдений, он базируется на двух компонентах:
Компонент тренда представляет тенденцию в базовой линии либо к повышению, либо к понижению.
Компонент сезонности представляет любое резкое понижение, повышение или пик базовой линии, которые происходят с одинаковыми промежутками времени.
Процесс сезонного сглаживания проходит две фазы: фазу инициализации, во время которой определяются размеры тенденции и величина компонентов сезонности, и фазу прогнозирования. На основе этих компонентов разрабатываются перспективные оценки.
Упражнение 1
На рис. 54 представлены объёмы сбыта мороженого «Пломбир» за два сезона. Составить прогноз продаж продукции на следующий год по месяцам. |
Последовательность действий:
Открыть рабочую книгу Анализ-ФинА-Иванов.х1sх.
Добавить лист Сезон. В качестве исходных значений используем данные рис. 54.
Построить диаграмму, выделив диапазон ячеек С2:С25, щелкнуть на кнопке график группы диаграммы вкладки Вставка и из раскрывающегося списка выбрать вид диаграммы График с маркерами.
Р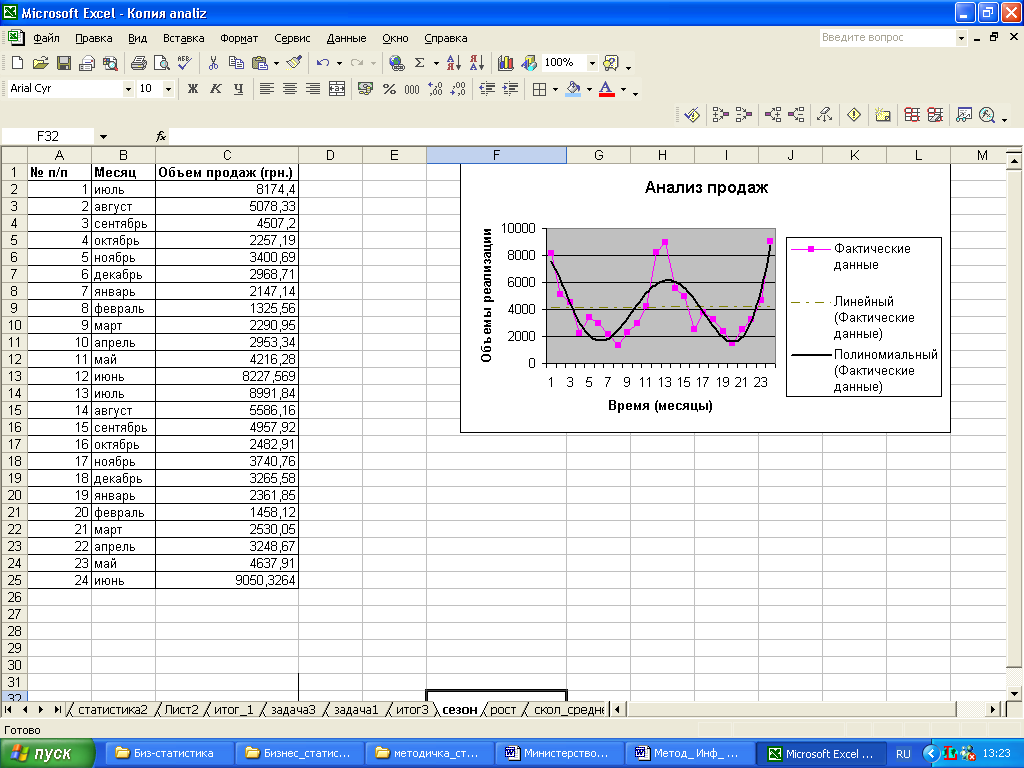 ис.
54. Объём сбыта мороженого «Пломбир» за
два сезона
ис.
54. Объём сбыта мороженого «Пломбир» за
два сезона
С помощью элементов управления, расположенных на вкладке Макет (Работа с диаграммами) задать название диаграммы и ее осей
Получится график, представленный на рис. 55.
Определить тренд, наилучшим образом аппроксимирующий фактические данные. (Для этого рекомендуется использовать полиномиальный тренд, что позволяет сократить ошибку прогнозной модели.).
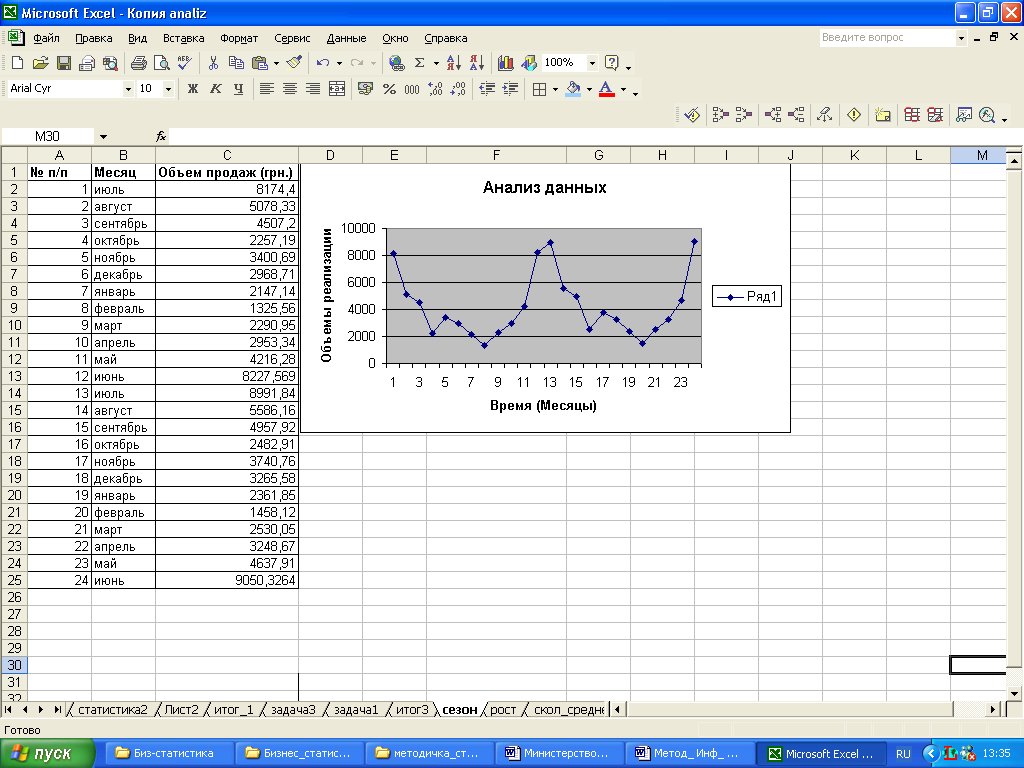
Рис.55. График объёма сбыта мороженого «Пломбир» за два сезона
Щелкнуть правой кнопкой мыши по графику и из контекстного меню выбрать команду Выбрать данные. В открывшемся диалоговом окне Выбор источника данных в списке Элементы легенды (ряды) выделить Ряд1, нажать на кнопку Изменить и задать имя ряда Фактические данные. Нажать на кнопку ОК.
Щелкнуть правой кнопкой мыши по одному из маркеров графика и из контекстного меню выбрать команду Добавить линию тренда. В открывшемся диалоговом окне Формат линии тренда на вкладке Параметры линии тренда установить кнопку опции Линейная и установить флажки опций Нажать на кнопку ОК..
Аналогично создать полиномиальный тренд, задав для него Степень, равную 5 и установив флажки показывать уравнение на диаграмме и поместить на диаграмму величину достоверности апроксимации (R^2).
В результате получаться диаграммы, представленные на рис. 56.
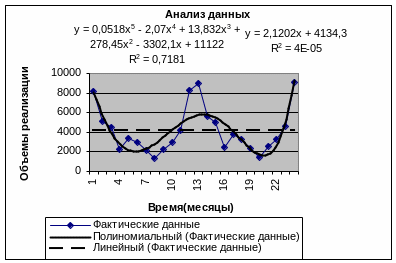
Рис. 56. Сравнительный анализ полиномиального и линейного тренда.
Из рис. 56 видно, что полиномиальный тренд аппроксимирует фактические данные гораздо лучше, чем предлагаемый обычно в литературе линейный. Коэффициент детерминации полиномиального тренда (0,7181) гораздо выше, чем линейного (4E-05). Применение других типов тренда (логарифмический, степенной, экспоненциальный, скользящее среднее) также не даёт такого эффективного результата. Они неудовлетворительно аппроксимируют фактические значения, коэффициенты их детерминации ничтожно малы:
логарифмический R2 = 0,0166;
степенной R2 = 0,0197;
экспоненциальный R2 = 8Е-05.
Выполнить расчет тренда (T) на основе полученного на диаграмме уравнения полинома и, вычитая из фактических значений объёмов продаж значения тренда, определить величины сезонной компоненты, используя при этом рис. 57.

Рис. 57. Расчёт значений сезонной компоненты.
Заполнить таблицу исходными данными, вычислить значения точек тренда по формуле, определенной на диаграмме, затем в ячейку Е2 ввести формулу C2-D2, затем с помощью инструмента Автозаполнение протянуть эту формулу до конца ячейки Е25 (см. Алгоритм расчета на рис. 57).
Скорректируем значения сезонной компоненты таким образом, чтобы их сумма была равна нулю.
Последовательность действий:
Открыть рабочую книгу Анализ-ФинА-Иванов.х1sх.
Добавить лист Сезон2. В качестве исходных значений использовать данные и алгоритм расчета, представленные на рис. 58. Полученная сезонная компонента (S) станет элементом построения модели прогнозирования: .
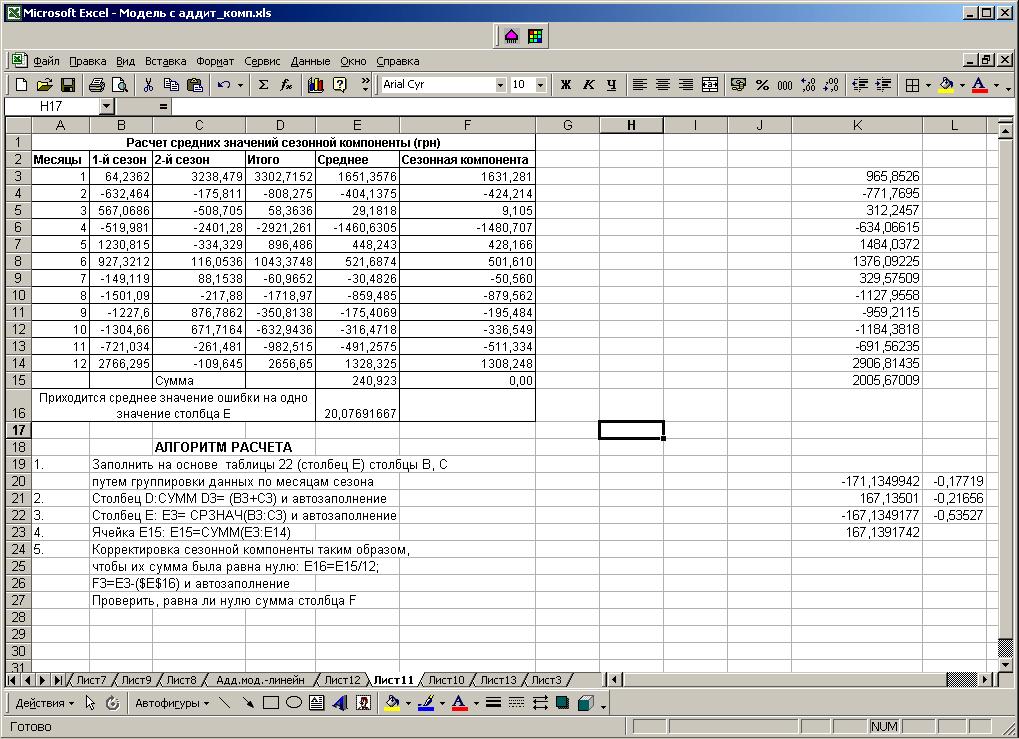
Рис. 58. Расчет средних значений сезонной компоненты.
Рассчитываем ошибки модели (Е) как разности между фактическими значениями и значениями модели.
Последовательность действий:
Открыть рабочую книгу Анализ-ФинА-Иванов.х1sх.
Добавить лист Сезон_ошибка. Расчеты выполнить, используя алгоритм расчета, представленный на рис. 59.
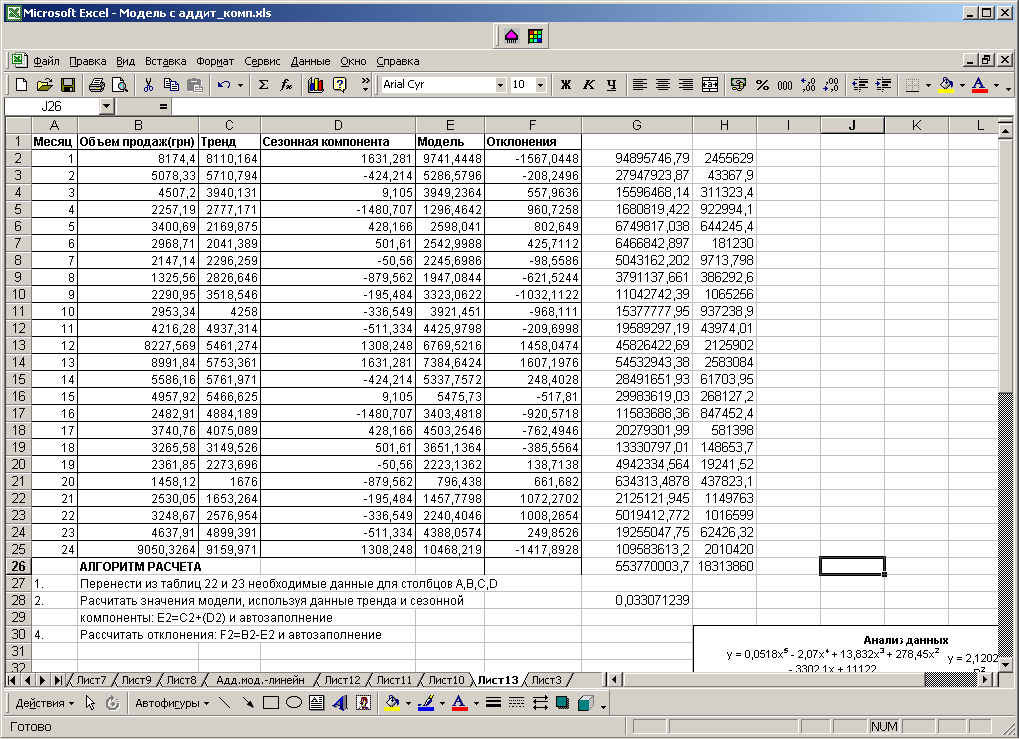
Рис. 59. Расчет ошибок
3.
Найти среднеквадратическую ошибку
модели (Е) по формуле:
![]() ,
где: Т
— трендовое значение объёма продаж; S
— сезонная компонента; О
— отклонения модели от фактических
значений.
,
где: Т
— трендовое значение объёма продаж; S
— сезонная компонента; О
— отклонения модели от фактических
значений.
Е= 0,03307 или 3,3 %
Величина полученной ошибки позволяет говорить, что построенная модель хорошо аппроксимирует фактические данные, т.е. она вполне отражает экономические тенденции, определяющие объём продаж, и является предпосылкой для построения прогнозов высокого качества.
Построим модель прогнозирования:
F = T + S ± E
Построенная модель представлена графически на рис. 60.
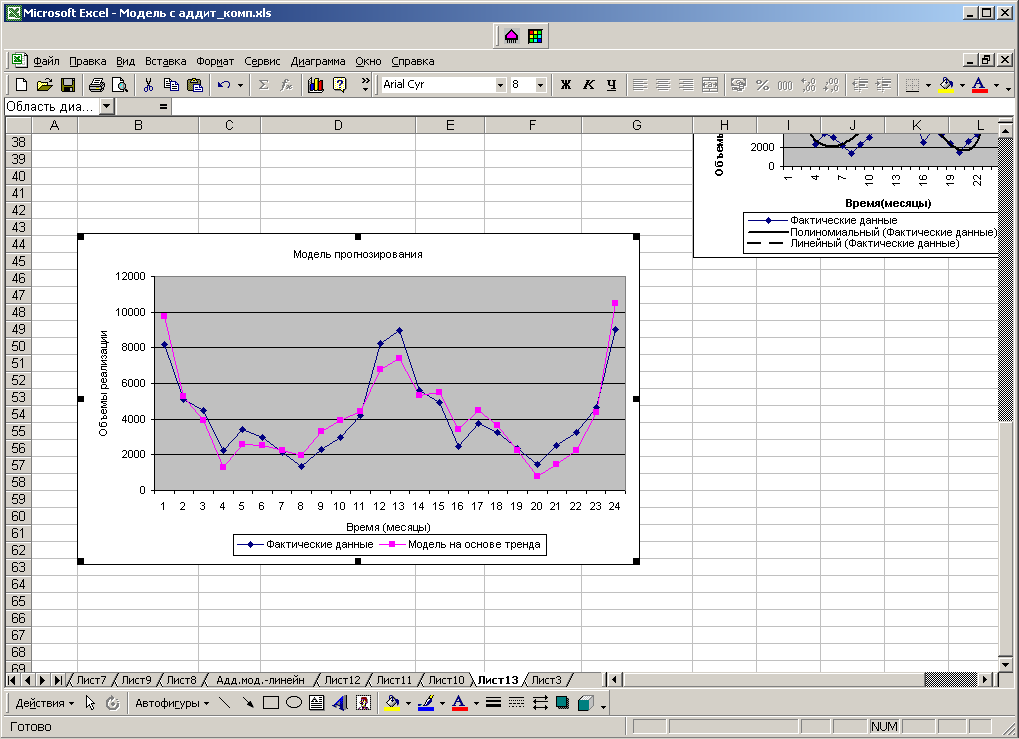
Рис. 60. Модель прогнозирования
15. На основе модели построить окончательный прогноз объёма продаж. Для смягчения влияния прошлых тенденций на достоверность прогнозной модели, предлагается сочетать трендовый анализ с экспоненциальным сглаживанием. Это позволит нивелировать недостаток адаптивных моделей, т.е. учесть наметившиеся новые экономические тенденции:
Fпр t = a Fф t-1 + (1-а) Fм t
где: Fпр t — прогнозное значение объёма продаж;
Fф t-1 — фактическое значение объёма продаж в предыдущем году;
Fм t — значение модели;
а — константа сглаживания.
Константу сглаживания рекомендуется определять методом экспертных оценок как вероятность сохранения существующей рыночной конъюнктуры, т.е. если основные характеристики изменяются и колеблются с той же скоростью и амплитудой что и прежде, значит предпосылок к изменению рыночной конъюнктуры нет, и, следовательно, а < 1, если наоборот, то а > 0.
Таким образом, прогноз на январь третьего сезона определяется следующим образом.
Определяем прогнозное значение модели:
Fм t = 2273,7 + (-50,56) = 2223 ± (2223*0,033)(грн.)
Фактическое значение объёма продаж в предыдущем году (Fф t-1) составило 2 361 грн. Принимаем коэффициент сглаживания 0.8. Получим прогнозное значение объёма продаж:
Fпр t = 0,8*2 361 + (1-0.8)*2223 = 2334 (грн.)
Для учёта новых экономических тенденций рекомендуется регулярно уточнять модель на основе мониторинга фактически полученных объёмов продаж, добавляя их или заменяя ими данные статистической базы, на основе которой строится модель.
Кроме того, для повышения надёжности прогноза рекомендуется строить все возможные сценарии прогноза и рассчитывать доверительный интервал прогноза.
Индивидуальные задания
Задача № 10. (Приложение Б).
Задача № 10. (Приложение В).
