2.2. Розрахунок параметрів циліндричної зубчастої передачі

З умови контактної міцності визначають міжосьову відстань передачі:

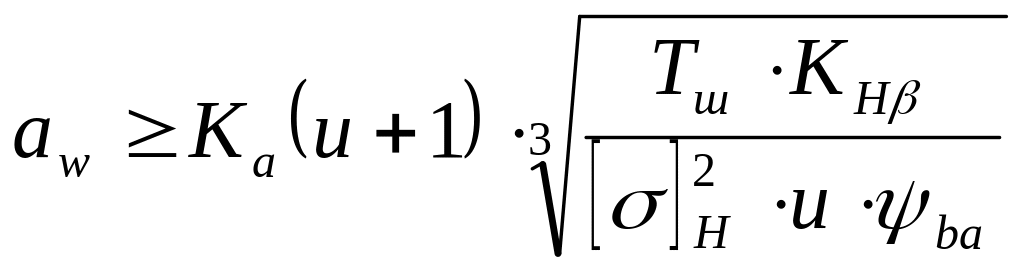, [мм]. (2.8)

При цьому у формулу (2.8) підставляють не передаточне число передачі u, а передаточне відношення і, оскільки число зубів z_ш і z_к невідомі і невідомо .

Тоді формула (2.8) має вигляд:

, [мм], (2.9)

де K_a – коефіцієнт, що враховує форму суміжних зубів, механічні властивості матеріалу, степінь перекриття, розподіл наванта­ження між ланками і динамічність навантаження. Для стальних прямозубих коліс ; для косозубих ;

Т_ш – крутний момент на валу шестірні, Н мм;

– допустиме контактне напруження для менш міцного з матеріалів пари зубчастих коліс, МПа;

К_Нβ – коефіцієнт, який враховує нерівномірність розподілу навантаження по довжині зуба (табл. 2.6). При постійному навантаженні ;

– коефіцієнт ширини вінця колеса, визначають за формулою:

, (2.10)

де – коефіцієнт ширини колеса по діаметру (табл. 2.6).

Для стандартних редукторів значення Ψ_ba округлюють до стандартного значення з ряду: 0,125; 0,150; 0,160; 0,250; 0,315; 0,400; 0,500; 0,630; 0,800; 1,00; 1,25. Переважно Ψ_ba приймають для прямозубих передач в межах 0,125…0,250; для косозубих – в межах 0,25…0,63.

Таблиця 2.6. Значення Ψ_ba, що рекомендується, і орієнтовне значення К_Нβ

Розміщення колеса відносно опор	Твердість поверхні зубів
	≤ НВ 350		> НВ 350
	Ψbd	Кнβ	Ψbd	Кнβ
Консольне	0,3…0,4	1,20…1,35	0,2…0,25	1,25…1,45
Симетричне	0,8…1,4	1,0…1,15	0,4…0,9	1,05…1,25
Несиметричне	0,6…1,2	1,10…1,25	0,3…0,6	1,16…1,35
Примітка. Великі значенія Ψbd приймають при постійних навантаженнях. Менше значення КHβ приймають для передач з коефіцієнтом Ψbd=0,4; більше – при консольному розташуванні коліс при збільшенні Ψbd до 0,6 і при несиметричному розташуванні коліс при збільшенні Ψbd до 0,8. При постійному навантаженні КHβ=1.

Отримане значення a_w округлюють до стандартного значення по СТ СЭВ 229-75 (мм). Для стандартної передачі:

ряд 1: 40; 50; 63; 80; 100; 125; 160; 200; 250; 315; 400; 500; 630; 800;

ряд 2: 71; 90; 112; 140; 180; 224; 280; 355; 450; 560; 710; 900.

Для нестандартної передачі a_w округлюють до цілого числа.

Вибирають модуль m з інтервалу (0,01…0,02)a_w по СТ СЭВ 310-76 (мм):

ряд 1: 1; 1,5; 2; 2,5; 3; 4; 5; 6; 8; 10; 12; 16; 20;

ряд 2: 1,25: 1,375; 1,75; 2,25; 2,75; 3,5; 4,5; 5,5; 7; 9; 11; 14.

Для косозубих коліс стандартний модуль – нормальний m_n.

Визначають сумарне число зубів :

– для прямозубих коліс:

; (2.11)

– для косозубих коліс:

, (2.12)

де β – кут нахилу зубів, приймають ;

m_t – торцевий модуль, мм.

Визначають число зубів шестерні z_ш і колеса z_к:

; . (2.13)

Округлюють z_ш і z_к до цілого числа.

Визначають передаточне число:

. (2.14)

Різниця з раніше прийнятим передаточним відношенням i повинно бути менше 2,5% при i ≤ 4,5 і 4% при i ≥ 4,5.

Уточнюють міжосьову відстань a_w за формулами:

– для прямозубих передач:

; (2.15)

– для косозубих передач:

. (2.16)

Якщо значення і не збігаються, приводять до першого значення . Для прямозубих передач – зміною числа зубів z_ш і z_к, для косозубих – зміною кута β, значення якого визначають із виразів:

;

. (2.17)

Якщо для косозубих передач у формулу (2.9) підставляють значення , необхідно перевірити виконання умови:

. (2.18)

При виконанні цієї умови в зачепленні знаходяться не менше двох пар зубів.

Після визначення a_w за формулою (2.9) можна задатися числом зубів z_ш з урахуванням умови , потім визначити z_к і модуль:

; ; . (2.19)

Значення модуля m_n округлюють до стандартного значення.

Визначають основні геометричні розміри шестірні і колеса:

– діаметри ділильних кіл:

для прямозубих коліс:

; ; (2.20)

для косозубих коліс:

; ; (2.21)

– діаметри вершин зубів:

для прямозубих коліс:

; ; (2.22)

для косозубих коліс:

; ; (2.23)

– ширину вінця колеса: ;

– ширину шестірні: ;

– коефіцієнт ширини колеса по діаметру: ;

– перевіряють, щоб уточнена міжосьова відстань була рівна раніше принятому a_w.

Визначають колову швидкість коліс:

, [м/с], (2.24)

де ω_ш кутова швидкістьшестерні, рад/с, d_ш, мм. За табл.2.7 призначають степінь точності коліс.

Розраховують сили, які діють в зачепленні: колова F_t, радіальна F_r і осьова F_a:

– для прямозубої передачі:

; (2.25)

; (2.26)

– для косозубої передачі:

; (2.27)

; (2.28)

, (2.29)

де α – кут зачеплення, в нормальних колесах ;

β – кут нахилу зубів.

Таблиця 2.7. Степінь точності коліс

Вид передачі	Вид зубів	Степінь точності
		6-а	7-а	8-а	9-а
		Гранична швидкість V, м/с
Циліндрична	прямі	15	10	6	3
	косі	30	15	10	6
Конічна	прямі	9	6	4	2,5
Примітка: 9-у степінь точності допускається застосовувати для тихохідних відкритих передач.

Визначають розрахункові контактні напруження i порівнюють з допустимими :

, (2.30)

де Z_H, Z_M , Z_ε – коефіцієнти, що враховують відповідно форму зубів, механічні властивості матеріалу коліс, вплив коефіцієнта поперечного перекриття ε_α; для прямозубих коліс ; ; для косозубих ; ; для стальних коліс ;

К_Нα – коефіцієнт розподілу навантаження між зубами; для прямозубих коліс , для косозубих коліс К_Нα приймають за табл. 2.9;

К_Нβ – коефіцієнт нерівномірності навантаження по довжині зуба (табл. 2.6);

К_Нν – коефіцієнт динамічності навантаження (табл. 2.8).

Підставляючи у формулу (2.30) значення Z_H, Z_M, Z_ε отримують формули для визначення розрахункових контактних напружень:

– для прямозубих передач:

; (2.31)

– для косозубих передач:

, (2.32)

де F_t – в Н; d_ш, b_K – в мм; σ_н, [σ]_Н – в МПа.

Допускається перенавантаження і недовантаження . Якщо ці умови не виконуються, змінюють величину b_к не виходячи за межі рекомендованих значень Ψ_bd; якщо це не допомагає, змінюють значення міжосьової відстані a_w, вибирають інші матеріали або назначають інший вид термічної обробки і повторюють розрахунки.

_{Таблиця 2.8. Значення коефіцієнта КHV}

Передача	Твердість зубів	Колова швидкість V, м/с
		до 5	10	15	20
		Ступінь точності
		8	8	7	7
Прямозуба	До НВ 350	1,05	–	–	–
	> НВ 350	1,10	–	–	–
Косозуба і шевронна	До НВ 350	1,0	1,01	1,02	1,05
	> НВ 350	1,0	1,05	1,07	1,10

Таблиця 2.9. Значення коефіцієнта К_Hα для косозубих і шевронних передач

Ступінь точності	Колова швидкість V, м/с
	До 1	5	10	15	20
6	1,00	1,02	1,03	1,04	1,05
7	1,02	1,05	1,07	1,10	1,12
8	1,06	1,09	1,13	–	–
9	1,10	1,16	–	–	–
Примітка: Для прямозубих коліс КHα=1.

Таблиця 2.10. Значення коефіцієнта К_Нβ

	Твердість поверхні зубів
	І	ІІ	ІІІ	І	ІІ	ІІІ
0,4	1,15	1,04	1,00	1,33	1,08	1,02
0,6	1,24	1,06	1,02	1,50	1,14	1,04
0,8	1,30	1,08	1,03	–	1,21	1,06
1,0	–	1,11	1,04	–	1,29	1,09
1,2	–	1,15	1,05	–	1,36	1,12
1,4	–	1,18	1,07	–	–	1,16
1,6	–	1,22	1,09	–	–	1,21
1,8	–	1,25	1,11	–	–	–
2,0	–	1,30	1,14	–	–	–
Примітка: Графи: І – для передач з консольним розташуванням колеса відносно опор; ІІ – з несиметричним розташуванням колеса відносно опор; ІІІ – з симетричним розташуванням колеса відносно опор.

Визначають розрахункові напруження згину σ_F в основі зуба шестірні і колеса за формулами:

– для прямозубих передач:

; (2.33)

– для косозубих передач:

, (2.34)

де Y_F – коефіцієнт форми зуба, вибирають за табл. 2.11 в залежності від числа зубів z для прямозубих коліс і від числа зубів еквівалентних коліс z_V для косозубих коліс; z_V визначається за формулою:

; (2.35)

Y_β – коефіцієнт кута нахилу зуба:

– для прямозубої передачі ;

– для косозубої передачі:

; (2.36)

К_Fα – коефіцієнт, що враховує нерівномірність розподілу навантаження між зубами;

– при значенні коефіцієнта осьового перекриття:

приймають ;

– при , К_Fα визначають за формулою:

, (2.37)

де К – степінь точності передачі;

ε_α – коефіцієнт поперечного перекриття:

, (2.38)

при середньому значенні і 8-ю ступенею точності можна приймати ;

К_Fβ – коефіцієнт, що враховує нерівномірність розподілу навантаження по довжині зубів (табл. 2.12);

K_FV – коефіцієнт динамічності (табл. 2.13).

Можна знаходити напруження згину лише для менш міцного колеса, яке визначають порівнюючи характеристики міцності зубів шестірні і колеса .

Тут і , Y_Fш і Y_Fк допустимі напруження згину і коефіцієнти форми зубів шестірні і коліс.

Якщо , вибирають інше значення модуля, визначають z_ш і z_к і повторюють перевірочний розрахунок на згин.

допускається, оскільки навантажувальна здатність закритих передач обмежується контактною міцністю.

Таблиця 2.11. Коефіцієнт форми зуба Y_F для некоригованих коліс(X=0)

z або zV	17	20	22	24	26	28	30	35
YF	4,26	4,07	3,98	3,92	3,88	3,81	3,79	3,75
z або zV	40	45	50	65	80 і більше		рейка
YF	3,70	3,66	3,65	3,62	3,60		3,63

Таблиця 2.12. Значення коефіцієнта К_Fβ

Розміщення коліс відносно опор	Твердість зубів
		0,2	0,4	0,6	0,8	1,0	1,2
Консольне, опори – шарикопідшипники	≤ НВ 350	1,16	1,37	1,64	–	–	–
	> НВ 350	1,33	1,70	–	–	–	–
Консольне, опори – роликопідшипники	≤ НВ 350	1,10	1,22	1,38	1,57	–	–
	> НВ 350	1,20	1,44	1,71	–	–	–
Симетричне	≤ НВ 350	1,01	1,03	1,05	1,07	1,14	1,26
	> НВ 350	1,02	1,04	1,08	1,14	1,30	-
Несиметричне	≤ НВ 350	1,05	1,10	1,17	1,25	1,42	1,61
	> НВ 350	1,09	1,18	1,30	1,43	1,73	-

_{Таблиця 2.13. Орінтовне значення коефіцієнта КFV}

Степінь точності	Твердість зубів	Швидкість V, м/с
		До 3	3…8	8…12,5
6	≤ НВ 350	1/1	1,2/1	1,3/1,1
	> НВ 350	1/1	1,15/1	1,25/1
7	≤ НВ 350	1,15/1	1,35/1	1,45/1,2
	> НВ 350	1,15/1	1,25/1	1,35/1,1
8	≤ НВ 350	1,25/1	1,45/1,3	-/1,4
	> НВ 350	1,20/1	1,35/1,2	-/1,3
Примітка: В чисельнику КFV – для прямозубих передач, в знаменнику – для косозубих.