5.Расчет режимов деформации при прокатке листов

5.1.Методики расчета режимов обжатий

Современными методами расчета, имеющими теоретические толкования, являются:

1. расчет по предельным углам захвата;

2. расчет по использованию полной мощности электродвигателей, если есть запас по прочности валков и прочности передаточных механизмов;

3. расчет, основанный на равенстве полных давлений металла на валки в каждом проходе;

4. по прочности валков (если обеспечивает N двигателя)

5. расчет режимов обжатий по М_кр двигателя;

6. расчет режимов прокатки с учетом энергосиловых и прочностных характеристик оборудования и особенностей технологии;

7. Расчет по коэффициентам высотной деформации;

8. расчет по величине относительной деформации;

9. расчет режимов деформации при прокатке толстолистовой стали с задачей раската «на угол»

10. расчет по кривым удельного расхода энергии на 1 тонну проката листовой стали;

11. расчет, основанный на использовании пластичности металла.

Рассмотрим подробнее некоторые из этих методик

5.2.Расчет по коэффициентам высотной деформации

Обычно на любом листопрокатном стане известны размеры исходного листа (сляба) и/или конечного профиля. Для расчета обжатий задаются величины обжатия в первом и последнем проходах Δh_min и Δh_max (по ходу прокатки) исходя из условия захвата металла валками, мощности электродвигателя, прочности валков и др. определяют коэффициент высотной деформации и .

Иногда поступают так, задают или определяют величину среднего обжатия

после, зная величину суммарного обжатия , определяют число проходов

Общий коэффициент высотной деформации

средний коэффициент высотной деформации

В первом проходе

.

или Δh₁, Δh_n, тогда

или

А затем

Из практики известно, что величина уменьшается по ходу прокатки (Рис. 5 .63), что обусловлено потерей металлом пластичности, уменьшением толщины полосы и т.п. Приняв линейный закон изменения коэффициента высотной деформации. При этом для сохранения закономерности делают так:

т.к. , то , при этом C > 1, а затем

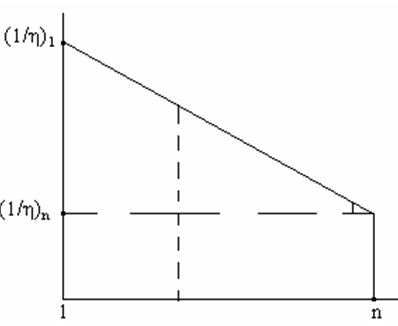
Рис. 5.63. Изменение величины 1/η по проходам

Алгоритм расчета по коэффициентам высотной деформации

1. Задают Δh₁ ( например из условия прочности валков или предельных углов захвата)

2. Задают Δh_n ( например, 10…20% от h_n)

3. ;

4. или

5. 

6. 

7. Строим график

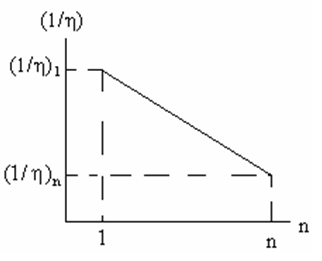
8. Считаем

   1. Если по ходу прокатки

, h₀, Δh₁ – известны, .

Определяем h₂: ; , – из графика,

2. Если против хода прокатки

, h_n, Δh_n – известны

; ; ;

Можно и так

3.

4.

5.

6. ; ; ;

7. Строим график

8. Считаем , можно при построении.

   1. Если на графике соблюдать следующее

тогда , а раз принят линейный закон, то , следовательно (или наоборот идти от )

8. Второй вариант (чтобы не задавать Δh_n по  или др.).

Задаем Δh₁ и Δh_с имея h₀ и h_n.

Считаем ; .

Строим график имея ввиду . ; ; ; ;

10. При прокатке толстолистовой стали на одно- или двухклетьевых станах с прокаткой в поперечном направлении до получения необходимой ширины на графике строят две линии (или два графика) – одна(один) для коэффициента высотной деформации при прокатке в поперечном направлении, вторая – при продольной прокатке.

H, B – размеры сляба, h, b – размеры листа

Если B < b, то делают поперечную прокатку или прокатку «на угол», а если B = b, то считают по вышеописанной методике.

1. для раскатки сляба в поперечном направлении на ширину листа.

, здесь – неизвестно Δb ≈ 0, то есть .

2. Находим толщину для получения нужной ширины (в I этапе получения раската)

3. Находим . Теперь в I этапе (поперечной прокатки) известно h₀,  поступают как сказано ранее: задаем , , далее , , n^I и строим график для поперечной раскатки (I этап)

4. Находим Δh_Σ после горизонтальной кантовки и прокатки до конечной толщины

Теперь как для второго этапа известны и , а дальше как говорили.

Важным моментом является определение величины обжатия в I проходе. Часто используется условие прочности валков.

Тогда

где р_с – среднее удельное давление, принимаемое по опытным данным (например Литовченко или Григорян), так для толстого листа р_с ≈ 100 МПа;

Р – усилие прокатки.

где [_изг] – принимается в зависимости от материала и способа изготовления валков, для стальных валков [_изг] = 120…140 МН (Литовченко)

L – длина бочки валка;

l – длина шейки валка.

Ограничения.

По , Р, М, ресурс пластичности.

Пример: разработать режимы из листа 2,5 мм до листа 0,8 мм.

Δh₁ = 0,9 мм.

Δh_n = 0,15 мм.

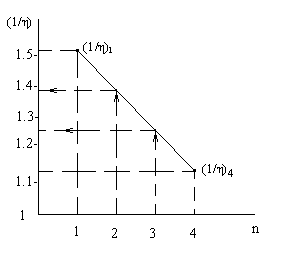
1.38; Δh₂= ; h₂=

1.24; Δh₃= ; h₃=

