4.4.1.Эмпирические методы расчета формоизменения

Различают следующие подходы в этой группе методов:

• по ходу прокатки;

• против хода прокатки;

• комбинированный метод.

4.4.1.1Расчет по ходу прокатки

Рис. 4.60. К расчету по ходу прокатки

Расчет выполняется в следующей последовательности.

В первом проходе задаём обжатие Δh₁ и определяем высоту полосы . Находим уширение Δb по какой-либо методике, и находим ширину полосы . Определяем площадь поперечного сечения полосы S₁ в зависимости от ее размеров и формы. Находим коэффициент вытяжки в первом проходе .

Во втором проходе задаём или считаем Δh₂. Определяем высоту полосы во втором проходе при наличии кантовки или без кантовки . Вычисляем уширение и находим ширину полосы при наличии кантовки или без кантовки .

Если во втором проходе не получились желаемые размеры, то корректируем обжатие в предыдущем или данном проходе.

Аналогично первому проходу определяем площадь поперечного сечения полосы S₂ и коэффициент вытяжки λ₂ во втором проходе.

Дальнейший расчет ведется аналогично описанному сценарию.

4.4.2.Расчет формоизменения с использованием законов механики деформированного тела

Данный метод расчета формоизменения основан на методике расчета калибровки УПИ для чередующихся равноосных и неравноосных калибров.

Существует два алгоритма расчета.

4.4.2.1Алгоритм 1

Заданы два равноосных сечения, необходимо найти размеры неравноосного сечения, находящегося между ними (Рис. 4 .61).

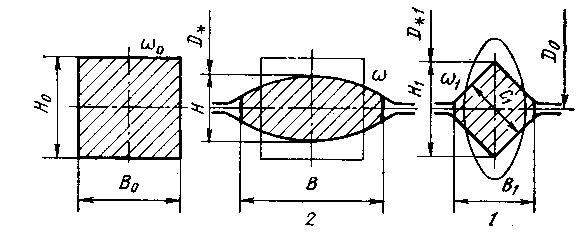
Рис. 4.61. Калибровка валков по схеме равноосное сечение – неравноосное сечение – равноосное сечение

Дано: h₀, b₀, S₀; h₁, b₁, S₁; D₀, n_в, t₀.

Находим приведенный диаметр валков и суммарную вытяжку в двух проходах

По номограмме λ_Σ = λ(А₁, а, α) находим а и α.

По номограмме λ₁ = λ(1/η₁, a, A₁) находим 1/η₁ и λ₁.

Считаем размеры неравноосной полосы и калибра при указанном коэффициенте заполнения калибра δ:

Определяем λ₂ и 1/η₂ во втором калибре

По известным формулам считаем максимально допустимые углы захвата α₁ и α₂. Находим также допустимые отношения сторон неравноосного сечения a_min и a_max.

Проверяем выполнение условия захвата и устойчивости:

4.4.2.2Алгоритм 2

Необходимо определить размеры большего равноосного сечения и размеры неравноосного сечения.

Находим приведенный диаметр валков по формуле

Задаем или определяем по формулам приближенные значения допустимых углов захвата в обоих калибрах и максимально допустимое отношение осей промежуточного сечения.

По номограмме λ_Σ = λ(А₁, а, α) находим допустимое значение суммарного коэффициента вытяжки. При этом находят три значения коэффициента вытяжки λ_Σa, λ_Σα₁, λ_Σα₂. Принимают наименьшее из этих значений.

Находят площадь поперечного сечения исходной равноосной полосы:

По формулам для определения площади поперечного сечения считают размеры большего равноосного сечения полосы:

Определяют коэффициент деформации и размеры промежуточного сечения полосы по предыдущей методике.

Проверяем выполнение условия захвата и устойчивости по выражениям :

4.4.3.Расчет формоизменения, основанный на методах приведения

Существует четыре метода приведения фасонных полос к прямоугольной форме:

1. Метод соответственной полосы.

2. Метод приведенной полосы.

3. Метод описанных прямоугольников.

4. Метод эквивалентной полосы.

Рассмотрим каждый метод подробней

4.4.3.1Метод соответственной полосы

Считаем, что площадь соответственной полосы равна площади реальной полосы:

Считаем также, что отношения сторон равны:

Тогда получаем

Отсюда

4.4.3.2Метод приведенной полосы

Считаем, что площадь приведенной полосы равна площади реальной полосы:

Считаем также, что ширины равны:

Тогда получаем

4.4.3.3Метод описанных прямоугольников

Размеры полосы принимаются равными габаритным размерам полосы, а площадь - произведению высоты на ширину.

4.4.3.4Метод эквивалентной полосы

Ширина эквивалентной полосы равна ширине приведенной полосы

Высота эквивалентной полосы

или

4.5.Конструирование калибров

Калибры простой формы и их основные размеры показаны на Рис. 4 .62.

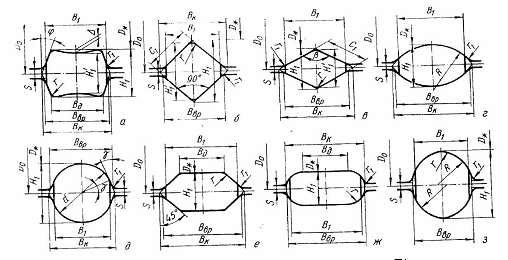
Рис. 4.62. Калибры простой формы

Соотношение геометрических размеров в калибрах простой формы приведены в Таблица 4 .5

Таблица 4.5

Геометрические соотношения в калибрах простой формы

Форма калибра

Формулы и зависимости

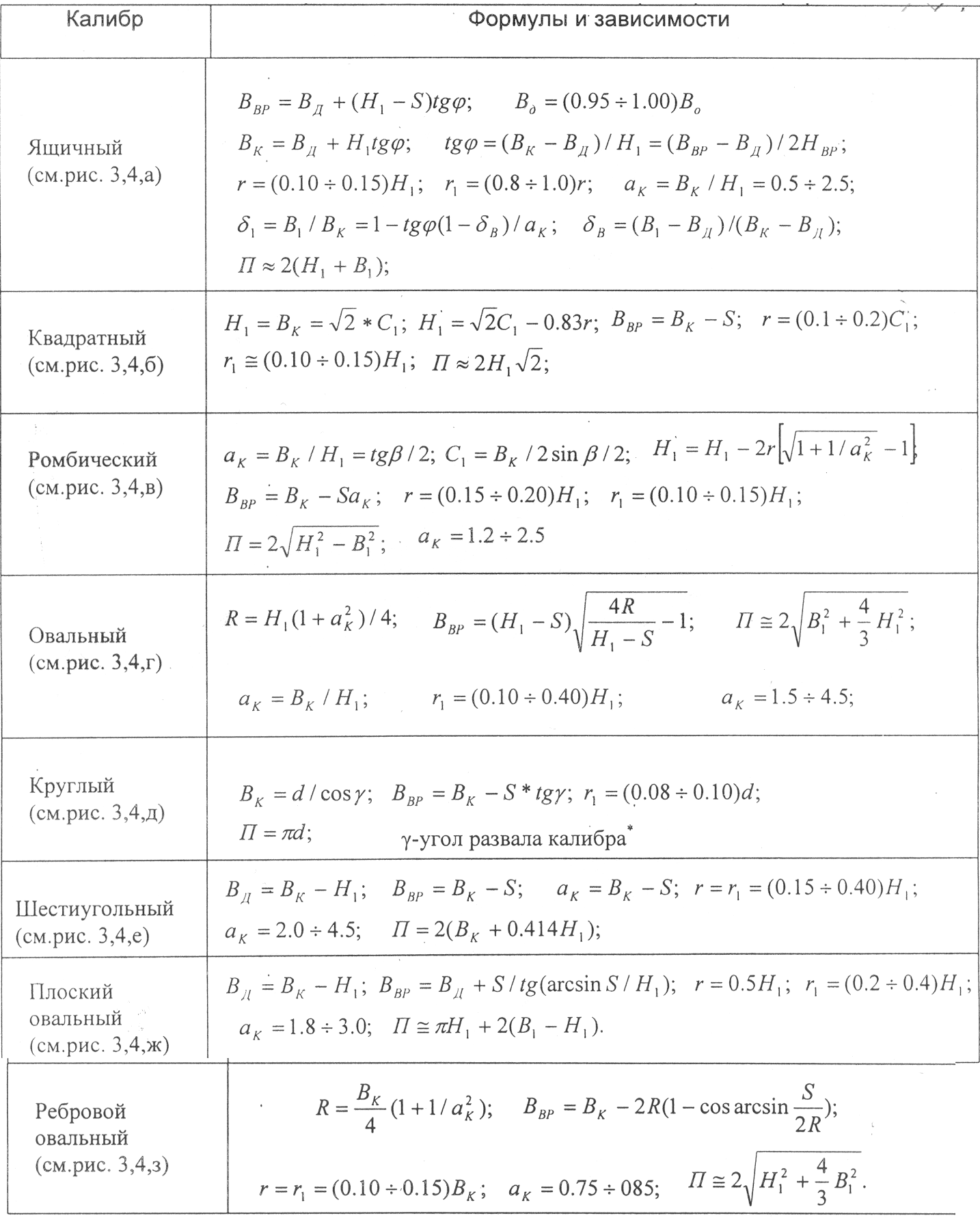
Таблица 4.6

Зависимость угла γ для чистового круглого калибра от его диаметра

Диаметр круга, мм

Угол γ