
- •Тема №1
- •Тема №2
- •Тема № 3.
- •Тема № 4
- •Связь функции тока с потенциалом скорости
- •Комплексная скорость и комплексный потенциал
- •Тема № 5
- •Функция тока.
- •Связь функции тока с потенциалом скорости.
- •Комплексная скорость и комплексный потенциал.
- •Подъёмная сила .
- •Тема №6
- •Гипотеза о пограничном слое.
- •Тема №7
Тема №1
Наименование раздела |
Содержание раздела |
Вводные сведения. Основные физические свойства жидкостей и газов. Общие законы и уравнения статики, кинематики и динамики сплошных сред. |
Основные понятия и определения. Параметры потока. Свойства жидкостей, газов и паров. Основные термодинамические соотношения. Элементы кинематики сплошных сред. Методы изучения движения жидкости. Линии тока и вихревые линии. Деформация и вращение жидкой частицы. Теорема Гельмгольца. |
Основные понятия и определения
Жидкостью в гидравлике называют физическое тело способное изменять свою форму при воздействии на нее сколь угодно малых сил. Различают два вида жидкостей: жидкости капельные и жидкости газообразные. Капельные жидкости представляют собой жидкости в обычном, общепринятом понимании этого слова (вода, нефть, керосин, масло и.т.д.). Газообразные жидкости - газы, в обычных условиях представляют собой газообразные вещества (воздух, кислород, азот, пропан и т.д.).
Основной отличительной особенностью капельных и газообразных жидкостей является способность сжиматься (изменять объем) под воздействием внешних сил. Капельные жидкости (в дальнейшем просто жидкости) трудно поддаются сжатию, а газообразные жидкости (газы) сжимаются довольно легко, т.е. при воздействии небольших усилий способны изменить свой объем в несколько раз.
В гидравлике рассматриваются реальная и идеальная жидкости. Идеальная жидкость в отличие от реальной жидкости не обладает внутренним трением, а также трением о стенки сосудов и трубопроводов, по которым она движется. Идеальная жидкость также обладает абсолютной не сжимаемостью. Такая жидкость не существует в действительности, и была придумана для облегчения и упрощения ряда теоретических выводов и исследований.
Вязкость (внутреннее трение) — одно из явлений переноса, свойство текучих тел (жидкостей и газов) оказывать сопротивление перемещению одной их части относительно другой. В результате происходит рассеяние в виде тепла работы, затрачиваемой на это перемещение.
Теплоемкость. Остановимся на следующей аномалии воды, которая связана с ее теплоемкостью. Теплоемкость воды сама по себе не аномальна, но она в 5-30 раз выше, чем у других веществ. (Только водород и аммиак обладают большей, чем вода теплоемкостью). У всех тел, кроме ртути и жидкой воды, удельная теплоемкость с повышением температуры возрастает. У воды же удельная теплоемкость в интервале, температур от 0 до 35 °С падает, а затем начинает возрастать. Удельная теплоемкость воды при 16 °С условно принята за 1 и служит, таким образом, эталоном меры для других веществ. Как и плотность, удельная теплоемкость воды в зависимости от температуры не однозначна, а двузначна. Например, при 25 и при 50 °С она одинакова - 0,99800 кал/(г•°С). Теплоемкость льда на интервале от 0 до минус 20 °С в среднем 0,5 кал/(г•°С), т. е. в два раза меньше, чем у жидкой воды. Удельная теплоемкость спирта и глицерина - 0,3 (в три раза меньше, чем у воды), железа - 0,1, платины - 0,03, дерева - 0,6, а каменной соли и песка - 0,2 кал/ (г•°С). В связи со сказанным выше становится понятным, почему при одинаковом получении солнечного тепла вода в водоеме нагреется в 5 раз меньше, чем сухая песчаная почва на берегу, но при этом вода во столько же раз дольше будет сохранять тепло, нежели песок. Любопытно, что теплоемкость воды в переохлажденном состоянии (например, при -7,5 °С) на 2% выше, чем при той же температуре, но уже в кристаллическом состоянии.
Теплопрово́дность — это процесс переноса внутренней энергии от более нагретых частей тела (или тел) к менее нагретым частям (или телам), осуществляемый хаотически движущимися частицами тела ( атомами, молекулами, электронами и т.п.). Такой теплообмен может происходить в любых телах с неоднородным распределением температур, но механизм переноса теплоты будет зависеть от агрегатного состояния вещества. Явление теплопроводности заключается в том, что кинетическая энергия атомов и молекул, которая определяет температуру тела, передаётся другому телу при их взаимодействии или передаётся из более нагретых областей тела к менее нагретым областям. Иногда теплопроводностью называется также количественная оценка способности конкретного вещества проводить тепло.
Температуропроводность (коэффициент температуропроводности) — физическая величина, характеризующая скорость изменения (выравнивания) температуры вещества в неравновесных тепловых процессах. Численно равна отношению теплопроводности к объёмной теплоёмкости при постоянном давлении, в системе СИ измеряется в м²/с.
![]() ,
,
где ![]() —
температуропроводность,
—
температуропроводность, ![]() — теплопроводность,
— теплопроводность, ![]() — изобарная удельная
теплоёмкость, ρ — плотность
— изобарная удельная
теплоёмкость, ρ — плотность
Температуропроводность и теплопроводность являются двумя из наиболее важных параметров веществ и материалов, поскольку они описывают процесс переноса теплоты и изменение температуры в них.
Величина коэффициента температуропроводности зависит от природы вещества. Жидкости и газы обладают сравнительно малой температуропроводностью. Металлы, напротив, имеют бо́льший коэффициент температуропроводности.
Свойства жидкостей, газов и паров
Переход вещества из жидкого или твердого состояния в газообразное называется парообразованием. Различают следующие виды парообразования: испарение и кипение.
Парообразование со свободной поверхности жидкости называется испарением, с поверхности твердого тела - сублимацией или возгонкой.
Вследствие теплового движения молекул испарение возможно при любой температуре, но с возрастанием температуры скорость испарения увеличивается.
При переходе из жидкости в пар молекулы должны преодолеть силы молекулярного сцепления в жидкости. Работа против этих сил, а также против внешнего давления уже образовавшегося пара совершается за счет кинетической энергии теплового давления молекул. В результате испарения жидкость охлаждается. Чтобы процесс испарения протекал при постоянной температуре, необходимо жидкости сообщать тепло.
Физическая величина, показывающая какое количество теплоты необходимо, чтобы обратить жидкость массой 1 кг в пар без изменения температуры, получила название удельной теплоты парообразования:
[L]=1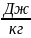
1 джоуль на килограмм равен удельной теплоте парообразования жидкости, имеющей при массе 1 кг теплоту парообразования 1Дж, если температура жидкости не меняется.
Q = Lm - теплота, необходимая для превращения жидкости массой m в пар без изменения температуры.
Переход вещества вследствие его охлаждения или сжатия из газообразного состояния в жидкое или твердое называется конденсацией. Конденсация пара возможна только при температуре ниже критической для данного вещества. Температура, при которой теряется различие между жидкостью и ее насыщенным паром, называется критической.
При конденсации выделяется количество теплоты, которое было затрачено на испарение сконденсировавшегося вещества.
Q = -Lm, где L - удельная теплота конденсации. Дождь, снег, роса, иней - следствия конденсации водяного пара в атмосфере.
Конденсация широко применяется в энергетике, химической технологии, в холодильной и криогенной технике, в опреснительных установках и т. д.
Процесс перехода жидкости в пар называется кипением. Оно характеризуется, в отличие от испарения, тем, что образование пара происходит не только на поверхности, но и по всей массе жидкости. При этом в объеме жидкости образуются пузырьки пара или заполненных паром полостей на нагреваемых поверхностях. Пузырьки, образующиеся при кипении, легче всего образуются на пузырьках воздуха или других газов, обычно присутствующих в жидкости.
Кипение становится возможным, если давление насыщенных паров жидкости делается равным внешнему давлению. Поэтому данная жидкость, находясь под внешним давлением, кипит при вполне определенной температуре.
Температура, при которой происходит кипение жидкости, находящейся при постоянном давлении, называют температурой кипения (tкип ).
Обычно температуру кипения приводят для нормального атмосферного давления. При увеличении давления, под которым находится жидкость, ее температура кипения повышается, при уменьшении давления - понижается. На вершине Джомолунгмы вода кипит при 72 °С.
Температура кипения при нормальном атмосферном давлении приводится обычно как одна из основных характеристик химически чистого вещества. Самой низкой температурой кипения при нормальном давлении обладает жидкий гелий (4,215 К), водород кипит при 20 К (-253 °С), кислород при 90 К (-183 °С), цинк при 1179 К (906 °С), железо при 3145 К (2872 °С).
Если жидкость свободна от газов, то образование в ней пузырьков пара затруднено. Такую жидкость можно перегреть, т. е. нагреть выше температуры кипения без того, чтобы она вскипела. Если в такую нагретую жидкость ввести ничтожное количество газа или твердых частичек, к поверхности которых прилип воздух, то она мгновенно и очень бурно закипает. Температура жидкости при этом падает до температуры кипения. Подобные явления могут служить причиной взрыва паровых котлов.
Для поддержания кипения к жидкости необходимо подводить теплоту, которая расходуется на парообразование и на работу пара против внешнего давления.
Предельной температурой кипения при изменении давления является критическая температура вещества, при которой исчезают различия в физических свойствах между жидкостью и ее насыщенным паром.
При критической температуре плотность и давление насыщенного пара становятся максимальными, а плотность жидкости, находящейся в равновесии с паром, - минимальной.
При температуре выше критической Тк вещество может находиться только в газообразном состоянии и не может быть переведено сжатием в жидкое состояние. При температурах ниже критической вещество может существовать в зависимости от давления либо в газообразном, либо в жидком состоянии, либо одновременно в виде двух фаз: жидкости и ее насыщенного пара.
Упругость насыщенных паров не может превышать критическое давление данного вещества. Объем вещества в жидком состоянии не может иметь значения больше, чем критический объем данного количества этого вещества.
При критической температуре теплота парообразования равна нулю.
Пар, находящийся в термодинамическом равновесии с жидкостью того же состава, называется насыщенным. Давление насыщенного пара зависит от температуры и рода жидкости и не зависит от объема.
Ненасыщенный пар находится при давлении, которое ниже давления насыщенного пара. В этом случае равновесие между процессами конденсации и испарения отсутствуют. Давление ненасыщенного пара зависит от температуры, объема и рода жидкости.
Основные термодинамические соотношения
Внутренняя энергия. Когда к системе подводится некоторое количество теплоты δQ, за счет этой теплоты, как было показано ранее на примере цикла Карно, может быть совершена лишь определенная работа δW, так что часть полученной тепловой энергии система теряет. Эти две величины, вообще говоря, неодинаковы, и, следовательно, система либо теряет, либо приобретает энергию, равную их разности. Предположим, что эта разность энергий остается в системе в виде т.н. внутренней энергии E. Тогда последняя увеличится от E до (E+ dE), причем
dE=δQ-δW
где δQ и δW – бесконечно малые приращения.
Вообще говоря, приращения δQ и δW не являются независимыми (почему они и обозначены здесь символом δ в отличие от приращения dE). Так, поглощение теплоты обычно сопровождается изменением объема и, следовательно, совершением работы против внешнего давления. И наоборот, если допускается расширение, то оно обычно сопровождается поглощением теплоты, отбираемой у окружающей среды. Никакие ограничения, налагаемые реально на систему, не могут полностью исключить такого взаимодействия, но мысленно можно представить себе идеальную теплоизоляцию (δQ = 0) или строго выполняющееся условие постоянного объема (δW = 0), так же как в теоретической механике вводятся понятия идеально гладких и идеально твердых тел. Только в идеальных условиях, когда δQ и δW независимы друг от друга, приращение δQ или δW можно рассматривать как полный дифференциал, тогда как их разность dE всегда является таковой.
Энтропия. Тепловая энергия δQʹ, которая не может быть преобразована в работу, пропорциональна нижней температуре T, так что можно записать δQʹ = TdS, где dS – приращение энтропии S системы. Как и E, величина S является характеристикой самой системы, а потому мы обозначаем ее приращение буквой d, а не δ.
Обозначив через δW работу, которую можно получить за счет теплоты δQ, можно написать
δW=δQ-δQʹ=δQ-TdS
Если рабочее тело в результате некоего термодинамического процесса не возвращается в исходное состояние, то значительная часть энергии оказывается бесполезной с точки зрения совершения работы, и внутренняя энергия увеличивается на соответствующую разность dE. Увеличение внутренней энергии может проявиться в изменении физического состояния рабочего тела, например в переходе из твердого в жидкое состояние (плавлении) или из жидкого в газообразное (испарении). Такая тепловая энергия называется теплотой плавления и теплотой парообразования соответственно. Повышение внутренней энергии может быть связано также с химическими изменениями (диссоциацией, разрывом связей) и даже с делением ядер.
Энтальпия. Если изменения энергии системы происходят при постоянном давлении, то, как оказывается, функция
H=E+PV
позволяет придать более простую и изящную форму уравнениям, описывающим различные процессы.
dH=dE+PdV+VdP=δQ-PdV+PdV+VdP=δQ+VdP
Следовательно, если процесс протекает при постоянном давлении (dP = 0), то выполняется равенство
dH = δQ,
т.е. подведенное количество теплоты может быть представлено в виде полного дифференциала некой величины, характеризующей внутреннее состояние системы. Эта величина называется энтальпией. Ранее она называлась тепловой функцией или теплосодержанием системы.
Свободная энергия. В изотермических условиях (dT = 0) более, чем H, удобна другая термодинамическая функция:
F=E-TS
Такие же выкладки, как и в случае энтальпии, дают dF = δW. Ранее величина F называлась свободной энергией Гельмгольца, поскольку именно Гельмгольц первым указал на ее значение, но сейчас ее называют просто свободной энергией.
Потенциал Гиббса. В тех случаях, когда изменяться могут и температура и давление, используется более общая функция
G=E-TS+PV, dG=VdP-SdT
Эту функцию иногда называют полным термодинамическим потенциалом или полезной энергией, но сейчас ее принято называть потенциалом Гиббса или гиббсовой энергией и обозначать символом G по имени Дж.Гиббса (1839–1903). Как будет показано ниже, представленные термодинамические функции позволяют определить условия, необходимые для равновесия.
В случае повышения давления на малую величину dP в системе, поддерживаемой при постоянной температуре (dT = 0), потенциал Гиббса увеличится на величину dG, а скорость его увеличения, или «чувствительность» потенциала Гиббса G к изменениям давления, дается термодинамическим выражением для объема системы
V=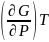
где символ частной производной указывает на то, что изменение происходит при постоянных значениях всех других параметров (в данном случае температуры T).
Точно так же чувствительность потенциала Гиббса к изменениям температуры (при постоянном давлении) есть мера энтропии системы:
T=-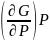
и это равенство можно рассматривать как еще одно определение энтропии.
Методы изучения движения жидкостей
В гидромеханике существуют два метода изучения движения жидкости: метод Лагранжа и метод Эйлера.
1.
Метод Лагранжа заключается в изучении
движения каждой отдельной частицы
жидкости. В этом случае движение
определяется положением частицы жидкости
в функции от времени t. Движение частицы
будет определено, если точно определить
координаты x, y, и z в заданный момент
времени t, что дает возможность построить
траекторию движения частицы жидкости.
Величины x, y, и z являются переменными
Лагранжа, а их изменения за время dt
позволяет получить значение dx, dy и dz, а
затем путь dS=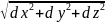 Проекции
скорости на координатные оси определяются
зависимостями,
Проекции
скорости на координатные оси определяются
зависимостями,
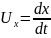 ,
,
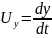 ,
,
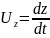 ,
а
местная скорость
,
а
местная скорость 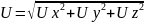
Метод Лагранжа сводится к определению семейства траекторий движения частиц движущейся жидкости.
Учитывая,
что для установления движения линии
тока совпадают с траекторией движущихся
частиц, можно записать 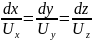
Это выражение называется уравнением линии тока. Метод Лагранжа в гидравлике не нашел широкого применения ввиду его относительной сложности.
2. Метод Эйлера основан на изучении поля скоростей, под которым понимается значение величины и скоростей во всех точках пространства, занятого движущейся жидкостью.
Переменными
Эйлера являются значения скоростей 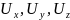 ,
которые определяются в зависимости от
координат точек пространства и времени,
т. е.
,
которые определяются в зависимости от
координат точек пространства и времени,
т. е.
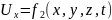
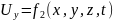
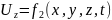
Метод Эйлера нашел широкое применение в гидравлике. Он позволяет определить скорость в любой момент времени, но в то же время не позволяет изучить движение отдельной частицы жидкости.
Рассмотрим теперь понятие расхода жидкости и средней скорости.
Расходом Q называется количество жидкости, протекающее через сечение потока в единицу времени.
dQ=Udω
или Q=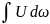
Средней скоростью называется одинаковая по всему сечению потока скорость, при которой расход равен действительному.
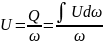
Средней скоростью в данном живом сечении потока называется такая фиктивная, но одинаковая во всех точках сечения величина, при которой через данное сечение проходит такое, же количество жидкости, как и при действии распределенных скоростей.
Линии тока и вихревые линии
Ветер, как всякий вектор, можно изобразить стрелкой, причем длина стрелки должна характеризовать числовую величину скорости, а направление — то направление, куда ветер дует. Например, в случае северо-восточного ветра стрелка должна быть направлена на юго-запад. Пространственное распределение ветра, стало быть, является векторным полем. Его можно представать графически разными способами. Наиболее наглядно поле ветра представляется с помощью линий тока, аналогичных, например, силовым линиям в магнитном поле. В каждой точке поля, в которой ветер известен, его наносят стрелкой, имеющей то направление, куда дует ветер. Затем на карте проводят линии тока так, чтобы направление ветра в каждой точке поля совпадало с направлением касательной к линии тока, проходящей через эту точку. Линии тока проводят тем ближе друг к другу, чем больше скорость ветра в данном участке поля. Таким образом, на карте получается система линий тока при первом взгляде на которую можно заключить, как именно течет воздух в данной области в данный момент. Нужно помнить, что линии тока для определенного срока наблюдений представляют собой именно моментальный снимок с поля ветра. Не следует смешивать их с путями (траекториями) воздушных частиц. Дело в том, что с течением времени поле ветра изменяется и, стало быть, меняется распределение линий тока. Каждая воздушная частица за некоторое время проделывает свой путь в меняющемся поле ветра, и поэтому ее путь не совпадает с линиями тока, построенными для одного определенного момента. Только если поле ветра установившееся, т. е. если с течением времени распределение скоростей в поле не меняется, линии тока и траектории воздушных частиц будут совпадать.
Деформация и вращение жидкой частицы
Проведенный анализ уравнений гидродинамики показывает, что их решение существенно зависит от кинематических характеристик течения, поэтому целесообразно более подробно рассмотреть кинематические характеристики движения жидкости.
Движение невязкой жидкости, содержащей вихри.
В общем случае движение твердого тела можно представить состоящим из поступательного со скоростью центра масс и вращательного вокруг мгновенной оси вращения, проходящей через центр масс. Движение жидкой частицы осложняется тем, что наряду с указанными движениями изменяется и ее форма.
Будем считать, что в любой заданный момент движения жидкости разность скоростей двух соседних элементарных ее объемов с точностью до величин первого порядка малости равна вариации скорости, т.е.
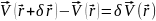
где
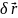 -
вариация радиуса-вектора центра масс
элементарного объема жидкости.
-
вариация радиуса-вектора центра масс
элементарного объема жидкости.
В этом случае, пользуясь правилами векторного и тензорного анализа, найдем:
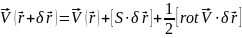
где S - тензор скоростей деформаций.
Последнее
соотношение позволяет утверждать, что
движение элементарного объема жидкости
в любой момент времени можно представить
состоящим из: а) поступательного движения
со скоростью центра масс частицы
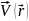 ,
б) движения, имеющего потенциал скоростей,
которое называют деформацией, в) вращения
с угловой скоростью
,
б) движения, имеющего потенциал скоростей,
которое называют деформацией, в) вращения
с угловой скоростью
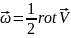
Это утверждение представляет собой так называемую первую теорему Гельмгольца , которую он сформулировал, опираясь на гидродинамические интегралы Коши.
Отметим, что Коши сделал разложение движения жидкой частицы на составляющие в несколько иной форме нежели Гельмгольц.
Жуковский, указывая на дискуссию по этому вопросу между Гельмгольцем и Бертраном, отмечал, что задача об отделении движения деформации от вращения допускает множество различных решений, пока не принята точка зрения Гельмгольца о том, что вращение есть то, что является лишним в движении с потенциалом скоростей. В основу дальнейшего изложения положена эта точка зрения, причем соотношение (2.1) служит определением угловой скорости частицы.
Рассмотрим
поле векторов угловых скоростей
движущейся жидкости. Назовем вихревой
линией такую линию, в каждой точке
которой вектор угловой скорости совпадает
с касательной к ней. Вихревая поверхность
это совокупность вихревых линий,
проведенных через некоторый контур.
Вихревой нитью будем называть часть
жидкости, ограниченную вихревой
поверхностью, проведенной через замкнутый
контур, причем вихревую нить будем
считать элементарной, если контур
настолько мал, что в его пределах угловую
скорость можно считать постоянной.
Величину
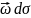 ,
где
,
где
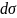 - площадь поперечного сечения элементарной
нити, называют напряжением вихря, а
величину
- площадь поперечного сечения элементарной
нити, называют напряжением вихря, а
величину
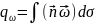 - потоком вектора напряжения вихря
сквозь поверхность
- потоком вектора напряжения вихря
сквозь поверхность
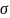 ,
причем направление единичного вектора
нормали
,
причем направление единичного вектора
нормали
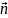 к поверхности
выбрано так, чтобы косинус угла между
векторами
и
к поверхности
выбрано так, чтобы косинус угла между
векторами
и
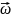 был бы положительным.
был бы положительным.
Теорема Гельмгольца
Пусть F — векторное поле в R³, и пусть оно дважды непрерывно дифференцируемо и убывает быстрее чем 1/r на бесконечности в случае неограниченной области. Тогда поле F представимо в виде суммы безвихревого поля (ротор которого равен нулю) и соленоидального поля (дивергенция которого равна нулю).
Одно из возможных представлений для векторного поля F в такой форме имеет вид суммы градиента и ротора двух явно вычислимых функций, как написано ниже:
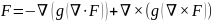
где g— это оператор ньютониан (если он действует на векторное поле вроде ∇ × F, он действует на каждую его компоненту).
Если F имеет нулевую дивергенцию, ∇·F = 0, то F называется соленоидальным или бездивергентным, и разложение Гельмгольца поля F сокращается до
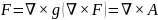
В случае такого представлении поля A называется векторным потенциалом поля F. Для соленоидального поля (то есть поля с нулевой дивергенцией) всегда можно построить вектор-функцию (векторный потенциал), ротором которого данное поле является. Векторный потенциал для заданного соленоидального поля определяется со значительной степенью свободы. В частности, без ограничения общности на него можно наложить условие кулоновской калибровки (или нормировки) ∇·A = 0 (частный случай бездивергентного векторного потенциала, см. также ниже задачу о восстановлении вектор-функции по ротору и дивергенции). К векторному потенциалу можно свободно добавить градиент любой скалярной функции — от этого его ротор, то есть определяемое им соленоидальное поле, не меняется (а если указанная скалярная функция удовлетворяет уравнению Лапласа, то не меняется также и условие кулоновской калибровки, когда векторный потенциал ему удовлетворяет).
В случае, если F имеет нулевой ротор, ∇×F = 0, то F называется безвихревым или локально потенциальным полем, а разложение F принимает вид
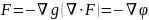
В случае такого представления поля φ называется скалярным потенциалом поля F. Для безвихревого поля (то есть поля с нулевым ротором) всегда можно построить скалярную функцию (скалярный потенциал), градиентом которого данное поле является. Скалярный потенциал для заданного безвихревого поля определяется с точностью до аддитивной константы.
В общем случае F представимо суммой
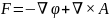 ,
,
где отрицательный градиент скалярного потенциала — безвихревая компонента поля, а ротор векторного потенциала — соленоидальная. Представление F в виде суммы безвихревого поля и соленоидального поля не является единственным, поскольку к φ всегда можно прибавить произвольную функцию ψ, удовлетворяющую уравнению Лапласа, а к A — согласованную с ψ вектор-функцию H, являющуюся результатом решения задачи о восстановлении вектор-функции по ротору и дивергенции (см. ниже) в соответствии с уравнениями ∇·H = 0, ∇×H = ∇ψ. Такая подстановка не только меняет скалярный и векторный потенциалы, участвующие в разложении Гельмгольца, но и существенным образом меняет безвихревое поле -∇(φ+ψ) и соленоидальное поле ∇×(A+H), на сумму которых распадается поле F.
