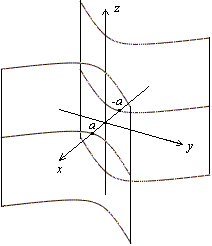
1. Визначення цп.

Припустимо задана пряма з направляючим вектором і лінія , не колінеарний площині . Пряма визначає невласний пучок паралельних прямих. Множина Ф всіх точок простору, які належать тим прямим пучка, які перетинають лінію , називається циліндричною поверхнею (ЦП).

Лінія називається направляючою, пряма - твірною ЦП. . вводячи в просторі афінну систему координат , враховуючи, що вектор має координати можна вивести рівняння ЦП , де точка .

Якщо твірна ЦП Ф паралельна осі , то і рівняння співпадає з рівнянням направляючої , тобто .

Якщо в рівнянні відсутня одна з координат, то це рівняння визначає ЦП з твірною, паралельною координатній осі, чия координата відсутня.

Поверхні обертання другого порядку
Назва поверхні	Канонічне рівняння	Зображення
Еліпсоїд - поверхня, утворена обертанням еліпса навколо однієї з осей.
Уявний еліпсоїд		відсутнє
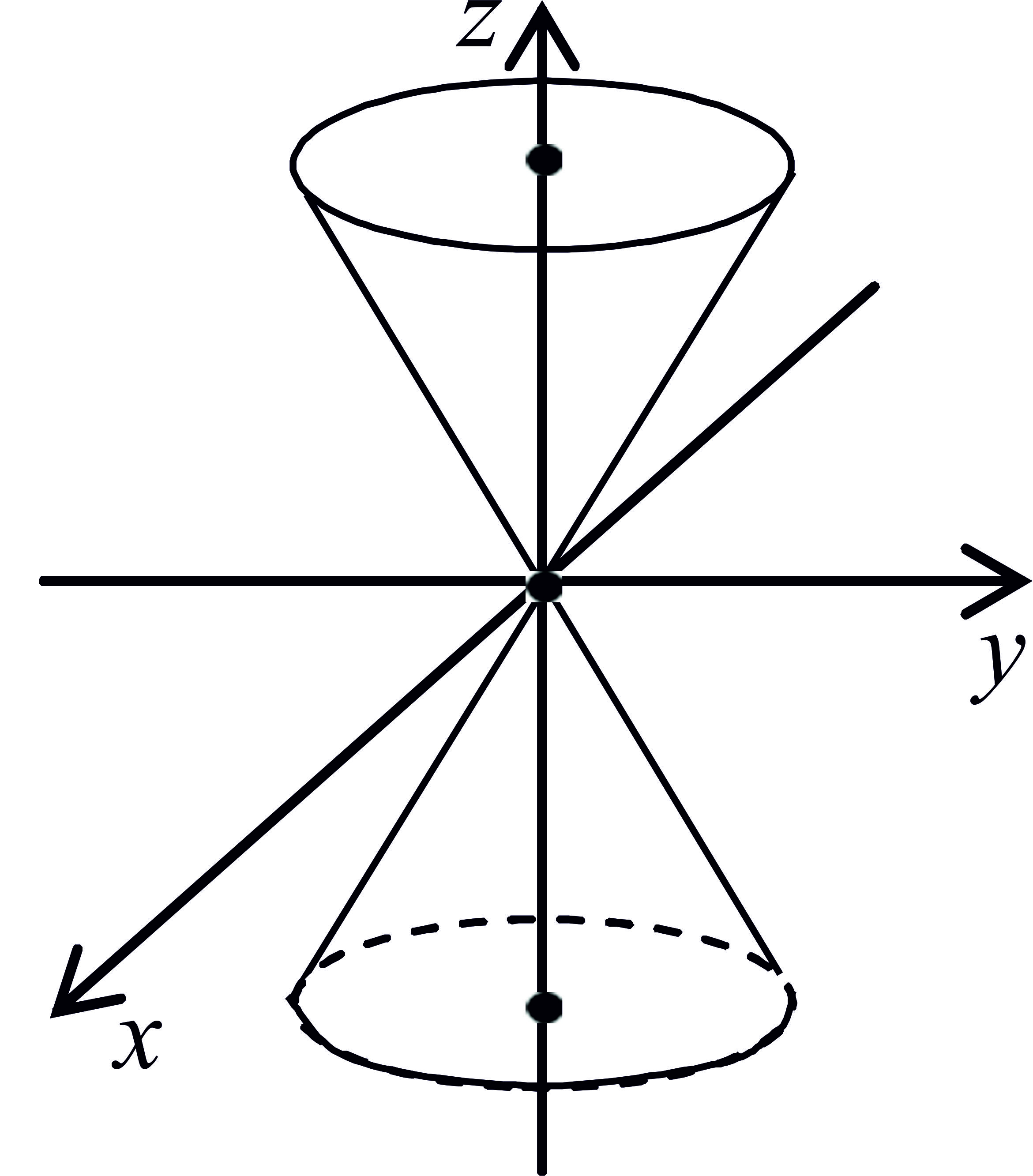
Конус - поверхня, утворена обертанням однієї прямої навколо будь-якої іншої, яка перетинає першу.
Уявний конус		відсутнє
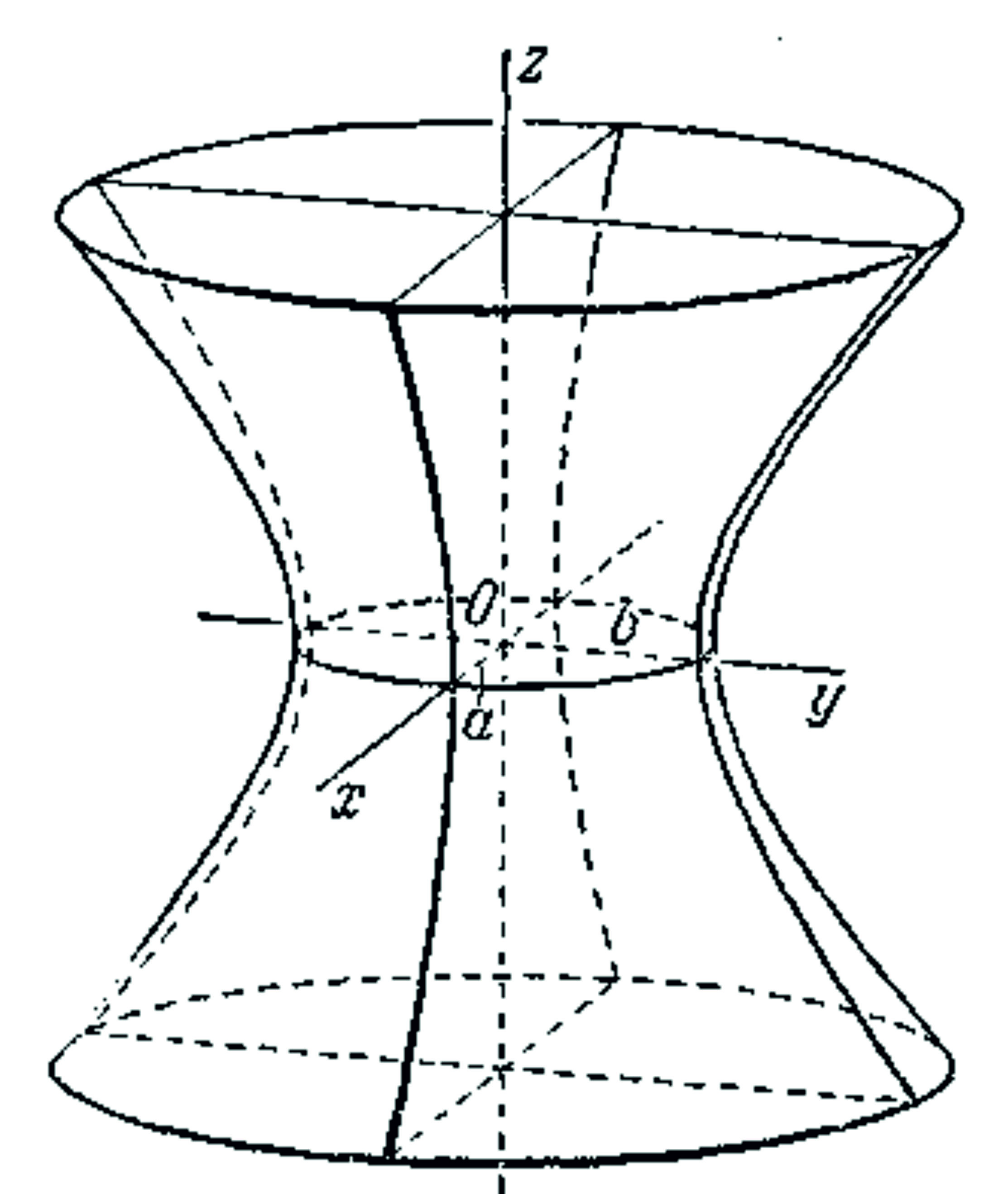
Однополосний гіперболоїд – поверхня, утворена обертанням гіперболи навколо уявної вісі.
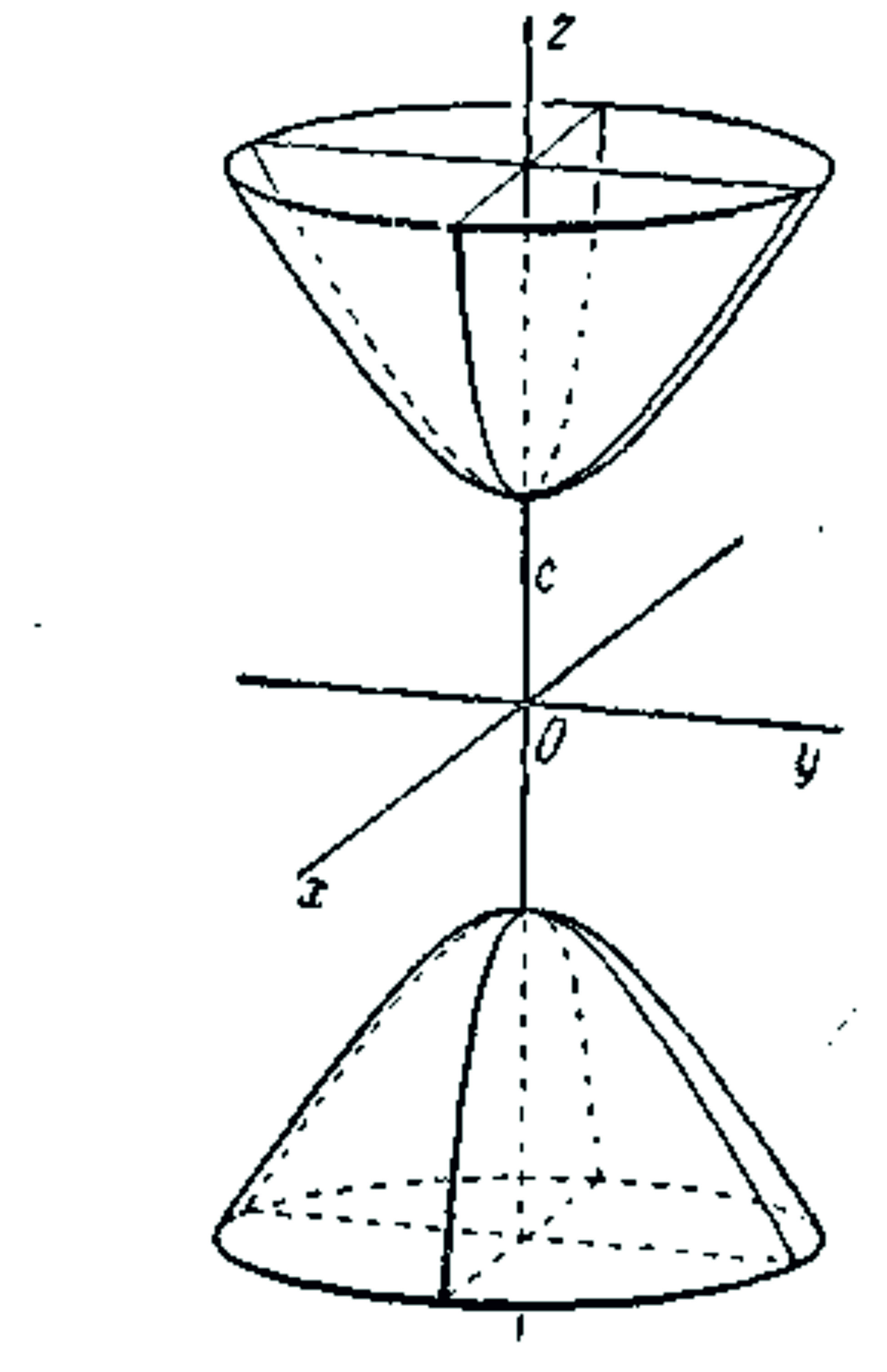
Двополосний гіперболоїд– поверхня, утворена обертанням гіперболи навколо дійсної вісі.
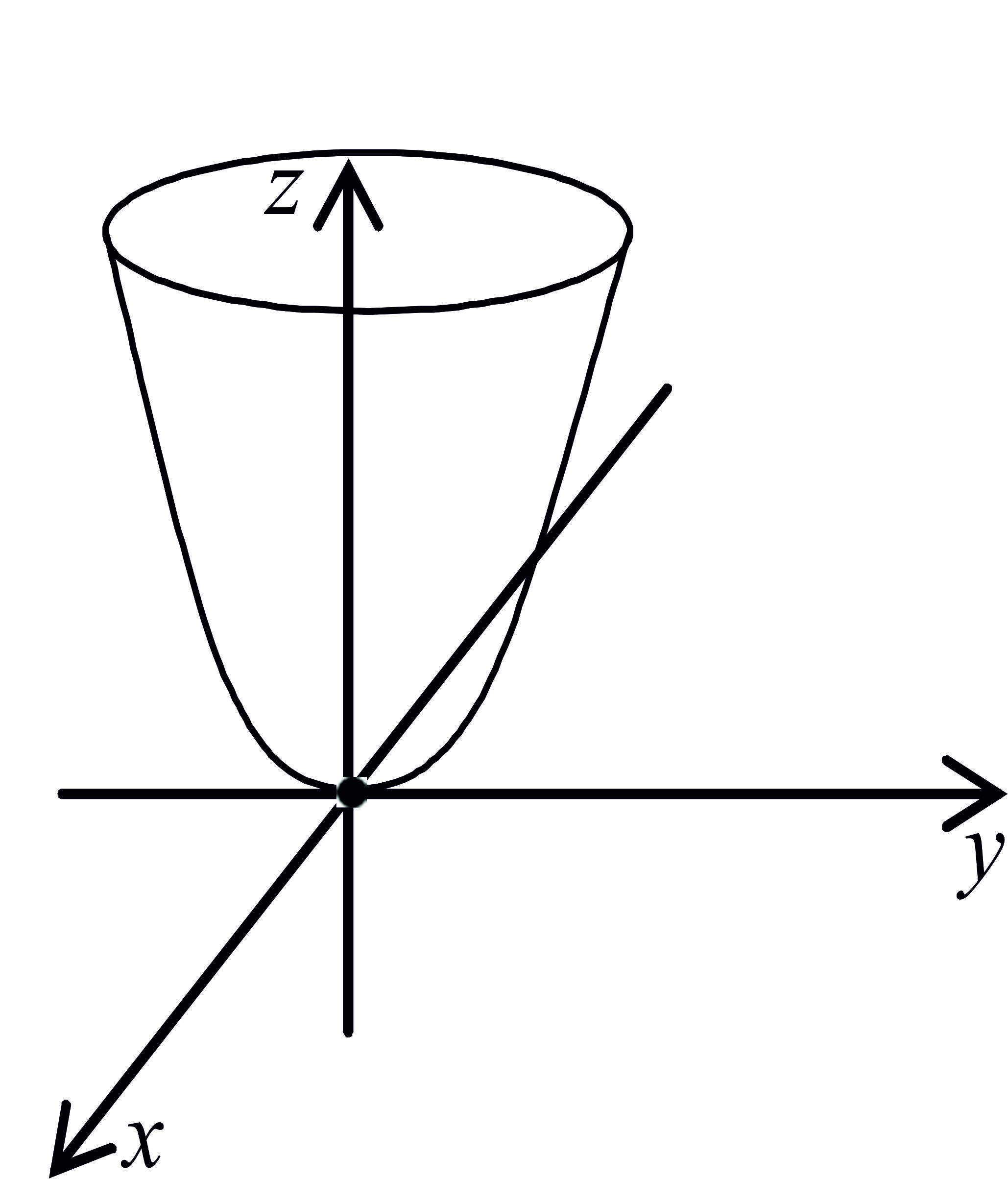
еліптичний параболоїд – називається поверхня утворена обертанням параболи навколо осі симетрії.
гіперболічний параболоїд (сідло) – це поверхня утворена при переміщенні однієї параболи вздовж іншої .
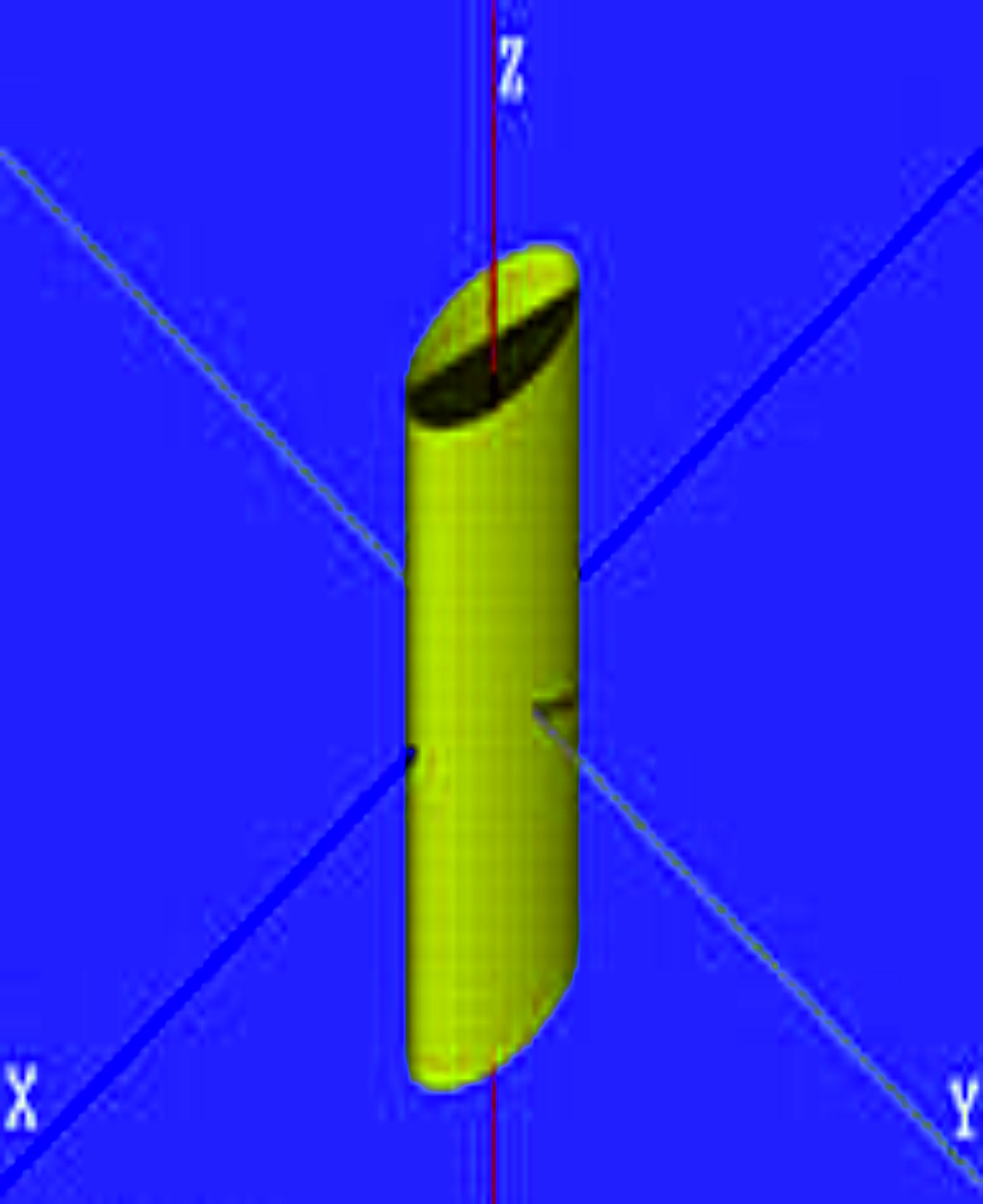
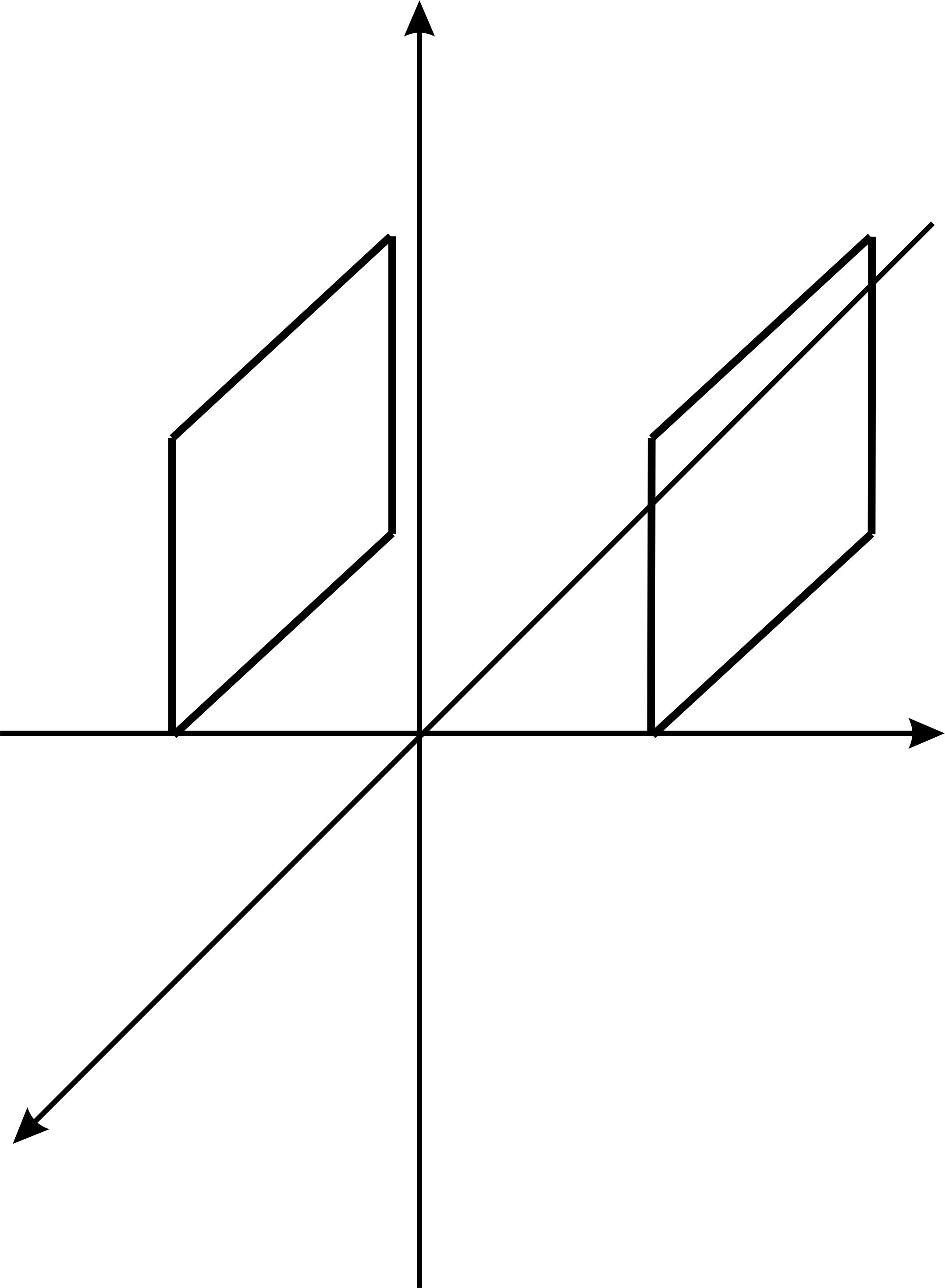
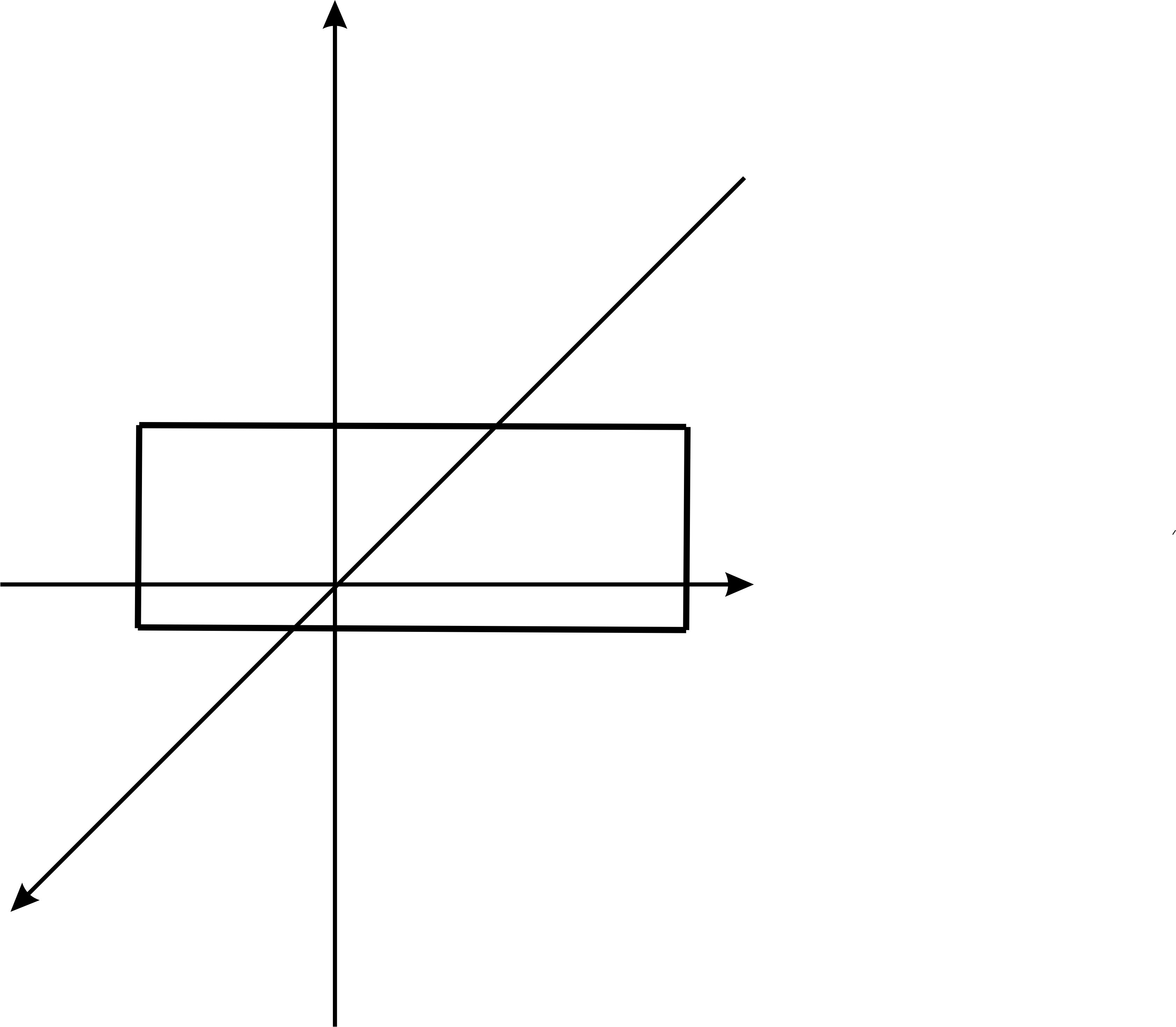
Циліндричні поверхні обертання
Еліптичний циліндр – це поверхня, утворена переміщенням еліпса вздовж осі симетрії (віссю симетрії являється вісь, відповідна змінна якої відсутня в рівнянні)
Уявний еліптичний циліндр		відсутнє
Пара уявних площин, які перетинаються по дійсній прямій		відсутнє
Гіперболічний циліндр - це поверхня, утворена переміщенням гіперболи вздовж осі симетрії (віссю симетрії являється вісь, відповідна змінна якої відсутня в рівнянні)
Пара дійсних площин, які перетинаються
Параболічний циліндр - це поверхня, утворена переміщенням параболи вздовж осі симетрії (віссю симетрії являється вісь, відповідна змінна якої відсутня в рівнянні)
Пара дійсних паралельних площин
Пара уявних паралельних площин		відсутнє
Пара площин, які співпадають

Приклади модульного завдання

Варіант №1

1. Встановити тип та зобразити поверхні а) (2б)

б) (4б)

2. З‘ясувати тип поверхні, використовуючи ортогональні інваріанти (3б)

3. Вкажіть тип поверхні, проводячи дослідження за допомогою рангів і сигнатур квадратичних форм (3б)

4. Знайти центр поверхні та записати зведене рівняння поверхні . (3б)

Варіант №2

1. Встановити тип та зобразити поверхні а) (2б)

б) (4б)

2. З‘ясувати тип поверхні, використовуючи ортогональні інваріанти (3б)

3. Вкажіть тип поверхні, проводячи дослідження за допомогою рангів і сигнатур квадратичних форм (3б)

4. Знайти центр поверхні та записати зведене рівняння поверхні (3б)

Варіант №3

1. Встановити тип та зобразити поверхні а) (2б)

б) (4б)

2. З‘ясувати тип поверхні, використовуючи ортогональні інваріанти 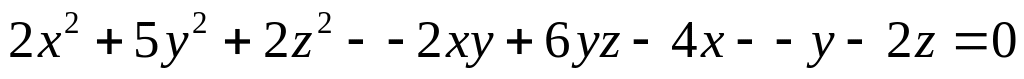(3б)

3. Вкажіть тип поверхні, проводячи дослідження за допомогою рангів і сигнатур квадратичних форм (3б)

4. Знайти центр поверхні та записати зведене рівняння поверхні (3б)

Варіант №4

1. Встановити тип та зобразити поверхні а) (2б)

б) (4б)

2. З‘ясувати тип поверхні, використовуючи ортогональні інваріанти (3б)

3. Вкажіть тип поверхні, проводячи дослідження за допомогою рангів і сигнатур квадратичних форм (3б)

4. Знайти центр поверхні та записати зведене рівняння поверхні (3б)

Індивідуальне науково – дослідне завдання

B-1	1.9	2.22	3.19	4.3	5.1	6.1	7.2
B-2	1.10	2.21	3.17	4.7	5.2	6.3	7.4
B-3	1.11	2.20	3.15	4.9	5.3	6.5	7.6
B-4	1.12	2.19	3.13	4.5	5.4	6.7	7.8
B-5	1.13	2.18	3.11	4.1	5.5	6.9	7.10
B-6	1.14	2.17	3.9	4.11	5.6	6.11	7.12
B-7	1.15	2.16	3.7	4.18	5.7	6.13	7.14
B-8	1.16	2.15	3.5	4.13	5.8	6.15	7.16
B-9	1.17	2.14	3.3	4.20	5.9	6.17	7.18
B-10	1.18	2.13	3.1	4.15	5.10	6.19	7.20
B-11	1.19	2.12	3.2	4.21	5.11	6.21	7.22
B-12	1.20	2.11	3.4	4.16	5.12	6.23	7.24
B-13	1.21	2.10	3.6	4.19	5.13	6.25	7.26
B-14	1.22	2.9	3.8	4.17	5.14	6.27	7.28
B-15	1.23	2.8	3.10	4.2	5.15	6.29	7.30
B-16	1.24	2.7	3.12	4.16	5.16	6.30	7.3
B-17	1.25	2.6	3.14	4.14	5.17	6.2	7.5
B-18	1.26	2.5	3.16	4.12	5.18	6.4	7.7
B-19	1.27	2.4	3.18	4.10	5.19	6.6	7.9
B-20	1.28	2.3	3.20	4.8	5.20	6.8	7.11
B-21	1.29	2.2	3.21	4.6	5.21	6.10	7.1
B-22	1.30	2.1	3.22	4.4	5.20	6.12	7.13
Сторінка	cтр. 2-3	cтр. 4-5	cтр. 6	стр.7	стр. 8-9	стр.10 - 12	стр.12

1. Скласти канонічні рівняння: а) еліпса; б) гіперболи; в) параболи (А, В  точки, лежачі на кривій, F фокус, а  велика (дійсна) полу вісь, b мала (уявна) полу вісь,  ексцентриситет, y= ±kx  рівняння асимптот гіперболи, D директриса кривої, 2с  фокусна відстань).

1.1. а) b=15,F(-10,0); б)a=13 =14/13; в) D: x= - 4.

1.2.а) b=2, F(4 ,0); б) a= 7= /7; в) D: x= 5.

1.3. а) А(3, 0), В(2, /3); б)k= 3/4, = 5/4; в)D: y= -2.

1.4.а)= /5, А(-5,0); б)А( , 3), В(4 , 3 ); в)D: y=1.

1.5.а) 2а= 22, = /11; б) k= 2/3, 2с=10 ; в)вісь симетрії Ох і А(27, 9).

1.6.а) b= , = /25; б)k= 3/4, 2a= 16; в)вісь симетрії Ох і А(4, -8).

1.7. а) а=4, F(3, 0); б)b=2 , F(-11, 0); в)D: x= -2.

1.8. а) b=4,F(9,0); б) a=5=7/5; в) D: x= 6.

1.9.а) А(0, ), В( , 1); б)k= /10, = 11/10; в)D: y= -4.

1.10.а)=7/8, А(8,0); б)А(3,- ), В( , 6); в)D: y= 4.

1.11. а) 2а= 24, = /6; б) k= , 2с=10; в)вісь симетрії Ох і А(-7, -7).

1.12. а) b= 2, = 5 /29; б)k= 12/13, 2a= 26; в)вісь симетрії Ох і А(-5, 15).

1.13. а) а=6, F=(-4, 0); б)b=3, F(7, 0); в)D: x= -7.

1.14.а) b=7,F(5,0); б) a=11=12/11; в) D: x= 10.

1.15.а) А(- ,1/3), В( /2, 1/2 ); б) k= 1/2, = /2; в)D: y= -1.

1.16. а)=3/5, А(0,8); б)А( , 0), В(-2 , 1); в)D: y= 9.

1.17.а) 2а= 22, = 10/11; б) k= /5, 2с=12; в)вісь симетрії Ох і А(-7, 5).

1.18.а) b= 5, = 12/13; б)k= 1/3, 2a= 6; в)вісь симетрії Оу і А(-9, 6).

1.19. а) а=9, F(7, 0); б)b=6, F(12, 0); в)D: x= -1/4.

1.20. а) b=5,F(-10,0); б) a=9=4/3; в) D: x= 12.

1.21.а) А(0, -2), В( /2, 1); б) k= 2 9, = 11/9; в)D: y=5.

1.22.а)=2/3, А(-6, 0); б)А( , 0), В( /3, 2); в)D: y= 1.

1.23.а) 2а= 50, = 3/5; б) k= /14, 2с=30; в)вісь симетрії Оу і А(4, 1).

1.24.а) b= 2 , = 7/8; б)k= 5/6, 2a= 12; в)вісь симетрії Оу і А(-2, 3 ).

1.25.а) а=13, F(-5, 0); б)b=44, F(-7, 0); в)D: x= -3/8.

1.26.а) b=7,F(13,0); б) b=4F(-11, 0); в) D: x= 13.

1.27.а) А(-3, 0), В(1, /3); б) k= , = /3; в)D: y=4.

1.28.а)=5/6, А(0, - ); б)А( , 1), В( , 0); в)D: y=-3.

1.29.а) 2а= 30, = 15/17; б) k= /8, 2с=18; в)вісь симетрії Оу і А(4, -10).

1.30.а) b= 2 , = 7/9; б)k= /2, 2a= 12; в)вісь симетрії Оу і А(-45, 15).

2. Записати рівняння кола, що проходить через задані точки і що має центр в точці А.

2.1.Вершини гіперболи A(0, -2).

2.2.Вершини гіперболи A(0, 4).

2.3.Фокуси гіперболи , A(0, -8).

2.4.O(0, 0), A – вершина параболи .

2.5.Фокуси еліпса , A(0, 6).

2.6.Лівий фокус гіперболи , A(0, -3).

2.7.Фокуси еліпса , A – його верхня вершина.

2.8.Вершину гіперболи A(0, -2).

2.9.Фокуси гіперболи , A(0, -4).

2.10.O(0, 0), A – вершина параболи .

2.11.Правий фокус еліпса , A(1, 7).

2.12.Лівий фокус гіперболи , A(0, 6).

2.13.Фокуси еліпса , A – його нижня вершина.

2.14.Вершину гіперболи A(0, 4).

2.15.Фокуси гіперболи , A(0, 5).

2.16.B(1, 4), A – вершина параболи .

2.17.Лівий фокус еліпса , A(-1, -3).

2.18.Ліву вершину гіперболи A(0, -6).

2.19.Фокуси еліпса , A – його верхня вершина.

2.20.Праву вершину гіперболи , A(1, 3).

2.21.Лівий фокус гіперболи , A(-1, -2).

2.22.B(2, -5), A – вершина параболи .

2.23.Правий фокус еліпса , A(2, -7).

2.24.Праву вершину гіперболи , A(-2, 5).

2.25.Фокуси еліпса , A - його нижня вершина.

2.26. Праву вершину гіперболи , A(-5, -2).

2.27.Фокуси гіперболи , A(0, -6).

2.28.B(3, 4), A – вершина параболи .

2.29.Лівий фокус еліпса , A(1, 8).

2.30.Правий фокус гіперболи , A(2, 8).

3. Побудувати криву, задану рівнянням в полярній системі координат.

3.1.=2sin4. 3.3. =2sin2. 3.5. =2/(1+cos). 3.7.=2(1-cos). 3.9.= 4sin3. 3.11.= 3(cos+1). 3.13.= 5(1-sin2). 3.15.= 6sin4. 3.17.= 3/(1-cos2). 3.19.= 3(1-cos4). 3.21.= 3sin4. 3.23.= 4(1+cos2). 3.25.= 4(1-sin). 3.27.= 3cos2. 3.29.= 2/(2-cos).

3.2.= 2(1-sin2). 3.4.=3sin6. 3.6.=3(1+sin). 3.8.=3(1-cos2). 3.10.=4sin4. 3.12.=1/(2-sin). 3.14.=3(2-cos2). 3.16.= 2cos6. 3.18.= 2(1-cos3). 3.20.=5(2-sin). 3.22.= 2cos4. 3.24.=1/(2-cos2). 3.26.=3(1+cos2). 3.28.= 2sin3. 3.30.= 2-cos2.

4. Визначити тип наступних рівнянь; кожне з них шляхом паралельного переносу вісей координат, привести до простого вигляду;встановити, які геометричні образи вони визначають і зобразити на кресленні,розташування цих образів відносно старих і нових осей координат:

4.1.

4.2.

4.3.

4.4.

4.5.

4.6.

4.7.

4.8.

4.9.

4.10.

4.11.

4.12.

4.13.

4.14.

4.15.

4.16.

4.17.

4.18

4.19.

4.20.

4.21.

4.22.

5. Не проводячи перетворень координат, встановити які геометричні образи визначаються наступними рівняннями:

5.1.

5.2.

5.3.

5.4.

5.5.

5.6.

5.7.

5.8.

5.9.

5.10.

5.11.

5.12.

5.13.

5.14.

5.15.

5.16.

5.17.

5.18.

5.19.

5.20.

5.21.

5.22.

5.23.

5.24.

5.25.

5.26.

5.27.

6. Побудувати поверхню і визначити її вигляд(назву):

6.1. а) б)

6.2. а) б)

6.3. а) б)

6.4. а) б)

6.5. а) б)

6.6. а) б)

6.7. а) б)

6.8. а) б)y= +3

6.9. а) б)

6.10. а) б)

6.11. а) б)

6.12. а) б)

6.13. а) б)

6.14. а) б)

6.15. а) б)

6.16. а) б)

6.17. а) б)

6.18. а) б)

6.19. а) б)

6.20. а) б)

6.21. а) б)15y =

6.22. а) б)

6.23. а) б)

6.24. а) б)

6.25. а) б)

6.26. а) б)

6.27. а) б)

6.28. а) б)

6.29. а) б)

6.30. а) б)

7. Записати рівняння і визначити вид поверхні, отриманої при обертанні даної лінії довкола вказаної вісі координат, зробити малюнок.

7.1. а) б) 9

7.2. а) б)x=1, y=2, Oz

7.3. а) б)

7.4. а) б)y=4, z=2, Ox

7.5. а) б)

7.6. а) б)

7.7. а) б)x=4, z=6,Oy

7.8. а) б)z = -1, y = 3, Ox

7.9. а) б)

7.10. а) б)

7.11. а) б)

7.12. а) б)x = 3, z = -2, Oy

7.13. а) б)

7.14. а) б)

7.15. а) б)x = -1, y = -3, Oz

7.16. а) б)

7.17. а) б)y = 2, z =6, Ox

7.18. а) б)

7.19. а) б)