
- •Теми практичних занять
- •Модуль 1 «Вектори. Операції над векторами.»
- •Лінійні операції над векторами.
- •Афінний простір. Афінна та декартова системи координат
- •Поняття пдск(прямокутна Декартова система координат)
- •Полярна система координат
- •Орієнтовані площини і простори.
- •Приклади розв’язання типових задач
- •Практичні завдання
- •Практичні завдання
- •Визначення цп.
- •Література
Практичні завдання
Практичне заняття № 6
Тема: Загальне рівняння прямої.
І. Завдання корекції знань:
1. З’ясувати, які з точок М1(3; 1), М2(2; 3), М3(6; 3), М4(— 3; —3). М5(3; —1), М6(— 2; 1) лежать на прямій 2x —3у —3 = 0 і які не лежать на ній.
2. Знайти точку перетину двох прямих
3x—4y —29 = 0, 2х + 5у + 19 = 0.
3. Сторони АВ, ВС і АС трикутника ABC дані відповідно до рівняння
4x+3у — 5 = 0, х — Зу+10 = 0, х — 2 = 0.
Визначити координати вершин цього паралелограма.
4. Сторони трикутника лежать на прямих
x+5у — 7 = 0, 3x — 2y — 4 = 0, 7x+y+19 = 0.
Вирахувати його площу S.
5. Дано рівняння двох сторін прямокутника х — 2у = 0, х — 2y+15 = 0 і рівняння однієї з його діагоналей 7x+y—15 = 0. Знайти вершини прямокутника.
6. Скласти рівняння прямої, якщо точка Р (2, 3) служить основою перпендикуляра, опущеного з початку координат на цю пряму.
7. Дано рівняння двох сторін прямокутника 5х+1у — 7 = 0, 5х + 2у — 36 = 0
і рівняння його діагоналі 3х+7у — 10 = 0.
Скласти рівняння інших сторін і другий діагоналі цього прямокутника.
8. Дано вершини трикутника A (1; - 2), B (5, 4) і С (- 2; 0). Скласти рівняння бісектрис його внутрішнього і зовнішнього кутів при вершині А.
9. Скласти рівняння прямої, що проходить через точку Р(3; 5) на одноковій відстані від точок А ( — 7; 3) і B(11; — 15).
10. Знайти проекцію точки Р( — 8; 12) на пряму, що проходить через точки A(2; — 3) і B( — 5; 1).
ІІ. Завдання для самостійного розв’язання
1. Визначити кут між двома прямими:
1) 5х—y + 7 = 0, 3x+2y = 0;
2. На прямій 3x — у — 1=0 знайти такку точку Р, різниця відстаней якої до точок A(4; 1) і B(0; 4) була б найбільшою.
3. Дана пряма 2х+3у+4 = 0. Скласти рівняння прямої, що проходить через точку M0 (2; 1):
1) параллельно данной прямой;
2) перпендикулярно до даної прямой.
Практичне заняття №7
Тема: Рівняння прямої в відрізках на осях.
І Завдання корекції знань:
1. Встановіть, які з наступних пар прямих перпендикулярні:
1) 3х — у + 5 = 0, 2) 3х — 4у + 1= 0, 3) 6х – 15у + 7= 0, 4) 9х —12у + 5 = 0
х + 3у – 1= 0; 4х — 3у + 7 = 0; 10х + 4у — 3 = 0; 8х +6y — 13 = 0;
2. Дано дві вершини трикутника М1 (—10; 2) і М2 (6; 4); його висоти пересікаються в точці N (5; 2). З’ясувати координати третьої вершини М3.
3. Дано дві вершини А (3; —1) і В(5; 7) трикутника ABC і точка N(4; —1) перетину його висот. Скласти рівняння сторін цього трикутника.
4. Скласти рівняння сторін трикутника, якщо дані одна з вершин В (– 4; – 5) і рівняння двох вершин 5х + 3у – 4 = 0 и 3x + 8y +13 = 0.
5. Скласти рівняння сторін трикутника, знаючи одну його вершину В (2; – 7), і рівняння висоти 3х + у + 11 = 0 і медіани x + 2y + 7 = 0,проведених з різних вершиню
6. Скласти рівняння прямої, яка проходить через початок координат і разом з прямими
х – у + 12 = 0, 2х + у + 9 = 0
ІІ Завдання для самостійного розв’язання
1. Скласти рівняння сторін трикутника, знаючи одну з його вершин
А (4; - 1) та рівняння двух бісектрис x – 1=0 і х – у – 1=0.
2. Скласти рівняння сторін трикутника, знаючи одну з його вершин В(2; 6), а також рівняння вершини х –7у + 15 = 0 і бісектриси 7х + у + 5 = 0, проведених з однієї вершини.
Практичне заняття №8
Тема: Кут між прямими.
І Завдання корекції знань:
1. Скласти рівняння сторін трикутника, знаючи одну його вершину С (4; – 1), а також рівняння вершини 2х – 3 + 12 = О і медіани 2х + 3y = 0, проведених з однієї вершини.
2. Скласти рівняння сторін трикутника, знаючи одну його вершину В (2; – 7), а також рівняня висоти 3х + у + 11 = 0 і медіани x + 2y + 7 = 0,
Проведених з різних вершин.
3. Скласти рівняння сторін трикутника, знаючи одну його вершину
С (4; 3), а також рівняння бісектриси x + 2у – 5 = 0 і медіани 4 + 13 y – 10 = 0,
Проведених з однієї вершини.
4. Скласти рівняння сторін трикутника, знаючи одну його вершину
А (3; – 1), а також рівняння бісектриси x – 4у+10 = 0 і медіани 6x + 10y – 59 = 0,
Проведених з різних вершин.
5. Дано дві вершини А (3; —1) і В(5; 7) трикутника ABC і точка N(4; —1) перетин його вершин. Скласти рівняння сторін цього трикутника.
ІІ Завдання для самостійного розв’язання
1. Визначити кут , утворений двома прямими:
1)
3х
– у + 5
= 0, 2) х![]() —
у
—
у![]() —
5
= 0,
—
5
= 0,
2х
+ у – 7
= 0; (3 +
)х
+ (![]() —
)у
+ 7 = 0;
—
)у
+ 7 = 0;
3) х + у – 2 = 0,
х – 3у + 3 = 0.
Розв’язати задачу, не вираховуючи кутові коефіцієнти даних прямих.
2. Довести, що через точку В (4; —5) неможливо провести пряму так, щоб відстань її від точки С(—2; 3) дорівнювала 12.
Практичне заняття №9
Тема: Нормаль до прямої. Нормальне рівняння прямої.
І Завдання корекції знань:
1. Точка А(2; —5) є вершиною квадрата, одна із сторін якого лежить на прямій
х — 2у — 7 = 0.
Визначити площу цього квадрата.
2. Сторони АВ, ВС і СА трикутника ABC відповідно дані рівняннями
х + 21у — 22 = 0, 5х — 12у + 7 = 0, 4х — 33у + 146 = 0.
Обчислити відстань від центру тяжіння цього трикутника до сторони ВС.
3. Дано вершини трикутника: А(—10; —13), В(—2; 3) і С(2; 1). Обчислити довжину перпендикуляра, опущеного з вершини В на медіану, проведену з вершини С.
4.Довести, що пряма 2х —3у+6 = 0 не перетинає відрізок, обмежений точками
М1(—2; —3) і М2(1; —2).
5. Дві сторони квадрата лежать на прямих 5х — 12у — 65 = 0, 5х — 12у + 26 = 0.
Обчислити його площу.
6. Дано три паралельні прямі 10х+15у —3 = 0, 2х+3у + 5 = 0, 2х+3у —9 = 0.
Встановити, що первая з них лежить між двома іншими, і обчислити відношення, в якому вона ділить відстань між ними.
7. Дано рівняння двох сторін квадрата
5х+12у—10 = 0, 5х+12у+29 = 0.
Скласти рівняння двох інших його сторін за умови, що точка M1(—3; 5) лежить на стороні цього квадрата.
ІІ Завдання для самостійного розв’язання
1. Обчислити відстань d між паралельними прямими кожному з наступних випадків:
1) 3х —4у—10 = 0, 2) 5х—12у + 26 = 0,
6х —8у + 5 = 0; 5х—12у—13 = 0;
3) 4х — 3у + 15 = 0, 4) 24х—10у + 39 = 0,
8х—6у + 25 = 0; 12х —2у —26 = 0.
2. Дано рівняння двох сторін квадрата 4х —3у + 3 = 0, 4х—3у—17 = 0 і одна із його вершин А(2; —3). Скласти рівняння двох інших сторін цього квадрата.
Практичне заняття №10
Тема: Рівняння площини у просторі І Завдання корекції знань:
1.
Скласти
рівняння площини,
яка
проходить через
точку M1(2;
1; —1) і
має
нормальний
вектор ![]() ={1,
—2; 3}.
={1,
—2; 3}.
2. Точка Р (2; —1; —1) служить основою перпендикуляра, опущений з початку координат на площину. Скласти рівняння цієї площини.
3.
Дано
дві
точки М1(3;
—1; 2) і
М2(4;
—2; —1). Скласти
рівняння площини,
яка
проходить через
точку М1
перпендикулярно
до
вектора![]() .
.
4.
Скласти
рівняння площини,
яка
проходить через
точку M1(3;
4;
—5) паралельно двом
векторам ![]() = {3; 1; —1} і
= {3; 1; —1} і
![]() =
{1; —2; 1}.
=
{1; —2; 1}.
5.
Скласти
рівняння площини,
яка
проходить через
точку M1(2;
— 1; 3) і
М2(3;
1; 2) паралельно вектору
![]() = {3; — 1; —4}.
= {3; — 1; —4}.
6. Скласти рівняння площини, яка проходить через три точки: М1 (3; — 1; 2), М2 (4; — 1; — 1) і М3 (2; 0; 2).
7. Встановити, які з наступних пар рівнянь визначають паралельні площини:
1) 2х — 3у + 5z — 7 = 0, 2х — 3у + 5z + 3 = 0;
2) 4х+2у —4z + 5 = 0, 2х + у + 2z—1=0;
ІІ Завдання для самостійного розв’язання
1. Визначити координати якого–небудь нормального вектора кожної з наступних площин. В кожному випадку написати загальний вираз координат довільного нормального вектору:
1) 3х —2у —7 = 0; 2) 5у —3z = 0; 3)х + 2 = 0;
2. Скласти рівняння площини, яка проходить через початок координат паралельно площині 5х — 3у + 2z — 3 = 0.
Практичне заняття №11 Тема: Кут між площинами.
І Завдання корекції знань:
1. Встановити, які з наступних пар рівнянь визначають перпендикулярні площини:
1) 3х—у — 2z — 5 = 0, х + 9у — 32 + 2 = 0;
2) 2х + 3у —2 —3 = 0, х — у — z + 5 = 0;
3) 2х —5у + z = 0, х + 22 —3 = 0.
2. Визначити двогранні, утворені перетином наступних пар площин:
1) 3у — z = 0, 2у + z = 0;
2) 6х + 3у — 2z = 0, х + 2у + 6z — 12 = 0;
3) х + 2у + 2z — 3 = 0, 16х+12у — 15z — 1 = 0.
3. Скласти рівняння площини, яка проходить через точку M1(3; —2; —7) паралельно площині 2х — 3z + 5 = 0.
4. Скласти рівняння площини, яка проходить через початок координат перпендикулярно двом площинам:
2х — у + 3z — 1=0, х + 2у + z = 0.
5. Скласти рівняння площини, яка проходить:
1) через вісь Ох і точку М1(4; —1; 2);
2) через вісь Оу і точку М2(1; 4; —3);
3) через вісь Oz і точку М3(3; —4; 7).
6. Скласти рівняння площини, яка проходить:
1) через точки М1(7; 2; —3) і М2(5; 6; —4) паралельно осі Ох;
2) через точки P1 (2; —1; 1) і Р2(3; 1; 2) паралельно осі Оу;
3) через точки Q1 (3; —2; 5) і Q2(2; 3; 1) паралельно осі Oz.
ІІ Завдання для самостійного розв’язання
1. Знайти точки перетину площин 2х — 3у — 4z— 24 = 0 з вісями координат.
2. Дано рівняння площини х + 2у — 3z — 6 = 0. Написати для неї рівняння «у відрізках».
3. Обчислити площу трикутника, який відсікає площину 5х—6у + 3z + 120 = 0
від координатного кута Оху.
Практичне заняття №12 Тема: Пряма у просторі. І. Завдання корекції знань:
1. Скласти рівняння прямих, утворених перетином площин 5х — 7у + 2z — 3 = 0 з координатними площинами.
2.
Знайти
точки перетину
прямої ![]() з
координатними площинами.
з
координатними площинами.
3.
Довести,
що пряма![]() перетинає
вісь Оу.
перетинає
вісь Оу.
4.
Визначити,
при якому
значенні
D
пряма![]()
перетинає: 1) вісь Ох; 2) вісь Оу; 3) вісь Oz.
5. Скласти канонічне рівняння прямої, яка проходить через дві дані точки:
(1; — 2; 1), (3; 1; —1);
6. Скласти параметричне рівняння прямої, яка проходить через точку
М1;(
—1; —3) паралельно
вектору
![]() =
{2; —3; 4};
=
{2; —3; 4};
7. Через точки M1 (—6; 6; —5) і М2(12; —6; 1) проведена пряма. Визначити точки перетину цієї прямої з координатними площинами.
ІІ. Завдання для самостійного розв’язання
1. Скласти канонічне рівняння прямої,яка проходить через дві дані точки:
(3; —1; 0),(1; 0, —3);
2. Скласти параметричне рівняння прямої,яка проходить через точку
М1;(
—1; —3) паралельно
прямій
![]()
Практичне заняття №13 Тема: Кут між прямими у просторі. І Завдання корекції знань:
1.
Визначити
косинус кута між:![]()
![]()
2.
Знайти
гострий кут між прямими :![]() ,
,
![]()
3.Довести перпендикулярність прямих:
1)
![]() і
і
![]()
2)
![]() і
і
![]()
4.Скласти
рівняння прямої,
яка
проходить через
точку М1(—
1;
2; —
3)
перпендикулярно до
вектора
![]() =
{6;
—
2;
—
3}
і
перетинає пряму
=
{6;
—
2;
—
3}
і
перетинає пряму
![]() .
.
5.Скласти
канонічне рівняння наступної прямої:
![]()
6. Дано вершини трикутника А(3; 6; —7), В(—5; 2; 3) і С(4; —7; —2). Скласти параметричні рівняння його медіани, проведеної з вершини С.
7. Дано вершини трикутника А(3; —1; —1), В(1; 2; — 7) і С(—5; 14; —3). Скласти канонічне рівняння бісектриси його внутрішнього кута при вершині В.
ІІ Завдання для самостійного розв’язання
1. Дано вершини трикутника А (2; — 1; — 3), В (5; 2; — 7) і С(—7; 11; 6). Скласти канонічне рівняння бісектриси його внутрішнього кута при вершині А.
2.
Скласти
канонічне рівняння прямої,
яка
проходить через
точку М1(1;
3;
—5) паралельно прямій
![]()
3.Скласти
канонічне рівняння наступної прямої:
![]()
Практичне заняття №14 Тема: Пряма і площина у просторі. І. Завдання корекції знань:
1.Знайти
точку перетину
прямої і площини:
![]() ,
,
![]() ;
;
2. Скласти канонічне рівняння прямої, яка проходить через точку
М0
(2;
-4; -1) і
середину відрізка
прямої
![]() заключеного
між площинами
заключеного
між площинами
![]() ,
, ![]() ,
,
3. Скласти рівняння прямої, яка проходить через точку М0 (2; — 3; — 5) перпендикулярно до площини 6х — Зу — 5z + 2 = 0.
4.
Скласти
рівняння площини,
яка
проходить
через точку
M0
(1;
—2;
1) перпендикулярно до
прямої
![]()
5.
Скласти
рівняння площини,
яка
проходить
через точку
M1(1;
2; —3)
паралельно
прямим
![]() ,
,
![]()
6. Обчислити відстань d від точки Р(2; 3; — 1) до наступних прямих:
1)
![]() ;
2)
;
2)
![]()
7. Довести паралельність прямих:
1)
![]() і
і
![]()
2)
![]() і
і
![]()
ІІ Завдання для самостійного розв’язання
1.Скласти рівняння прямої, яка проходить через точку М1(— 4; -5; 3) і перетинає дві прямі
![]()
![]() .
.
2.Скласти
рівняння площини,
яка
проходть через
точку М0(1;
—1; —1) перпендикулярно до
прямої
![]() ,
,
3.
При якому
значенні
С
пряма
![]() паралельна
площині
2x—у
+
Сz
—2
= 0?
паралельна
площині
2x—у
+
Сz
—2
= 0?
Приклади модульного завдання
Варіант №1
Рівняння прямої, яка проходить через дві точки, називається канонічним.
З загального рівняння прямої, координати нормалі (-В,А).
Якщо в загальному рівняння прямої В=0, то пряма проходить через вісь ординат.
Кут між прямими обчислюється як кут між їх нормалями.
Для того щоб прямі у просторі були паралельними, необхідно і достатньо, щоб їх направляючі вектори були колінеарні.
Відстань між прямою і точкою на площині – це проміжок між точкою і точкою на прямій.
Рівняння прямої в відрізках на осях виводиться із загального. (7б)
Задачі:
Скласти рівняння площини в відрізках на осях та зобразити її
 .
(3б)
.
(3б)Задані дві протилежні вершини квадрата А(-1,3) і С(6,2). Скласти рівняння його сторін. (6б)
Складіть загальне рівняння прямої, яка проходить через точки А(1,3,-5) В(2,-3,6). (4б)
Знайти кут між прямими
 і
і

 .
(5б)
.
(5б)
Варіант №2
Через дві точки в просторі можна провести єдину площину.
Із канонічного рівняння координати нормалі (
 ).
).Якщо в загальному рівнянні площини С=0, то площина проходить через вісь аплікат.
Якщо косинус кута між нормалями площини додатній, то кут між площинами гострий.
Дві прямі в просторі паралельні тоді і тільки тоді, коли їх направляючі вектори колінеарні.
Направляючим бівектором називається пара не колінеарних векторів, паралельних площині.
Рівняння прямої в відрізках на осях в просторі виводиться із загального. (7б)
Задачі:
Скласти рівняння медіани, бісектриси і висоти, опущені з вершини В(1,3), якщо А(1,4) і С(6,-1). (6б)
Скласти загальне рівняння прямої, яка проходить через точки А(1,3,-5) В(2,-3,6). (4б)
Зобразіть площину, яка проходить через три точки А(2,2,3), В(0,1,7) і С(0,5,8), записавши рівняння в відрізках на осях. (5б)
Обчисліть відстань від точки М(-2,-4,3) до площини
 (3б)
(3б)
Варіант №3
Дві прямі на площині перетинаються, якщо коефіцієнти при змінних в загальному рівнянню пропорційні.
Із рівняння в відрізках на осях площини точка перетину з віссю абсцис має координати (
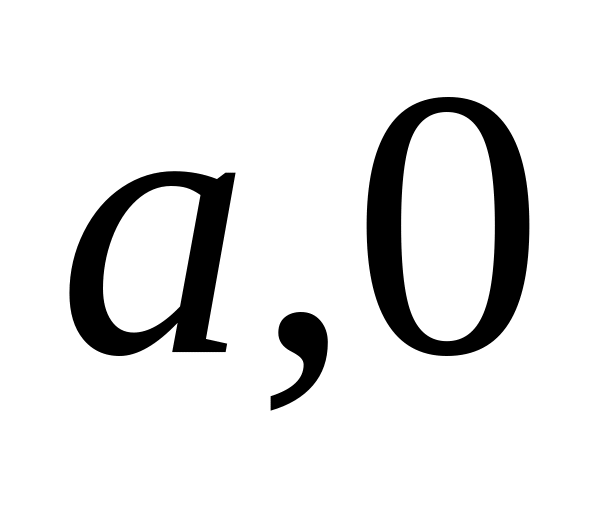 ).
).Якщо в загальному рівнянні прямої С=0, то пряма проходить через вісь ординат.
Нормаллю до прямої в просторі називається вектор, колінеарний цій прямій.
Кут між прямими на площині обчислюють за відомими направляючими векторами.
Дві прямі паралельні, якщо відповідні коефіцієнти пропорційні.
Кут між мимобіжними прямими обчислити не можна. (7б)
Задачі:
Скласти рівняння медіани, і висоти, опущені з вершини В(1,3,2), якщо А(1,1,4) і С(4,6,-1). (6б)
Скласти загальне рівняння прямої, яка проходить через точки А(6,5,4) В(5,0,2). (4б)
Зобразіть площину, яка проходить через три точки А(5,6,7), В(-6,-2,0) і С(1,-1,2), записавши рівняння в відрізках на осях. (5б)
Обчисліть відстань від точки М(-2,-1,-1) до площини
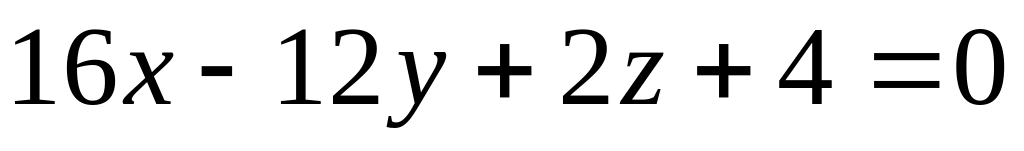 (3б)
(3б)
Варіант №4
Через три точки на площині проходить єдина пряма.
Із канонічного рівняння координати направляючого вектора (А,В).
Якщо кут між нормалями прямої від‘ємний, то кут між прямими тупий.
Пряму в просторі можна задати як перетин двох площин.
Направляючий вектор прямої у просторі співпадає з нормалями до площин, які при перетині утворюють пряму.
Якщо в загальному рівнянню площини А=0, то площина перпендикулярна вісі абсцис.
Для того щоб прямі на площині співпадали, необхідно і достатньо, щоб коефіцієнти із загального рівняння співпадали. (7б)
Задачі:
Скласти рівняння медіани, бісектриси і висоти, опущені з вершини В(3,2), якщо А(9,-4) і С(5,7). (6б)
Скласти загальне рівняння прямої, яка проходить через точки А(2,2,1) В(-4,6,-8). (4б)
Зобразіть площину, яка проходить через три точки А(1,-1,4), В(0,1,7) і С(2,8,-1), записавши рівняння в відрізках на осях. (5б)
Обчисліть відстань від точки М(-3,-6,7) до площини
 (3б)
(3б)
Модуль 3 Криві другого порядку
Стислий конспект
|
Означення |
Вісі, фокуси |
Ексцентриситет, директриса |
Малюнок |
Еліпс |
Еліпсом
називається геометричне місце точок
площини, для кожної з яких сума відстаней
від заданої точки до двох фіксованих
точок площини (фокусів)
є величина постійна (яка дорівнює
|
Відстань
між фокусами
Фокуси лежать на великій осі
|
Для
еліпса
Директрисами називається прямі паралельні малі осі і мають рівняння
|
|
Коло |
Коло – це геометричне місце точок, рівновіддалених від однієї, яку називають центром. Канонічне
рівняння кола з центром в точці О(0,0)
і радіусом
має вид
|
Фокуси співпадають з центром, а піввісі з радіусом |
Для
кола
Директрис немає.
|
|
Гіпербола |
Гіперболою називається геометричне місце точок площини, для кожної з яких модуль різниці відстаней від заданої точки до двох фіксованих точок площини (фокусів) є величина постійна (яка дорівнює ).
|
- дійсна вісь, - дійсна піввісь, - уявна вісь, - уявна піввісь. Відстань між фокусами . Фокуси лежать на дійсній осі
|
- ексцентриситет – це відношення значення фокуса до дійсної півосі
Для
гіперболи
Директрисами називається прямі паралельні уявній осі і мають рівняння . |
|
Спряжена гіпербола |
|
- уявна вісь, - уявна піввісь, - дійсна вісь, - дійсна піввісь. Відстань між фокусами . Фокуси лежать на дійсній осі
|
Директрисами називається прямі паралельні уявній осі і мають рівняння
|
|
Парабола |
Парабола
– це множина точок площини, для кожної
з яких відстань до деякої точки
Число
|
Пряма, перпендикулярна директрисі і проходить через фокус, називається віссю параболи. Точка перетину параболи з її віссю називається вершиною параболи
|
Для пароболи е=1 Директрисою називається пряма перпендикулярна осі симетрії параболи.
рівняння
директриси
|
|
Спряжена парабола |
|
Фокус
лежить на осі симетрії параболи і має
координати
|
Для пароболи е=1 рівняння директриси (перпендикулярно осі Оy)
|
|
Лінії другого порядку (ЛДП) в полярній системі координат.
Нехай існує довільна крива. Розглянемо її довільний фокус та відповідну йому директрису. Полярну систему координат виберемо так, що полюс О збігається з фокусом, а полярна вісь направлена вздовж осі симетрії лінії в бік, протилежний директриси.
![]() -
рівняння
ЛДП в полярній системі координат.
-
рівняння
ЛДП в полярній системі координат.
При
- еліпс,
![]() - гіпербола,
- гіпербола,
![]() - парабола,
- коло. Фокальний параметр р для параболи
визначається безпосередньо з рівняння
.
Для еліпса і гіперболи фокальний параметр
являється ординатою точки кривої,
абсциса якої дорівнює абсцисі відповідного
фокуса в ПДСК, тобто
- парабола,
- коло. Фокальний параметр р для параболи
визначається безпосередньо з рівняння
.
Для еліпса і гіперболи фокальний параметр
являється ординатою точки кривої,
абсциса якої дорівнює абсцисі відповідного
фокуса в ПДСК, тобто![]()
Приклади розв’язання задач
Задача
1: записати рівняння еліпса
![]() в полярних координатах. Для цього
визначимо
в полярних координатах. Для цього
визначимо
![]() ,
,
![]() .
Для заданого еліпса
.
Для заданого еліпса
![]() .
Можна записати рівняння еліпса в полярних
координатах
.
Можна записати рівняння еліпса в полярних
координатах
![]() .
.
Практичні завдання
Практичне заняття №15
Тема: Парабола.
І. Завдання корекції знань:
1. Скласти рівняння параболи, вершина якої знаходится на початку координат, знаючи, що:
1) парабола розташована в правій півплощині, симетрично відносно вісі Ох, і її параметр
р = 3;
2) парабола розташована в лівій півплощині, симетрично відносно вісі Ох, і її параметр
р = 0,5;
3)
парабола розташована
в верхній півплощині,
симетрично відносно
вісі
Оу,
і
її
параметр p
=
![]() ;
;
4) парабола розташована в нижній півплощині, симетрично відносно вісі Оу, і її параметр р =3.
2. Визначити величину параметру і розташування відносно координатних вісей наступних парабол:
1) у2 = 6х; 2) х2 = 5у; 3) у2 = — 4х; 4) х2 = — у.
3. Скласти рівняння параболи, вершина якої знаходиться на початку координат, знаючи, що:
1) парабола симетрично розташована відносно осі Ох і проходить через точку А (9; 6);
2) парабола симетрично розташована відносно осі Ох і проходить через точку В(—1; 3);
3) парабола симетрично розташована відносно осі Оу і проходить через точку С(1; 1);
4 парабола симетрично розташована відносно осі Оу і проходить через точку D (4; — 8).
4. Скласти рівняння параболи, якщо дані її фокус F(2; —1) та директриса х — у — 1 = 0.
5. Визначити точку перетину прямої х + у— 3 = 0, і параболи х2 = 4у.
ІІ. Завдання для самостійного розв’язання
1. Встановити, що кожне з наступних рівнянь визначає параболу, і знайти координати їївершини А, величину параметра р і рівняння директриси:
1) у2 = 4х — 8, 2) у2 = 4 — 6х,
3) х2 = 6у + 2, 4) х2 = 2— у.
2. Скласти рівняння параболи, якщо дано її фокус F(4; 3) і директриса у + 1 = 0.
3. Дано вершина параболи А(—2; —1) і рівняння її директриси х + 2у — 1 = 0.
Скласти рівняння цієї параболи.
Практичне заняття № 16
Тема: коло
І. Завдання корекції знань:
1.Скласти рівняння кола в кожному з наступних випадків:
1) центр кола співпадає з початком координат і її радіус R = 3;
2) центр кола співпадає з точкою С(2; — 3) і її радіус R = 7;
3) коло проходить через початок координат і її центр співпадає з точкою С (6; — 8);
4) коло проходить через точку А(2; 6) і її центр співпадає з точкой С(—1; 2);
5) точки А(3; 2) і В(—1; 6) є кінцями однієї з діаметрів кола;
6) центр кола співпадає з початком координат і пряма 3х — 4у + 20 = 0 є дотичною ло кола;
7) центр кола співпадає з точкою С(1; —1) і пяряма 5х—12у + 9 = 0 є дотичною до кола
8) коло проходить через точки А(3; 1) і В(—1; 3), а її центр лежить на прямій 3х — у — 2=0;
9) коло проходить через три точки: А(1; 1), B(1; — 1) і С(2; 0);
10) коло проходить через три точки: M1(— 1; 5), М2(— 2; — 2) і M3 (5; 5).
2. Точка С(3; — 1) є центром кола, відтинаючою на прямій 2х — 5у + 18 = 0
хорду, довжина якої дорівнює 6. Скласти рівняння цього кола.
3.
Написати
рівняння кіл радіуса
R
=![]() ,
дотичних
прямій
х
— 2у
— 1=0
в точці
М1
(3;
1).
,
дотичних
прямій
х
— 2у
— 1=0
в точці
М1
(3;
1).
4. Скласти рівняння кіл, дотичних двох паралельних прямих: 2х + у — 5 = 0,
2х + у +15 = 0, при чому однеї з них — в точці А(2; 1).
5. Скласти рівняння кіл, які проходять через точку А(1; 0) і дотикаються двох паралельных прямих: 2х + у + 2 = 0, 2х + у — 18 = 0.
ІІ. Завдання для самостійного розв’язання
1. Скласти рівняння кола, яке, маючи центр на прямій дотикається до прямих
2х + у = 0, 4х — 3у+10 = 0, 4х — 3у — 30 = 0.
2. Скласти рівняння кіл, дотичних двом пересічним прямим 7х – у – 5 = 0, х + у + 13 = 0, при чому однієї з них – в точці М1 (1; 2).
3. Скласти рівняння кіл, які проходять через початок координат і дотичні до двох пересічних прямих: х + 2у – 9 = 0, 2х – у + 2 = 0.
Практичне заняття № 17
Тема: Еліпс
І. Завдання корекції знань:
1. Скласти рівняння еліпса, фокуси якого лежать на вісі абсцис, симетрично відносно початку координат, знаючи, окрім того, що:
1) його піввісі дорівнюють 5 і 2;
2) його велика вісь дорівнює 10, а відстань між фокусами 2с = 8;
3) його мала вісь дорівнює 24, а відстань між фокусами 2с =10;
4)
відстань
сіж його
фокусами 2с
= 6 і
ексцентриситет
![]() ;
;
5) його велика вісь дорівнює 20, а ексцентриситет ;
6)
його
мала
вісь
дорівнює
10, а ексцентриситет
![]() ;
;
7) відстань між його директрисами дорівнює 5 і відстань між фокусами 2с = 4;
8) його велика вісь дорівнює 8, а відстань між директрисами дорівнює 16;
9) його мала вісь дорівнює 6, а відстань між директрисами дорівнює 13;
10)
відстань
між його
директрисами дорівнює
32 і
![]() .
.
2. Скласти рівняння еліпса, фокуси якого лежать на вісі ординат, симетрично відносно початку координат, знаючи, окрім того, що:
1) його піввісі дорівнюють відповідно 7 і 2;
2) його велика вісь дорівнює 10, а відстань між фокусами 2с = 8;
3)
відстань
між його
фокусами 2с = 24 і
ексцентриситет
![]()
4) його мала вісь дорівнює16, а ексцентриситет
5)
відстань
між його
фокусами 2с = 6 і
відстань між директрисами
дорівнює
16![]()
6)
відстань
між його
директрисами дорівнює
![]() і
ексцентриситет
і
ексцентриситет
![]()
3. Визначити піввісі кожного з наступних еліпсів:
1)
![]() ;
2)
;
2)
![]() ;
3)х2
+ 25у2
= 25;
;
3)х2
+ 25у2
= 25;
4) х2 + 5y2 = 15; 5) 4х2 + 9у2 = 25; 6) 9х2 + 25у2 = 1;
7) х2 + 4у2 = 1; 8) 16х2 + у2 = 16; 9) 25х2 + 9у2 = 1;
10) 9х2 + у2 = 1.
5. Дано еліпс 9х2 + 25у2 = 225. Знайти: 1) його піввісі; 2) фокуси; 3) ексцентриситет; 4) рівняння директрис.
6. Знайти точки перетину прямої х + 2у — 7 = 0 і еліпса х2 + 4у2 = 25.
7.
З
точки С(10; —8) проведені
дотичні
до
еліпса
![]()
Скласти рівняння хорди, що з’єднає точки дотику.
8. Еліпс який проходить через точку А (4; —1) і дотикається до прямої прямой
х + 4у—10 = 0. Скласти рівняння цього еліпса при умові, що йог вісі співпадають з осями координат.
ІІ. Завдання для самостійного розв’язання
1. Дано еліпс 9х2 + 5у2 = 45. Знайти: 1) його піввісі; 2) фокуси; 3) ексцентриситет; 4) рівняння директрис.
2.
Ексцентриситет
еліпса
![]() , фокальний
радіус
точки М
еліпса
дорівнює
10. Обчислити
відстань від точки
М
до
односторонньої
з
цим
фокусом директриси.
, фокальний
радіус
точки М
еліпса
дорівнює
10. Обчислити
відстань від точки
М
до
односторонньої
з
цим
фокусом директриси.
3.
Визначити
точки еліпса
![]() ,
відстань
яких до правого фокуса дорівнює
14.
,
відстань
яких до правого фокуса дорівнює
14.
Практичне заняття №18
Тема: Гіпербола.
І. Завдання корекції знань:
1. Скласти рівняння гіперболи, фокуси якої розташовані на осі абсцис, симетрично відносно початку координат, знаючи, окрім того, що:
1) її вісі 2а = 10 і 2b = 8;
2) відстань між фокусами 2с =10 і вісь 2b = 8;
3)
відстань
між
фокусами 2с
= 6 і
ексцентриситет
ε =![]() ;
;
4)
вісь
2a
= 16 і
ексцентриситет
ε =![]() ;
;
5)
рівняння
асимптот
y
= ±
![]() і відстань між фокусами
2с
— 20;
і відстань між фокусами
2с
— 20;
6) відстань між директрисами дорівнює 22 — і відстань між фокусами 2с = 26;
7)
відстань
між
директрисами
дорівнює
![]() і
вісь
2b = 6;
і
вісь
2b = 6;
8)
відстань
між
директрисами дорівнює
![]() і
ексцентриситет
ε =
;
і
ексцентриситет
ε =
;
9)
рівняння
асимптот у
= ±![]() і
відстань
між
директрисами дорівнює
12
і
відстань
між
директрисами дорівнює
12![]()
2. Скласти рівняння гіперболи, фокуси якої розташовані на осі ординат, симетрично відносно початку координат, знаючи, окрім того, що:
1) її піввісі а = 6, b = 18 (літерою «а» ми позначаємо піввісь гіперболи, розташовану на осі абсцис);
2)
відстань
між фокусами
2с
=10 і
ексцентриситет
ε
=![]() ;
;
3)
рівняння
асимптот
у
= ±![]() і
відстань
між
вершинами
дорівнює
48;
і
відстань
між
вершинами
дорівнює
48;
4)
відстань
між
директрисами дорівнює
![]() і
ексцентриситет
ε =
і
ексцентриситет
ε =![]() ;
;
5)
рівняння
асимптот у
= ±
і
відстань
між
директрисами дорівнює
![]() .
.
3. Дано гіпербола 16х2 — 9у2 = —144. Знайти: 1) піввісі а і b; 2) фокуси;
3) ексцентриситет; 4) рівняння асимптот; 5) рівняння директрис.
4. Скласти рівняння гіперболи, знаючи, що:
1) відстань між її вершинами дорівнює 24 і фокуси F1(— 10; 2), F2(16; 2);
2) фокуси F1(3; 4), F2(— 3; — 4), відстань між директрисами дорівнює 3,6;
3) кут між асимптотами дорівнює 90° і фокуси F1 (4; — 4), F2(—2; 2)
5.
Знайти
точки перетину
прямої
2х—у—10=0
і
гіперболи
-![]()
6.
Провести дотичні
до
гіперболи
![]() .
паралельно прямої
2х
+ 4у —5 = 0
.
паралельно прямої
2х
+ 4у —5 = 0
і обчислити відстань d між ними.
ІІ. Завдання для самостійного розв’язання
1.
Скласти рівняння гіперболи, якщо відомі
її ексцентриситет ε
=
![]() ,
фокус F
(5;
0) і рівняння відповідної директриси
5х — 16 = 0.
,
фокус F
(5;
0) і рівняння відповідної директриси
5х — 16 = 0.
2. Скласти рівняння гіперболи, фокуси якої лежать на осі абсцис симетрично відносно початку координат, якщо дано:
3)
точка M1(![]() ;
—1) гіперболи
і
рівняння
асимптот y =
;
—1) гіперболи
і
рівняння
асимптот y = ![]() ;
;
4)
точка M1(—3;
![]() )
гіперболи
і
рівняння
директрис y =
)
гіперболи
і
рівняння
директрис y = ![]() ;
;
5)
рівняння
асимптот
у
=
і
рівняння
директрис x = ![]() ;
;
Практичне заняття №19
Тема: Полярні рівняння кривих другого порядку.
І. Завдання корекції знань:
1.
Дано рівняння гіперболи
![]() =
1. Скласти полярне рівняння її лівої
гілки, вважаючи, що направлення полярної
осі співпадає з позитивним направленням
осі абсцис, а полюс знаходиться:
=
1. Скласти полярне рівняння її лівої
гілки, вважаючи, що направлення полярної
осі співпадає з позитивним направленням
осі абсцис, а полюс знаходиться:
1) в левому фокусі гіперболи; 2) в правому фокусі.
2. Дано рівняння параболи у2 = 6х. Скласти полярне рівняння, вважаючи, що направлення полярної осі співпадає з позитивним направленням осі абсцис, а полюс знаходиться в фокусі параболы.
3. Определить, какие линии даны следующими уравнениями в полярных координатах:
1)
 ,
2)
,
2)
 , 3)
, 3)
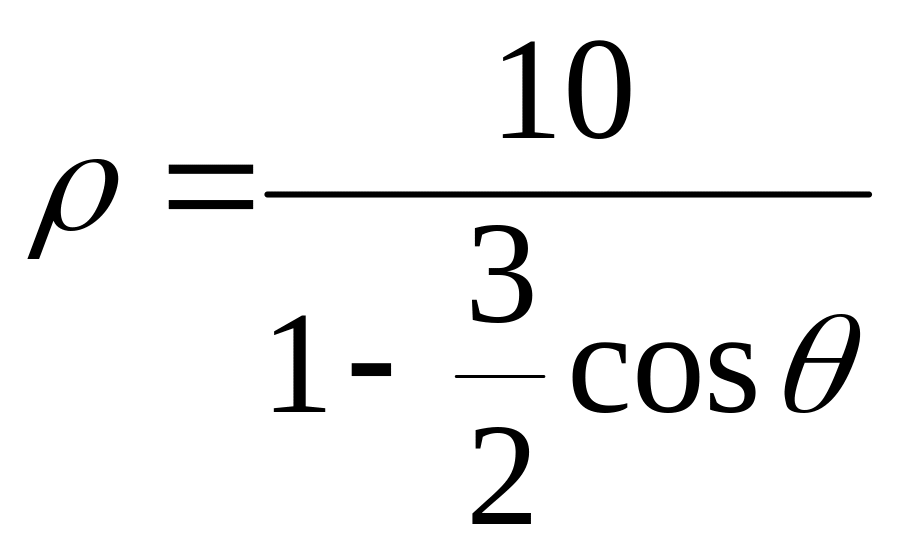 ,
,
4)
![]() ,
5)
,
5)
![]() , 6)
, 6)
![]() ,
,
4.
Встановити,
що
рівняння
![]() ,
визначає
еліпс
і
знайти
його
піввісі.
,
визначає
еліпс
і
знайти
його
піввісі.
5.
Встановити,
що
рівняння![]() визначає
праву гілку
гіперболи
і
знайти
її
піввісі.
визначає
праву гілку
гіперболи
і
знайти
її
піввісі.
ІІ. Завдання для самостійного розв’язання
1. Встановіть, що рівняння визначає праву гілку гіперболи і знайти її піввісі.
2.
Встановіть,
що рівняння![]() визначає
еліпс і
скласти
полярні рівняння
його
директрис.
визначає
еліпс і
скласти
полярні рівняння
його
директрис.
Практичне заняття №20
Тема: Загальне рівняння ліній другого порядку.
І. Завдання корекції знань:
Звести загальні рівняння кривих до канонічного виду
1) 3х2 — 4ху — 2у2 + 3х — 12у — 7 = 0;
2) 4х2 + 5ху + 3y2 — х + 9у — 12 = 0;
3) 4х2 — 4ху +y2 — 6х + 8у + 13 = 0;
4) 4х2 — 4ху + y2 — 12х + 6у — 11 = 0;
5) х2 — 2ху + 4у2 + 5х —7у+12=0;
6) х2 — 2ху + у2 — 6х + 6у — 3 = 0;
7) 4х2 — 20ху + 25у2 — 14х + 2у — 15 = 0;
8) 4х2 — 6ху — 9у2 + 3х — 7у + 12 = 0.
9) 3х2 + 5ху +y2 — 8х — 11у — 7 = 0;
10) 5х2 + 4ху + 2y2 + 20х+ 20у — 18 = 0;
11) 9х2 — 4ху — 7y2 — 12 = 0;
12) 2х2 — 6ху + 5у2 + 22х — 36у + 11 = 0.
13) 32х2 + 52ху — 7у2 + 180 = 0;
14) 5х2 — 6ху + 5у2 — 32 = 0;
15) 17х2 — 12ху + 8у2 = 0;
16) 5х2 + 24ху — 5у2 = 0;
17) 5х2 — 6ху + 5у2 + 8 = 0.
ІІ. Завдання для самостійного розв’язання
Звести загальні рівняння кривих до канонічного виду
1) 4х2 + 9y2 — 40х+ 36у + 100 = 0;
2) 9х2—16у2 —54х — 64у — 127 = 0;
3) 9х2 + 4у2 + 18х — 8у + 49 = 0;
4) 4х2 — у2 + 8х — 2у + 3 = 0;
5) 2х2 + 3y2 + 8х — 6у + 11=0.
Практичне заняття №21
Тема: Дослідження ліній другого порядку
І. Завдання корекції знань:
Провести дослідження кривих, записати їх канонічне рівняння
1) 2х2+10ху+12у2 —7х + 18у —15 = 0;
2) 3х2 — 8ху + 7у2 + 8х — 15у + 20 = 0;
3) 25х2 — 20ху + 4у2 — 12х + 20у —17 = 0;
4) 5х2 + 14ху + 11у2 + 12х — 7у + 19 = 0;
5) х2 — 4ху + 4у2 + 7х — 12 = 0;
6) 3х2 — 2ху — 3у3 + 12у — 15 = 0.
7) 3х2+10ху + 3у2 —2х—14у—13 = 0;
8) 25х2 — 14ху + 25y2 + 64х — 64у — 224 = 0;
9) 4ху + 3у2 + 16х + 12у — 36 = 0;
10) 7х2 + 6ху — у2 + 28х + 12у + 28 = 0;
11) 19x2 + 6xy + 11y2 + 38x + 6y + 29 = 0;
12) 5х2 — 2ху + 5у2 — 4х + 20у + 20 = 0.
13) 14х2 + 24ху + 21у2 — 4х+18у—139 = 0;
14) 11х2 —20ху —4у2 —20х—8у+1=0;
15) 7х2 + 60ху + 32у2 — 14х — 60у + 7 = 0;
16) 50х2 — 8ху + 35у2 + 100х — 8у + 67 = 0;
17) 41х2 + 24ху + 34у2 + 34х — 112у + 129 = 0;
18) 29х2 —24ху+36у2 + 82х—96у —91=0;
19) 4х2 + 24ху + 11у2 + 64х + 42у + 51 = 0;
20) 41х2 + 24ху + 9у2 + 24х+18у —36 = 0.
21) 8х2—12ху+17у2+16х—12у + 3 = 0;
ІІ. Завдання для самостійного розв’язання
Провести дослідження кривих, записати їх канонічне рівняння
1) 17х2 —18ху —7у2 + 34х—18у + 7 = 0;
2) 2х2 + 3ху — 2у2 + 5х + 10у = 0;
3) 6х2 —6ху + 9у2 —4х+18у+14 = 0;
4) 5х2 —2ху + 5у2 —4х + 20у + 20 = 0.
Практичне заняття №22
Тема: Перетворення рівнянь ліній другого порядку за допомогою інваріантів.
І. Завдання корекції знань:
Використовуючи інваріанти, звести рівняння кривих до канонічного виду. Встановити вид кривої.
1) 4х2 + 24ху + 11у2 + 64х + 42у + 51=0;
2) 12х2 + 26ху + 12у2 — 52х — 48у + 73 = 0;
3) 3х2 + 4ху — 12х + 16 = 0;
4) х2 — 6ху — 7у2 + 10х — 30у + 23 = 0.
5) 3х2 + 4ху + у2 — 2х — 1=0;
6) х2 — 6ху + 8у2 — 4у — 4 = 0;
7) х2 — 4ху + 3у2 = 0;
8) х2 + 4ху + 3у2 — 6х — 12у + 9 = 0.
9) х2 + 4ху + 4у2 + 4х+у—15 = 0;
10) 9х2 —6ху+у2 —х + 2у—14 = 0;
ІІ. Завдання для самостійного розв’язання
Використовуючи інваріанти, звести рівняння кривих до канонічного виду. Встановити вид кривої.
1) 25х2 — 20ху + 4у2 + 3х —у +11=0;
2) 16х2+16ху + 4у2 — 5х + 7у = 0;
3) 9х2 — 42ху + 49у2 + 3х — 2у — 24 = 0.
Приклади модульного завдання
Варіант №1.
Крива, яка має один фокус, називається колом.
Вісь, на якій розташовані фокуси гіперболи, називається явною.
Парабола, фокус якої
 симетрична
осі ординат.
симетрична
осі ординат.Директриси еліпса можуть перетинати його. (4б)
Задачі:
Скласти канонічне рівняння еліпса, який проходить через точку
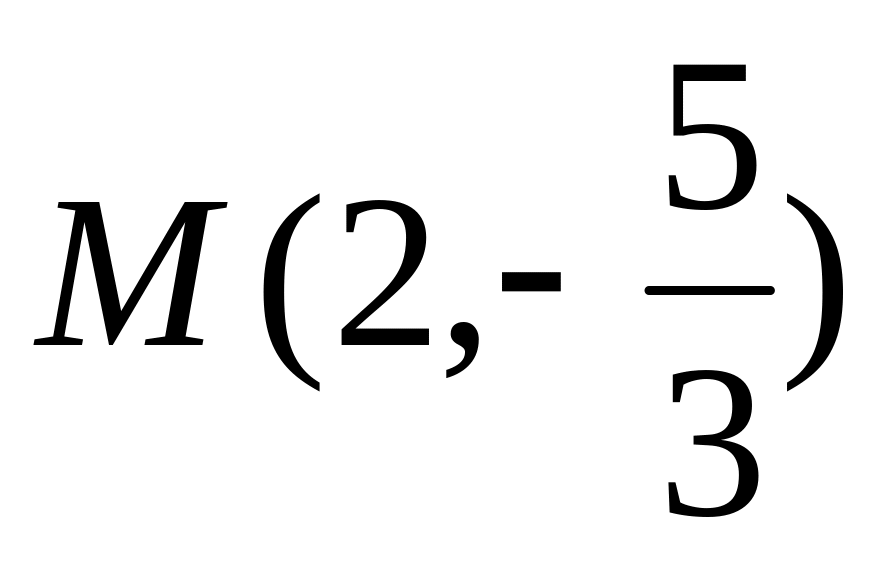 і ексцентриситет
і ексцентриситет
 .
Зобразити. (3б)
.
Зобразити. (3б)Знайти фокус параболи, симетричної відносно вісі абсцис з директрисою
 .
Зобразити. (3б)
.
Зобразити. (3б)Задана гіпербола
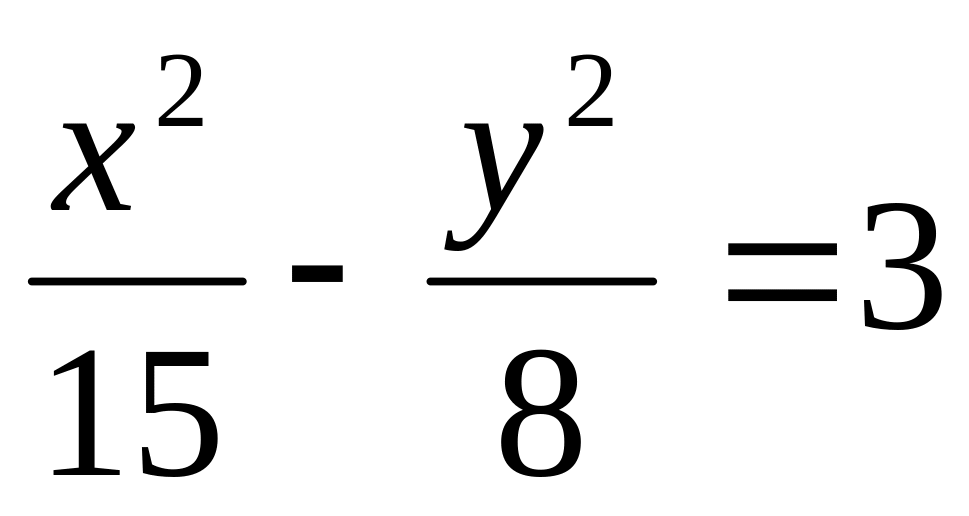 .
Знайти її піввісі, фокуси, ексцентриситет,
директриси, асимптоти та її зобразити.
(4б)
.
Знайти її піввісі, фокуси, ексцентриситет,
директриси, асимптоти та її зобразити.
(4б)Скласти рівняння кола, яке проходить через три точки А(2,2), В(2,-2), С(4,0). (6б)
Варіант №2.
Крива, яка має один фокус, називається еліпсом.
Вісь, на якій розташовані фокуси еліпса, називається великою.
Парабола, фокус якої
 симетрична
осі абсцис.
симетрична
осі абсцис.Директриси параболи можуть перетинати його.
Задачі:
Скласти канонічне рівняння еліпса, який проходить через точку
 і відстань між директрисами 10. Зобразити.
і відстань між директрисами 10. Зобразити.Знайти фокус параболи, симетричної відносно вісі ординат з директрисою
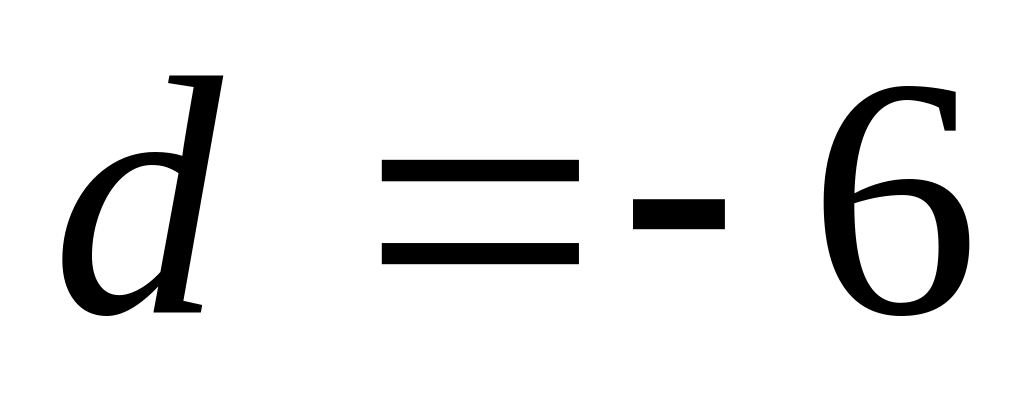 .
Зобразити.
.
Зобразити.Задана гіпербола
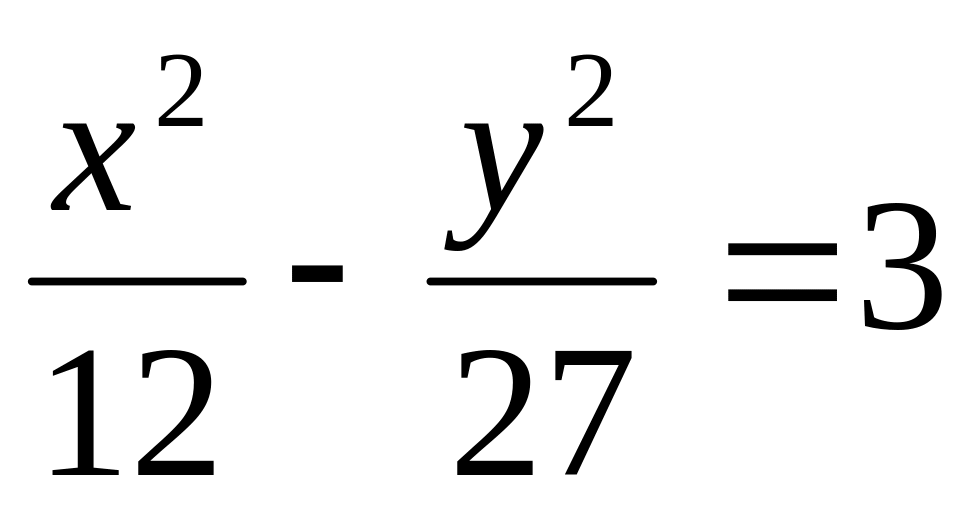 .
Знайти її піввісі, фокуси, ексцентриситет,
директриси, асимптоти та її зобразити
.
Знайти її піввісі, фокуси, ексцентриситет,
директриси, асимптоти та її зобразити
Скласти рівняння кола, центр якого співпадає з точкою С(1,-2) і пряма
 являється
дотичною до кола.
являється
дотичною до кола.
Варіант №3.
Крива, яка має один фокус, називається гіперболою.
Вісь, на якій розташований фокус параболи, називається дійсною.
Парабола, фокус якої
 симетрична
осі ординат.
симетрична
осі ординат.Директриси еліпса паралельні малій вісі.
Задачі:
Скласти канонічне рівняння еліпса, відстань одного з фокусів до кінців великої вісі дорівнюють 7 і 1.
Знайти фокус параболи, симетричної відносно вісі абсцис з директрисою
 .
.Встановити тип кривої, використовуючи інваріанти
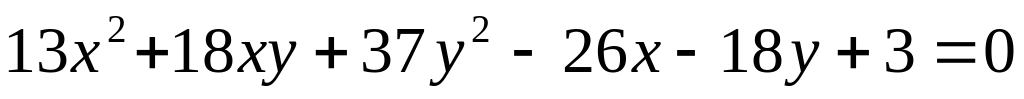 .
.Звести рівняння кривої до канонічного виду, вказуючи вид перетворення
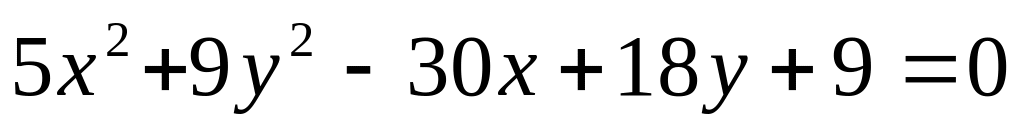 .
.
Варіант №4.
Асимптоти гіперболи завжди співпадають з її осями.
Вісь, на якій розташовані фокуси гіперболи, називається дійсною.
Парабола, з директрисою 3, симетрична осі ординат має фокус
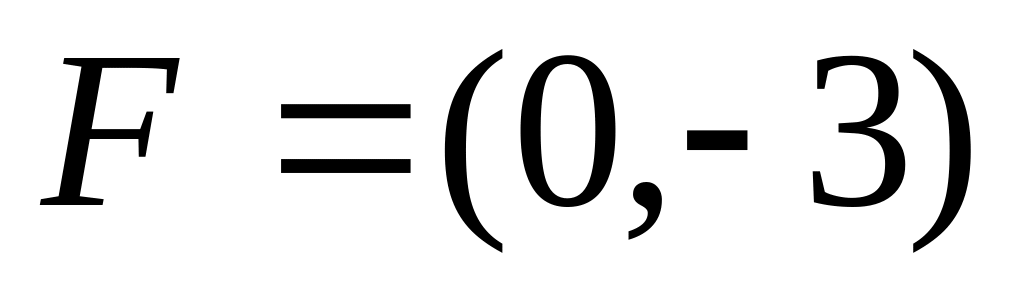 .
.Директриси еліпса паралельні великій вісі.
Задачі:
Скласти канонічне рівняння еліпса, директриси якого
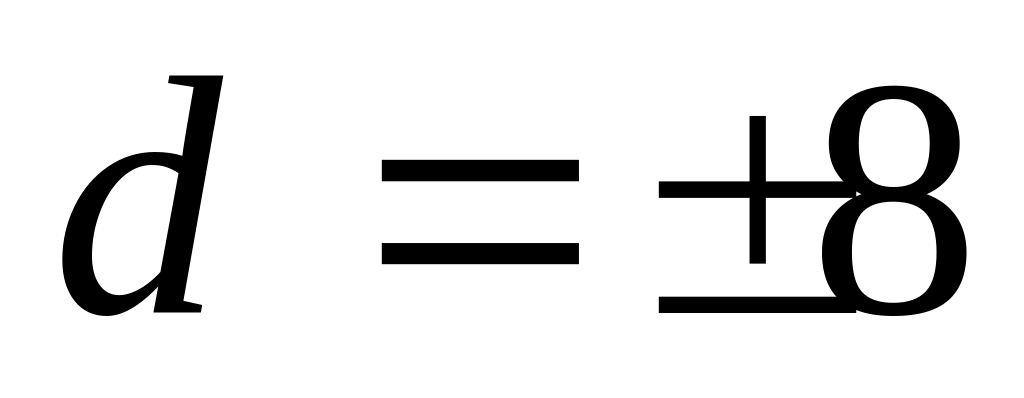 і мала вісь 8.
і мала вісь 8.Знайти фокус параболи, симетричної відносно вісі ординат з директрисою
 .
.Встановити тип кривої, використовуючи інваріанти
 .
.Звести рівняння кривої до канонічного виду, вказуючи вид перетворення
 .
.
Модуль 4. «Поверхні другого порядку.»
Стислий конспект
Циліндричні поверхні (ЦП).

 Фокус
лежить на осі симетрії параболи і має
координати
Фокус
лежить на осі симетрії параболи і має
координати