Орієнтовані площини і простори.

Двійка векторів – права, якщо поворот від першого вектора до другого здійснюється проти ходу годинникової стрілки, якщо – за годинниковою стрілкою, то двійка векторів – ліва.

Ліва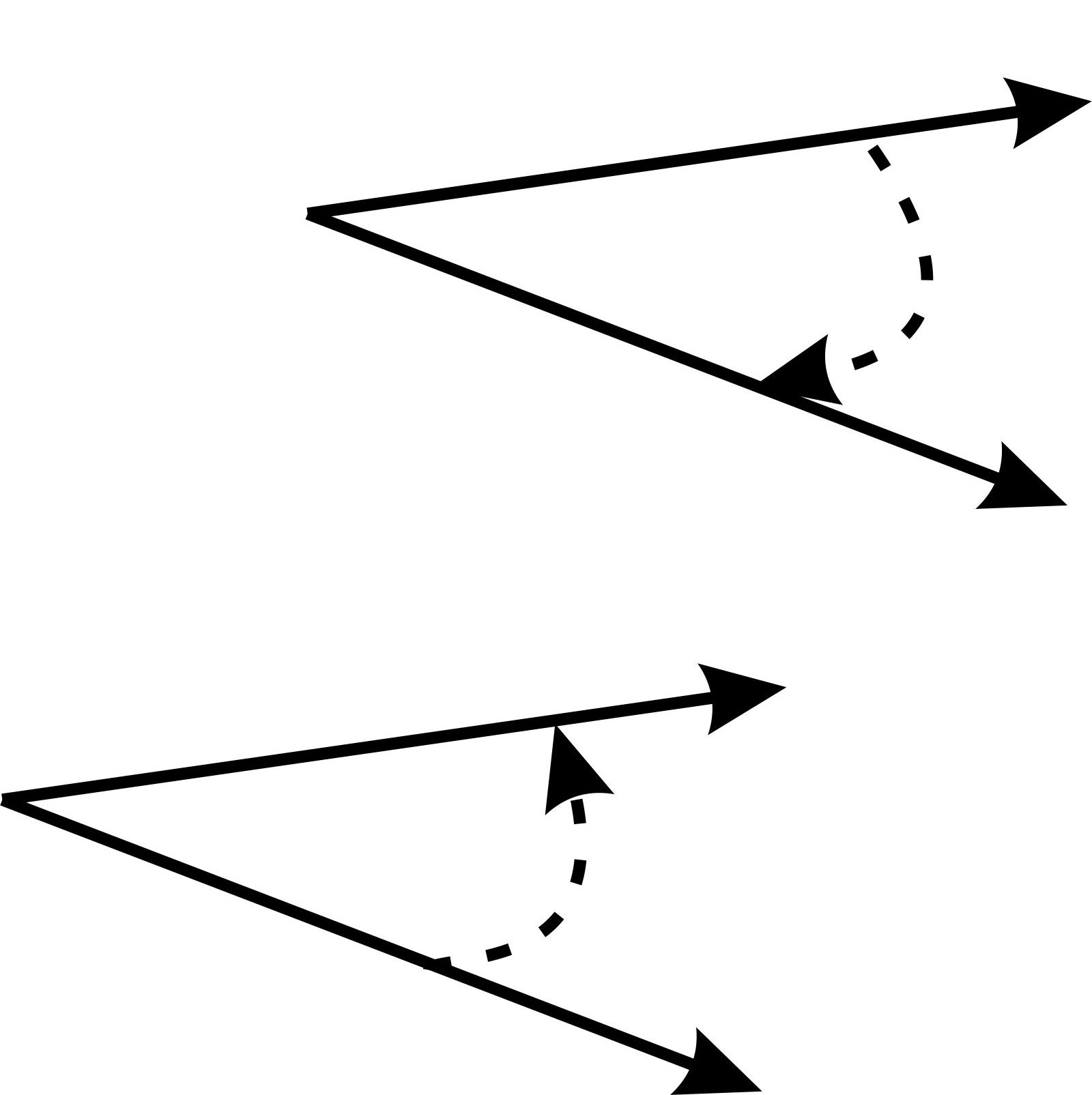

Права

Трійка векторів – права, якщо глядячи з кінця третього вектора, поворот від першого вектора до другого здійснюється проти ходу годинникової стрілки, і ліва, якщо – за ходом годинникової стрілки.

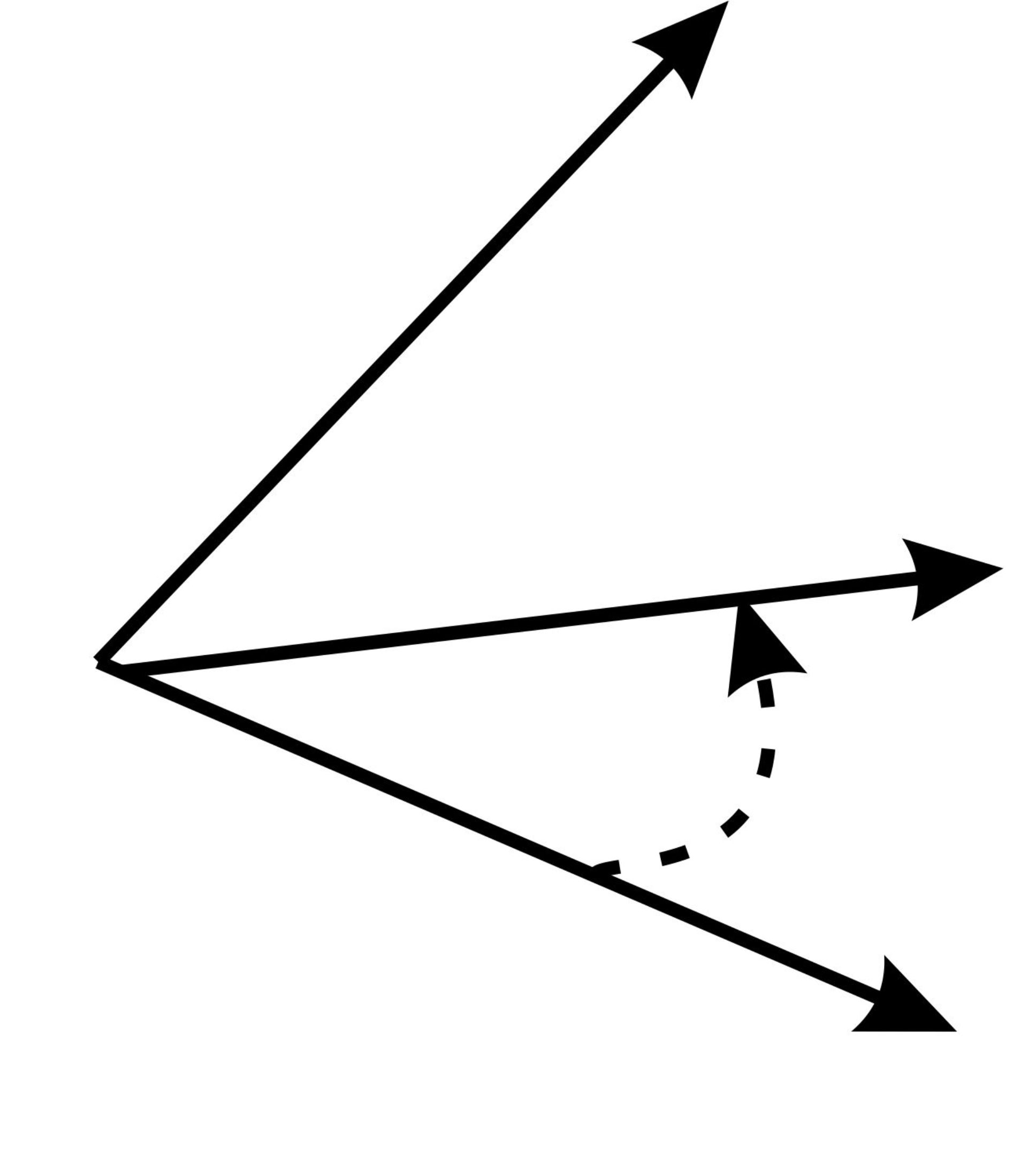
Якщо в орієнтованій трійці змінити місцями два вектора, то трійка змінить орієнтацію на протилежну.

Приклади розв’язання типових задач

Задача 1. Показати що вектори колінеарні.

Розв’язок: Дійсно, вектори колінеарні, якщо відповідні їх координати пропорційні .

Перевіримо , коефіцієнт пропорційності , отже і колінеарні.

Відповідь:

Задача 2. Чи являються вектори ; ; лінійно залежними?

Розв’язок 1: За означенням: вектори лінійно не залежні, якщо утворюють лінійну комбінацію. (_*) при .

Підставимо в рівність (_*) лінійні комбінації векторів .

;Розкриваємо дужки і згруповуємо додатки, які містять вектори , потім , а потім

(_**).

бо вектори утворюють базис (являються лінійно не залежні) простору 3, то лінійна комбінація (_**) нульова і тривіальна, а значить всі коефіцієнти при векторах дорівнюють нулю. Отримуємо систему рівнянь:

, яку можна розв’язати методом Крамера

;

Тоді: ; ; ;

Отже за формулами Крамера ; ; в лінійній комбінації (_*).

Коефіцієнти , значить, трійка векторів являються лінійно незалежна.

Цю задачу можна розв’язати іншим способом, враховуючи властивості лінійного добутку векторів.

Розв’язок 2. Відомо , що трійка векторів - компланарна (вектори лежать в одній площинні) тоді і тільки тоді , коли їх мішаний добуток дорівнює нулю . Якщо мішаний добуток відмінний від нуля, то вектори не компланарні і не лежать в одній площині, тобто являються ЛНЗ.

порівняти його з нулем.

Маємо вектори не компланарні, значить лінійно не залежні.

Відповідь: вектори являються ЛНЗ.

Задача 3. Представити вектор в виді лінійної комбінації векторів ,

, .

Розв’язок: Якщо вектори - ЛНЗ, тобто утворюють базис тривимірного простору, тоді за

теоремою: кожний вектор простору єдиним чином можна представити в виді лінійної комбінації базисних векторів.

(_*).

Якщо кожний вектор представити в виді:

, , , , то вираз (_*), після алгоритмічних перетворень можна записати в виді системи рівнянь:

Розв’яжемо її методом Крамера:

Тоді: ; Отже: ; ; ;

Отже вектор має вид ;

Відповідь:

Задача 4. Задано вершини піраміди , , ,

1. Обчислити площу основи.

2. Обчислити периметр (основи піраміди).

3. Обчислити площу основу.

4. Знайти кути при основі.

5. Знайти об’єм піраміди.

6. Довжину висоти піраміди, опущену з вершини на основу.

Розв’язок:

1. Зобразимо в ПДСК піраміду. Для цього побудуємо ПДСК в тривимірному просторі (кількість координат точок – три). Нанесемо на неї кожну точку окремо, з`єднаємо точки отримаємо піраміду

2. Обчислити периметр .

Нагадуємо периметром фігури називається сума довжин всіх сторін. В даній задачі

утворюють три сторони , , . Так як вершинами задані координати, то використовують наступну формулу .

Спочатку використовуємо координати векторів за правилами: від координату кінця віднімаємо координати початку.

;

;

;

Їх довжини дорівнюють відповідно:

;

Аналогічно:

і

Отже, і наближено, (од.)

3. Обчислити площу побудовано на векторах , тоді для відшукання площі використовуємо формулу .

Координати векторів , були знайдені в попередній задачі.

Спочатку запишемо та обчислимо векторний добуток за формулою , а саме ;

Тепер залишилося обчислити довжину останнього вектора. Можна показати , що (кв. од.)

Площа основи складає (кв. од.) або наближено 20.72 (кв. од.)

4. Знайти кути при основі. В основі піраміди лежить . Із вершини А виходять два вектора

і , отже для знаходження кута А скористуємося формулою

Скалярний добуток векторів

Тоді , тоді

Із вершини В виходять два вектора :

Тоді ;Координати ; ;

Їх скалярний добуток .

, значить (за табл.. Брадіса)

Кут С знайдемо із рівності

5. Об'єм піраміди обчислюється за формулою . Основою піраміди є ,

піраміда побудувала на векторах , , . Знайдемо їх координати

;

;

;

Обчислимо мішаний добуток , тоді об'єм піраміди дорівнює (кут. од.)

Відповідь: Об'єм піраміди складає 53 (кут. од.).

5. Довжина висоти, піраміди опущену на основу. Позначимо її як .

З шкільного курсу геометрії відомо, що об'єм піраміди обчислюється так:

, значить , звідси ;

Тепер підставимо значення виразу і одержимо , або

(од.).

Відповідь: Довжина висоти, піраміди опущену на основу складає (од.).

Задача 5. Задано координати точок в ПДСК А(3;4), В(-2;2). Записати їх координати в полярній системі координат.

Розв’язок: Перехід від ПДСК до полярної здійснюється за формулами:

для точки А

Для точки В .

Точка

І навпаки задані точки і в полярній системі координат. Записати їх в координати в ПДСК.

Розв’язок: Перехід від полярної системи координат до ПДСК здійснюється за формулами:

Значить, для т. С , обчислимо , значить в ПДСК т. С має координати .Для т. D

Кут в радіан знаходиться в третій четверті тригонометричного кола, в якій і синус і косинус приймають від’ємні значення:

.

Точка D в ПДСК має координати