Афінний простір. Афінна та декартова системи координат

Афінний простір

Множина точок А, для яких побудовано простір називається афінним простором, якщо виконуються умови:

1.Для будь-якої точки А ( ) і вектора існує єдина точка , така що .

2.Для трьох точок А,В,С (правило трикутника).

Введення в просторі довільного базису дозволило отримати числову характеристику вектора – координати. . Числову характеристику точки в просторі дозволить отримати в ньому системи координат. Вважають, що в просторі задана система координат, якщо вказано правило, яке встановлює відображення між точками простору і впорядкованою трійкою дійсних чисел . Назва системи координат визначається способом завдання відображення (яких існує безліч). Найбільш поширені в використанні прямолінійні: афінна(загально декартова) і Декартові.

Афінним репером називається фігура, яка складається з точки О(початку репера) і деякого базису приєднаного простору.

в репер

, в - і в -

Репер називається прямокутним(ортогональним), якщо всі його вектори попарно ортогональні,

в репер в - і в - .

Поняття пдск(прямокутна Декартова система координат)

Введемо в просторі афінну систему координат за допомогою репера . Точка О – початок репера – початок системи координат. Вісі, на яких вказано напрямки ортів називаються відповідно абсцис (відрізаний, відділений), ординат (впорядкований) і аплікат (прилеглий).

Площини, визначені парами векторів - координатні площини. Весь простір осями розбивається на вісім октантів. Прямокутна Декартова система координат (ПДСК) – система впорядкованих ортонормованих осей.

З кожною точкою М в просторі пов‘язують її радіус-вектор – вектор, який з‘єднує початок ПДСК з точкою М. Якщо , то , причому координати вектора визначені однозначно. Координатами точки М відносно реперу називаються координати радіус-вектора точки М. Числовою характеристикою точки М являються її координати .

Г еометричний зміст координат точки М. Якщо зобразити радіус-вектор точки М в фіксованій ПДСК то видно, що , , : координати точки являються скалярними проекціями радіус-вектора точки М на координатні осі.

Нехай задано дві точки і . Координати вектора знаходяться як різниця координат кінця і початку: , а довжина вектора обчислюється як радикал від суми квадратів координат .

Полярна система координат

Для побудови полярної системи координат обирається точка О – полюс і промінь ОР, який виходить із полюса – полярна вісь. На ній задається масштаб :

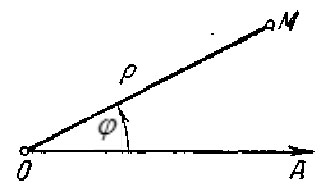
Положення будь-якої точки М площини визначається відстанню до полюса та кутом , на який потрібно повернути вісь ОР проти годинникової стрілки. - полярний радіус, - полярний кут точки М. для точки О . Числа і - полярні координати точки М. . Класично, .

Зв‘язок полярних і декартовим координат точки:

- із полярних в декартові,

- із декартовим до полярних.

Циліндричні координати. Точка

кут - азимутальний. Для точки М .

.

Сферичні координати. Точка

кут - азимутальний. Для точки М .

.

Добутки векторів
Скалярний	Векторний		Мішаний
Число, яке дорівнює добутку довжин цих векторів на косинус кута між ними.	Вектор , для якого: 1. Довжина дорівнює добутку довжин цих векторів на синус кута між ними . 2. і . 3. - трійка має ту ж орієнтацію, що і простір.		Ч исло, яке дорівнює скалярному добутку векторного добутку перших двох векторів на третій вектор .
Геометричні властивості
1. Якщо один з векторів нульовий, то їх скалярний добуток теж нульовий , або , то . 2. . 3. Вектори ортогональні тоді і тільки тоді, коли їх скалярний добуток дорівнює нулю . 4. , причому , то кут гострий, - кут тупий.	1. Векторний добуток векторів перпендикулярний площині, в якій лежать вектори . 2. Якщо , то вектори колінеарні (лінійно залежні). 3. Довжина векторного добутку векторів дорівнює площі паралелограма, побудованого на цих векторах. ,		1. - мішаний добуток векторів дорівнює орієнтованому об‘єму паралелепіпеда, побудованого на цих векторах , якщо трійка векторів - права, , якщо трійка векторів - ліва, , якщо трійка векторів - компланарні (лежать в одній площині). 2. . 3.
Алгебраїчні властивості
1. Комутативність . 2.Однорідність . 3. Адитивність . 4. .	1. Анти комутативність . 2. Однорідність . 3. Адитивність .		1. Однорідність . 2. Адитивність .
Обчислення значення (теорема)
Скалярний добуток двох векторів , заданих і базисі координатами, дорівнює сумі добутків відповідних координат . Косинуси кутів, утворених вектором з базисними векторами називається направляючими косинусами вектора, причому Очевидно, що		Якщо в базисі вектори задані координатно, то їх векторний добуток дорівнює значенню визначника Площа трикутника, побудованого на двох векторах зі спільним початком обчислюється за формулою .	Якщо в базисі вектори задані координатно, то їх мішаний добуток дорівнює значенню визначника . Зауваження. Об‘єм тетраедра, побудованого на трьох векторах . Висота паралелепіпеда при основі АВС.