Метод решения задачи об оптимальных перевозках средствами Ms Excel
Нахождение оптимального плана перевозок с применением компьютерной программы Ms Excel осуществляется посредством функции "Поиск решения".
Схема выполнения:
1. Для удобства расчетов необходимо отдельно создать матрицу, отображающую стоимость перевозок (Cij) (рис 1.), а также матрицу, которая должна будет отображать искомый план перевозок (рис. 2.).
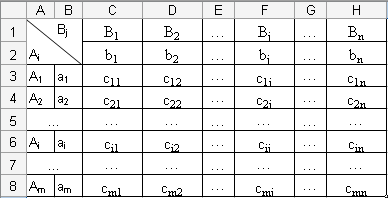
Рис. 1. Фрагмент окна программы Ms Excel: Модель таблицы «Стоимость перевозок».
2. В таблице «Стоимость перевозок» в ячейках запасов поставщиков и потребностей потребителей записать количество запасов поставщиков и потребностей потребителей соответственно, указанное в условии задачи.
3. Таблицу "План перевозок" создать с пустыми полями (заполненными единицами), заранее заданного числового формата. В ячейках запасов (потребностей) каждого поставщика (потребителя) ввести формулу, выполняющую суммирование всех возможных поставок этого поставщика (потребителя).
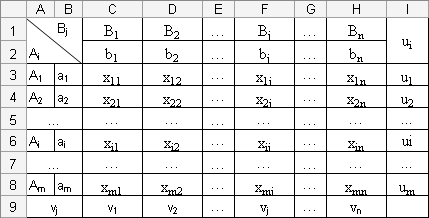
Рис. 2. Фрагмент окна программы Ms Excel: Модель таблицы «План перевозок».
4. В ячейке целевой функции ввести формулу, высчитывающую сумму произведений элементов матрицы "Стоимость перевозок" и соответствующих элементов матрицы "План перевозок".
5. В диалоговом окне функции "Поиск решения" установить необходимые ограничения, в целевой ячейке указать адрес ячейки с формулой целевой функции и установить ее равной минимальному значению, в качестве изменяемых ячеек выбрать диапазон всех элементов матрицы "План перевозок". Ограничения в "Поиске решений" заключаются в необходимости равенства запасов (потребностей), в матрице "План перевозок" соответствующим запасам и потребностям, указанным в матрице "Стоимость перевозок". Также все элементы матрицы "План перевозок" должны быть неотрицательными и целочисленными.
6. В диалоговом окне "Параметры поиска решения" установить параметр "Линейная модель" и число итераций, равное 100.
7. Выполнить функцию "Поиск решения" нажатием на кнопку "Выполнить". В качестве отчета по результатам выбрать необходимый пункт в списке "Тип отчета" диалогового окна «Результаты поиска решения».
После выполнения вышеуказанных действий при условии, что задача имеет решение, в матрице «План перевозок» запишется оптимальное решение задачи, т.е. оптимальный план перевозок с указанием объемов поставок в каждой ячейке. В ячейке с целевой функцией запишутся совокупные затраты поставок.
Задания для домашней контрольной работы
1. Математическая модель задачи Составить (не решать) математические модели приведенных задач
Для производства трех видов изделий А, В и С используется сырье типа I , II , III, причем закупки сырья I и III ограничены возможностями поставщиков. В таблице приведены нормы затрат сырья, цены на сырье и на изделия, а также ограничения по закупке сырья.
-
Тип сырья
Цена 1 кг сырья (р.)
Нормы затрат сырья на одно изделие (кг)
Ограничения по
закупке сырья (кг)
А
В
С
I
2
1
3
a
3000
II
1
4
1
3
-
III
b
6
5
2
3320
цена одного изделия (р.)
6b+12
5b+22
c
Требуется определить план производства продукции с целью максимизации прибыли:
-
a b c
a b c
a b c
a b c
1
2 1 17
6
3 1 22
11
3 3 26
16
4 2 27
2
2 2 19
7
3 2 23
12
3 4 26
17
4 3 28
3
2 3 21
8
3 2 24
13
4 1 25
18
4 3 30
4
2 4 23
9
3 2 25
14
4 1 27
19
4 4 30
5
3 1 21
10
3 3 25
15
4 2 26
20
4 4 32
1.2. Строителям требуются комплекты досок, каждый из которых состоит из а досок длиной 1,5 метра и b досок длиной 0,6 метра. Как следует распилить с четырехметровых досок, чтобы получить наибольшее количество указанных комплектов?
-
a b c
a b c
a b c
a b c
1
1 3 660
6
2 5 770
11
3 7 960
16
4 9 630
2
1 3 720
7
2 5 880
12
3 8 510
17
4 9 660
3
1 3 780
8
2 5 990
13
3 8 680
18
4 9 690
4
1 3 840
9
3 7 640
14
3 8 850
19
4 9 720
5
2 5 660
10
3 7 800
15
4 9 600
20
4 9 750