Пример использования симплекс-метода (без таблиц)

Рассмотрим следующую задачу линейного программирования:

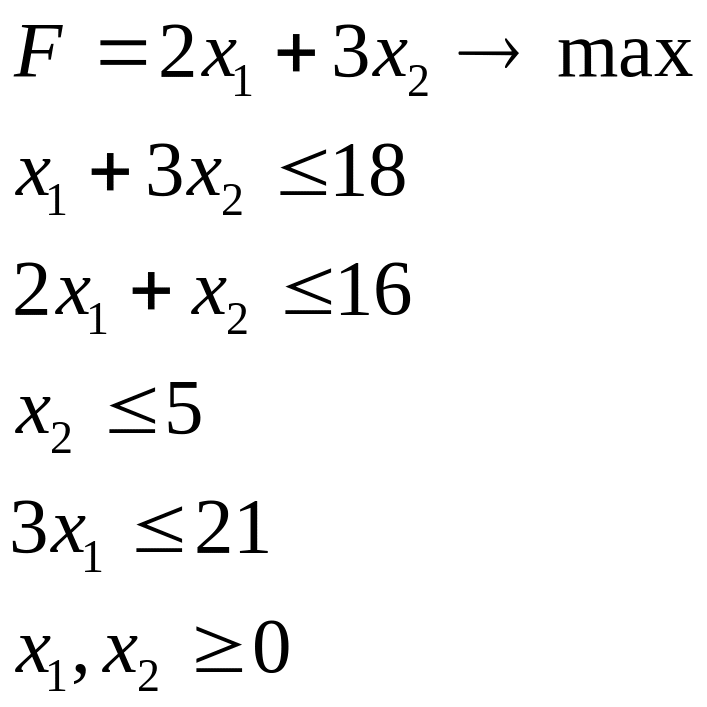
Решение. Приведем задачу к каноническому виду. Обратим имеющуюся систему функциональных неравенств в равенства, вводя для этого в каждое из них соответствующую неотрицательную переменную:

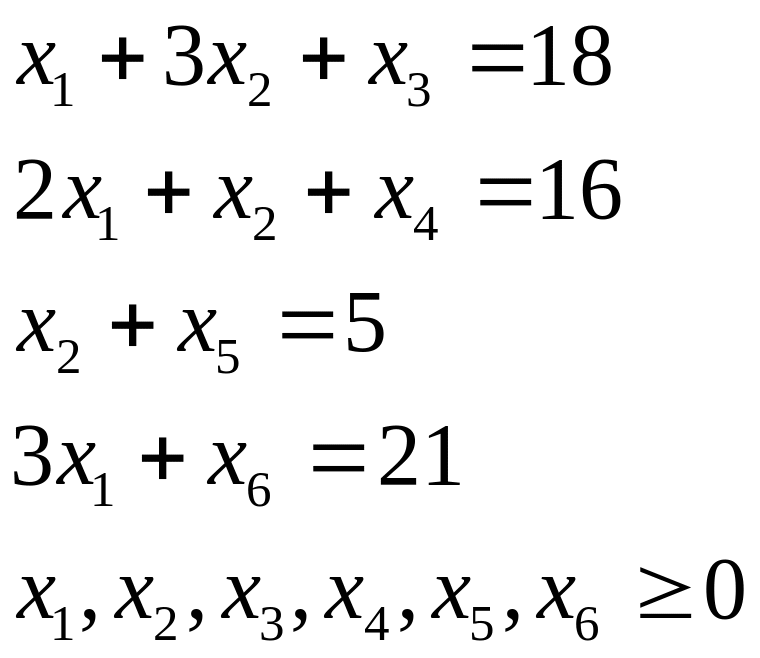
Все дополнительные переменные введены со знаком «+», так как рассматриваемые неравенства имеют знак «<=».

Для нахождения первоначального базисного решения разобьем переменные на две группы: основные и неосновные. (напомним, что базисным решением системы m линейных уравнений с n переменными называют решение, в котором все (n-m) неосновных переменных равны нулю.)

В качестве основных переменных на первом шаге нужно выбрать такие переменные, каждая из которых входит только в одно уравнение системы ограничений, и при этом нет таких уравнений системы, в которые не входит ни одна из этих переменных. Количество основных переменных равно m.

Если выбранные по этому правилу переменные имеют те же знаки, что и соответствующие им свободные члены в правых частях уравнений, то полученное таким образом базисное решение будет допустимым.

Шаг 1. определим состав основных и неосновных переменных.

В соответствии с вышеизложенным правилом:

основные переменные: ;

неосновные переменные: .

Шаг 2. Теперь, используя систему равенств, выразим основные переменные через неосновные:

.

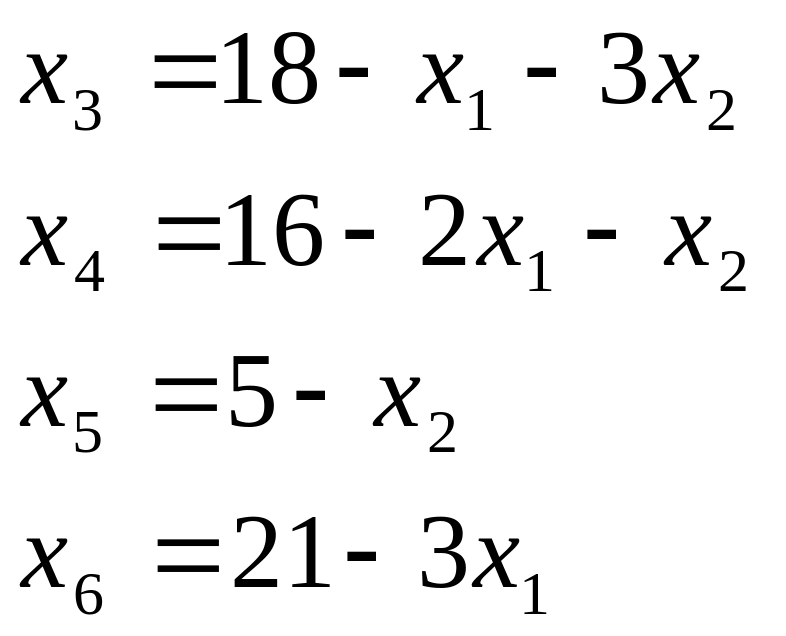Шаг 3. Положив неосновные переменные равными нулю, получим первое базисное решение:

Шаг 4. Выразим целевую функцию через неосновные переменные и определим ее значение при выбранном базисном решении:

Шаг 5. Проверим, доставляет ли выбранное базисное решение оптимум целевой функции F. Для этого воспользуемся критерием оптимальности решения при нахождении максимума функции: если в выражении линейной функции через неосновные переменные отсутствуют положительные коэффициенты при неосновных переменных, то решение является оптимальным.

В соответствии с данным критерием исследуемое базисное решение не является оптимальным, следовательно, необходимо перейти к другому базисному решению.

Шаг 6. Сформулируем основное правило перехода к лучшему (не худшему) решению: в новый состав основных переменных вводится та из неосновных, которая имеет наибольший положительный коэффициент в целевой функции.

В данном случае это коэффициент при х₂.

Чтобы новое опорное решение, с одной стороны, улучшало (или, по крайней мере, не ухудшало) значение функционала, а с другой – было бы опорным, необходимо определить:

• Как должна измениться (увеличиться) переменная х₂, вошедшая в новый состав основных переменных;

• какая переменная из «бывших основных» должна пе­рейти в новый состав неосновных переменных при пе­реходе от одного (старого) базисного решения к друго­му — новому.

Чтобы оценить, в каких пределах возможно изменение переменной х₂, необходимо определить:

при каких значениях х₂ каждая из «старых» основных переменных останется неотрицательной (соблюдение этого условия и делает новое искомое решение допустимым).

Очевидно, что для этого должны выполняться следую­щие неравенства:

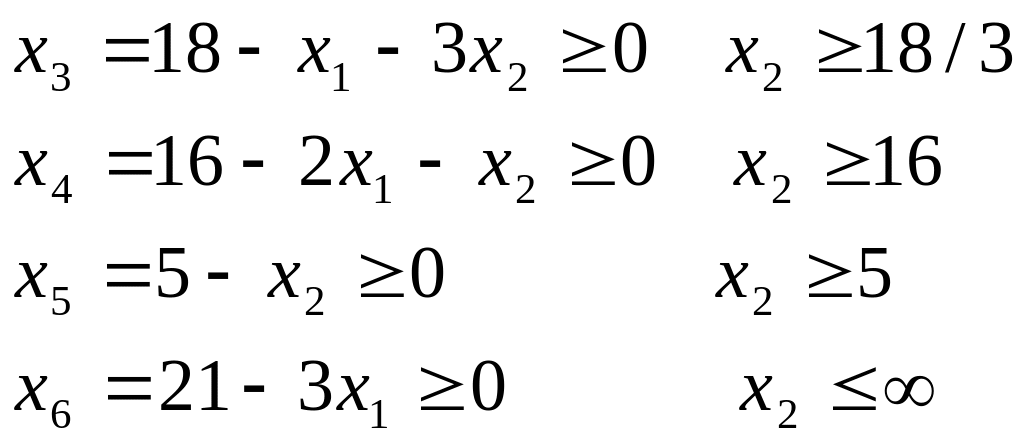
Каждое из неравенств системы определяет воз­можные границы изменения переменной х₂. В частности, из последнего неравенства системы следует, что переводимая переменная может возрастать неограниченно, т.е. ее грани­ца может быть обозначена как ∞.

Очевидно, что допустимость решения будет обеспечена только в том случае, если будут выполнены все ограниче­ния системы. В свою очередь, это условие будет со­блюдаться, если:

x₂=min{18:3; 16:1; 5:1; ∞}=5.

При х₂=5 переменная х₅ обращается в 0 и переходит в разряд не основных. Уравнение, где достигается наиболь­шее возможное значение переменной х₂, называется разре­шающим. После проделанных преобразований вновь возвращаемся к первому шагу.

Шаг 1. Определяем состав основных и неосновных пе­ременных:

основные переменные: ;

неосновные переменные: .

Шаг 2. Выразим основные переменные через неоснов­ные, воспользовавшись соотношением из разрешающего уравнения:

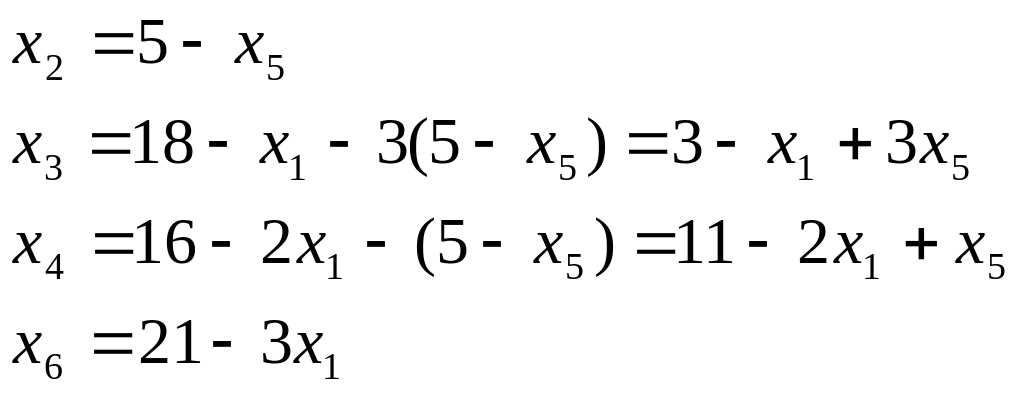
Ш аг 3. Положив неосновные переменные равными ну­лю, получим новое базисное решение :

.

Шаг 4. Выразим целевую функцию через неосновные переменные и определим ее значение при данном базисном решении:

Шаг 5. Проверим, доставляет ли выбранное базисное решение оптимум целевой функции. Коэффициент при х₁ в выражении целевой функции положителен, следовательно, данное базисное решение не доставляет оптимума целевой функции и необходимо искать новое базисное решение, которое улучшило бы (или, по крайней мере, не ухудшило бы) значение функционала.

Шаг 6. Используя сформулированное выше правило пе­рехода к лучшему решению, введем в новый состав основ­ных переменных х₁.

Определим допустимое значение х₁ и разрешающее уравнение.

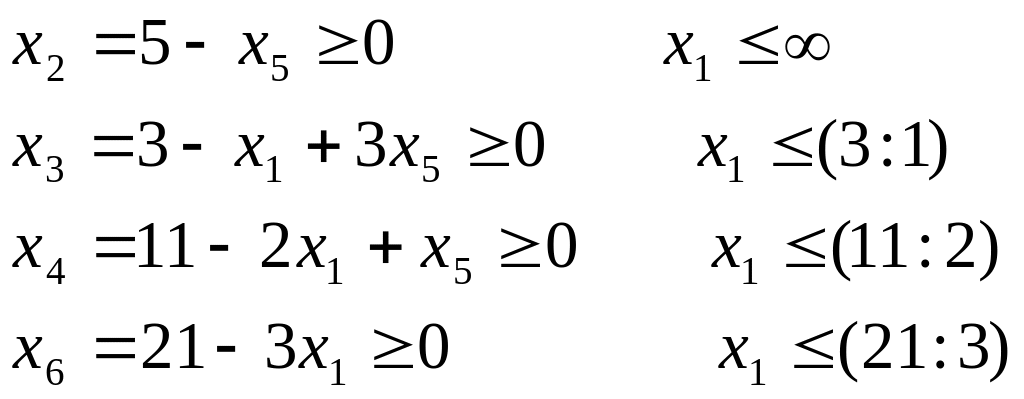
x₁=min{∞; 3:1; 11:2; 21:3}=3.

Из разрешающего уравнения следует, что если x₁=3, то х_з=0, следовательно, можно опять вернуться к первому ша­гу.

Шаг 1. Определим новый состав основных и неосновных переменных:

основные переменные: ,

не основные переменные: .

Шаг 2. Выразим основные переменные через неоснов­ные:

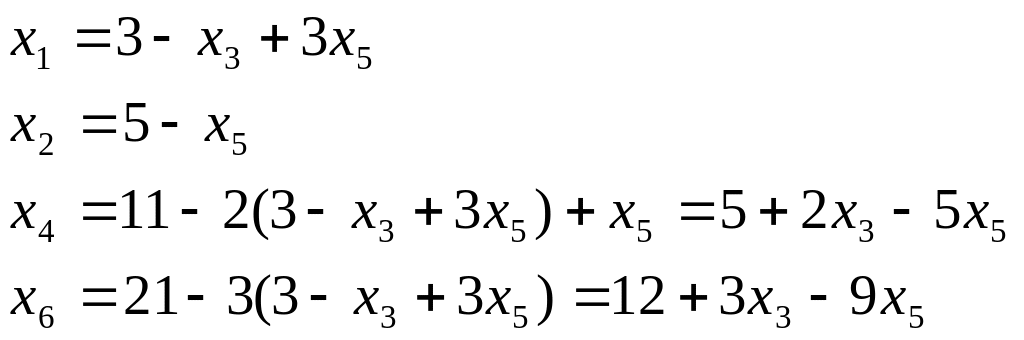
Шаг 3. Положив неосновные переменные равными ну­лю, получим новое базисное решение:

Шаг 4. Выразим целевую функцию через неосновные пе­ременные и определим ее значение при данном базисном ре­шении:

.

Шаг 5. Проверим критерий оптимальности: он опять не выполняется, так как коэффициент при х₅ положителен.

Ш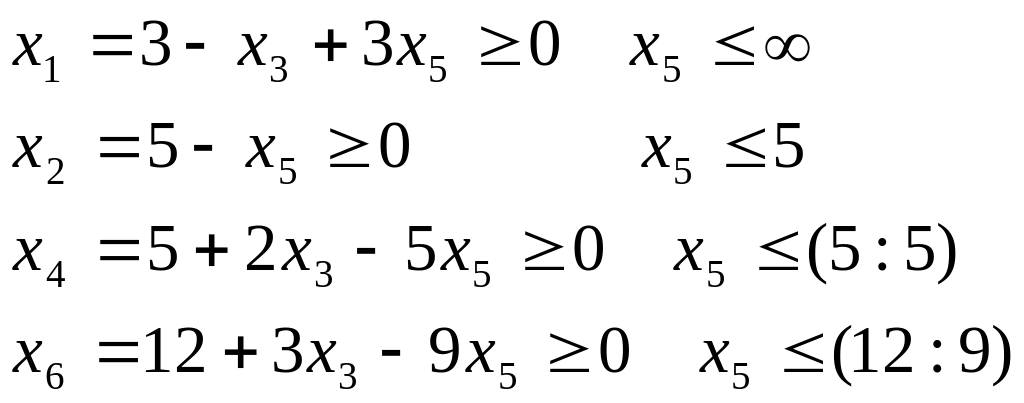 аг 6. Вновь используя сформированное выше правило перехода к лучшему решению, введем в новый состав пе­ременных х₅.

Из разрешающего уравнения следует, что при х₅=1 х₄=0, следовательно, х₄ переходит в состав неосновных перемен­ных. Вновь возвращаемся к первому шагу.

Шаг 1. Определяем новый состав переменных:

основные переменные:

неосновные переменные: .

Шаг 2. Выразим основные переменные через неоснов­ные. Воспользовавшись разрешающим уравнением, полу­чаем:

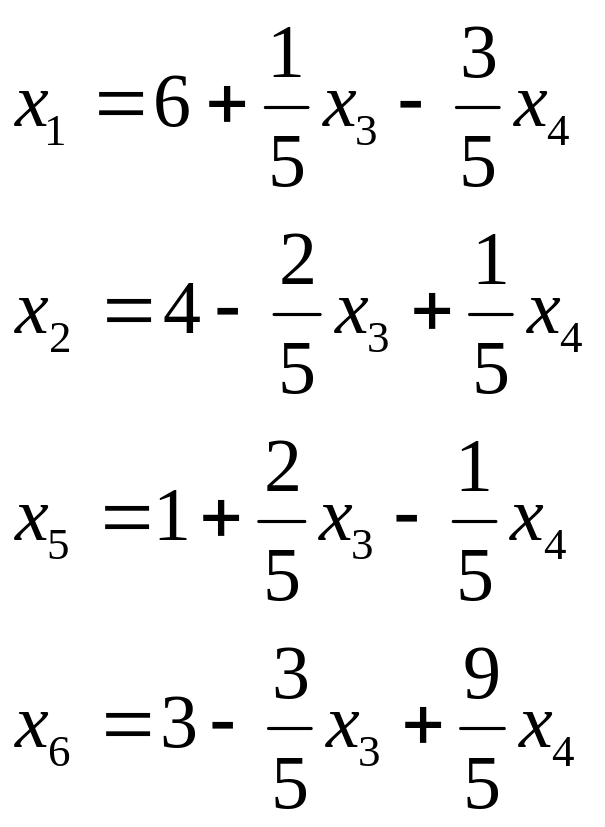
Шаг 3. Положив неосновные переменные равными ну­лю, получим новое базисное решение:

Шаг 4. Выразим целевую функцию через неосновные переменные и определим ее значение при данном базисном решении:

.

Шаг 5. Используя критерий оптимальности, приходим к выводу, что на этот раз он выполняется и что исследуемое базисное решение является оптимальным.

Данный пример показывает, что за определенное коли­чество итераций, каждая из которых содержит определен­ное число шагов, в задаче линейного программирования может быть найдено оптимальное решение.