Задачи для самостоятельного решения

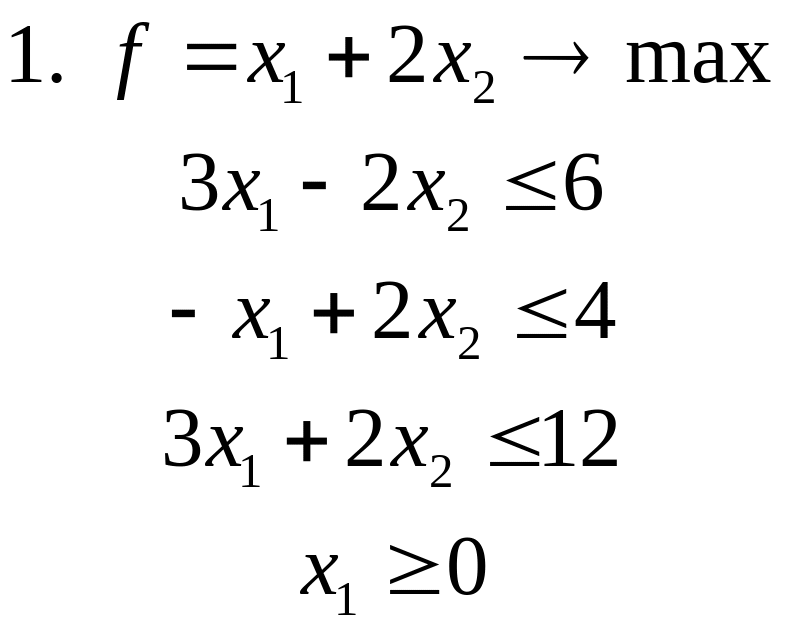
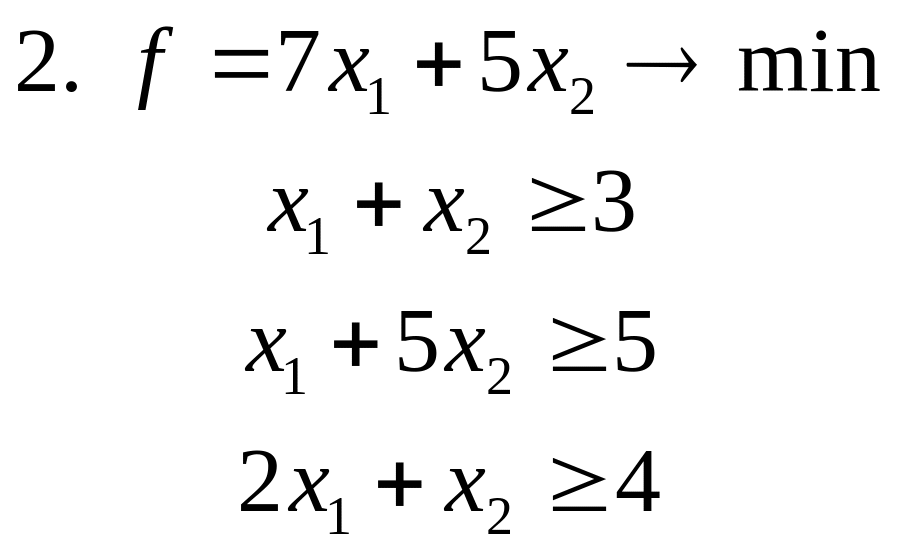
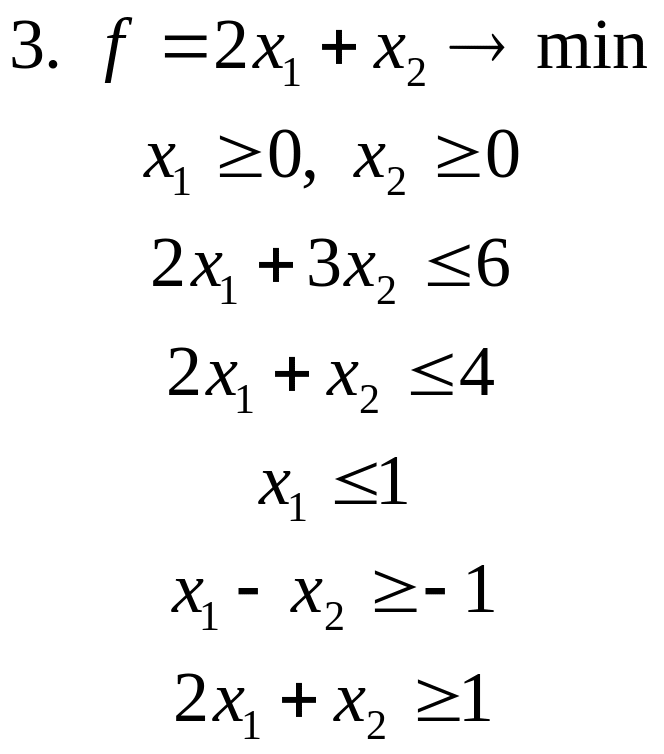
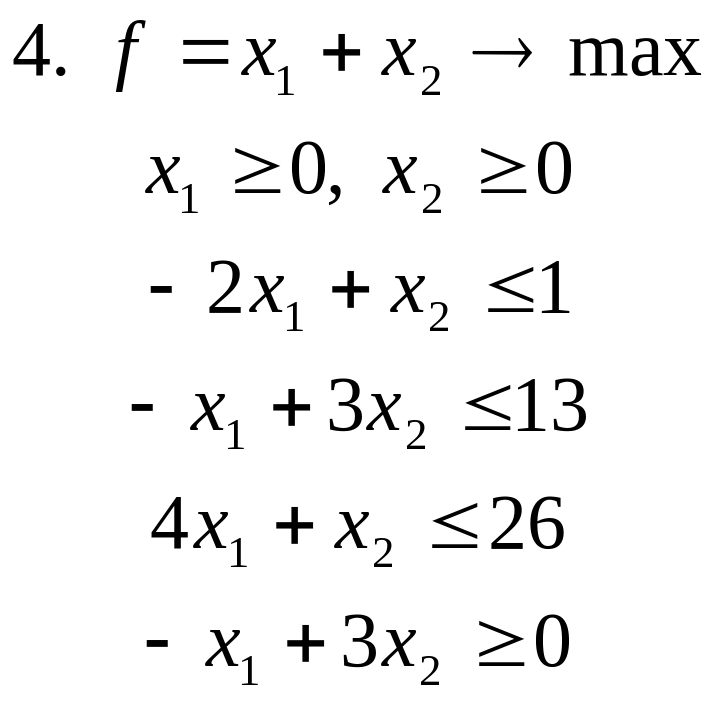
Симплекс - алгоритм

Задача должна быть приведена к канонической форме. Определить начальное базисное решение (опорный план), приравнивая к нулю (n-m) переменных (небазисных). По необходимости применить искусственные переменные.

(*)

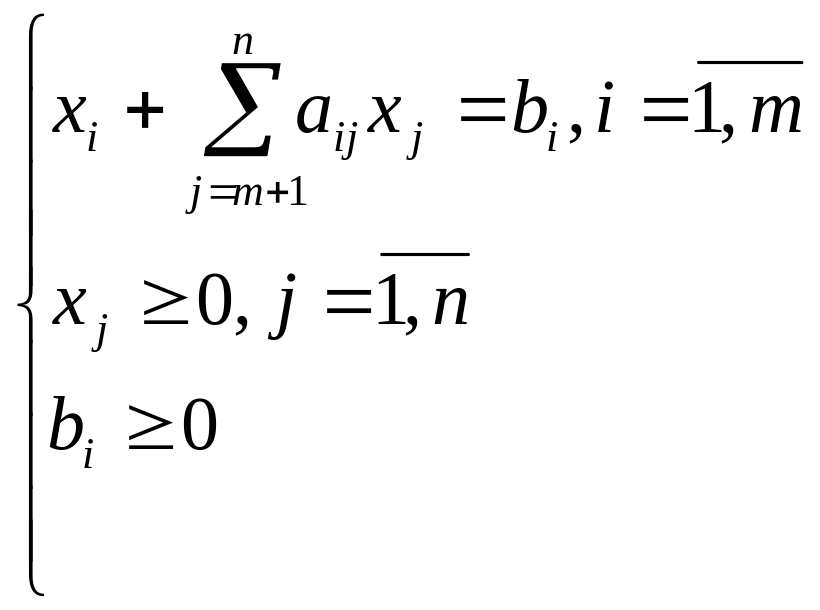Тогда опорный план - X=(x₁, x₂, …,x_m,0,…0)=( b₁, b₂, …,b_m,0,…0).

Ему соответствует значение целевой функции:

Z=c₁b₁+c₂b₂+…+ c_mb_m=

Ш1. Опорный план исследуется на оптимальность для определения направления его улучшения. Для этого строится нулевое приведенное уравнение на основе z,

базисные переменные выражаются через свободные и подставляются в выражение для целевой функции, приводятся подобные коэффициенты при переменных x_j.

,

Коэффициенты a_0j – оценки оптимальности соответствующих небазисных переменных.

Характеристика оптимальности опорного плана производится по правилам:

1. Если a_0j>=0, j=1,…,n, то опорный план – оптимальный – признак оптимальности опорного плана.

2. Если a_0j < 0, для некоторого j и все соответствующие a_ij <= 0 (i=1,…,m), то значение целевой функции не ограничено сверху на множестве планов.

3. Если a_0j < 0 для некоторых индексов j и для каждого из этих существует хотя бы одно a_ij > 0, то можно перейти к новому опорному плану, при котором z увеличивается.

Новый опорный план – новый базис – из числа небазисных переменных выбирается та, увеличение которой приводит к улучшению z:

x_k,

Если такой переменной нет, то найденный опорный план – оптимальный и вычисления завершаются.

Ш2. Из числа переменных текущего базиса выбирается исключаемая переменная, которая на последующем шаге должна стать свободной.

Для этого в k-м столбце, соответствующем переменной, включаемой в новый базис, отыскивается такая строка l, у которой a_lk > 0 и отношение постоянной b_l в правой части ограничения к a_lk - минимально:

Исключаемая переменная x_l, число a_lk – разрешающий элемент.

Ш3. Переход к новому базису. Переход к новому виду (*) относительно нового базиса с помощью подстановок или на основе формул Жордана-Гаусса:

Перейти к Ш1.

Вычислительный процесс удобно фиксировать в симплекс-таблицах.

I	БП	X1 X2 … Xm Xm+1 … Xn	bi	bi/aℓk
1	X1	1 0 …. 0 a1m+1 … a1n	b1
2	X2	0 1 …. 0 a2m+1 … a2n	b2
..		…. …
m	Xm	0 0 ….. 1 amm+1 … amn	bm
0	z	0 0 ….. 0 a0m+1 … a0n	b0

Задача. На кондитерскую фабрику г. Ступино перед Новым годом поступили заказы на подарочные наборы конфет из трех магазинов. Возможные варианты наборов, их стоимость и оставшиеся товарные запасы на фабрике представлены в таблице 8.

Определить оптимальное количество подарочных наборов, которые фабрика может предложить магазинам и обеспечить максимальный доход от продажи.

Таблица 8

Наименование конфет	Вес конфет в наборе, кг			Запасы конфет, кг
	А	В	С
Сникерс	0,3	0,2	0,4	600
Марс	0,2	0,3	0,2	700
Баунти	0,2	0,1	0,1	500
Цена, руб	72	62	76

Запишем математическую модель задачи. Пусть x₁, x₂, x₃ – количество подарочных наборов А, В и С соответственно.

Тогда определим вектор который удовлетворяет условиям:

и обеспечивает максимальное значение целевой функции