Свойства неопределенного интеграла (правила интегрирования)

1. ,

2. ,

3. ,

4. , где а – постоянная,

5. ,

6. Если и , то .

Задача 1. Найти интеграл .

Решение: Используя свойства 4 и 5, получаем

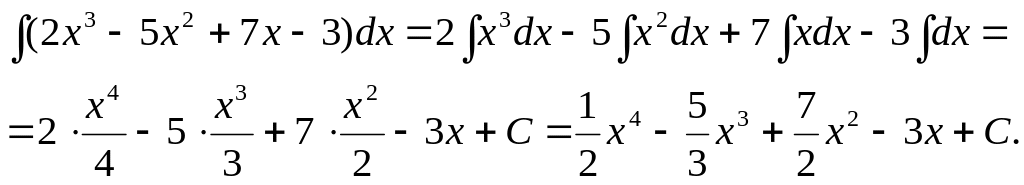
Задача 2. Найти интеграл .

Решение: Этот интеграл можно преобразовать следующим образом:

Теперь переменной интегрирования служит выражение и относительно этой переменной получается интеграл от степенной функции

=

=== =====

= .

Задача 3 Найти следующие интегралы

3.1 3.11

3.2 3.12

3.3 3.13

3.4 3.14

3.5 3.15

3.6 3.16

3.7 3.17

3.8 3.18

3.9 3.19

3.10 3.20

Практическое занятие №15

Методы замены переменных, интегрирования по частям

Если функция x=φ(t) имеет непрерывную производную, то в данном неопределенном интеграле f(x)dx всегда можно перейти к новой переменной t по формуле

 f(x)dx =  f(φ(t)) φ(t)dt, (1)

Затем найти интеграл из правой части формулы (1) (если это возможно) и вернуться к исходной переменной x. Такой способ нахождения интеграла называется методом замены переменной или методом подстановки.

Задача 1. Найти

Решение. Введем новую переменную t по формуле t = .

Тогда x = t² + 1 , dx = 2tdt

= .

Метод интегрирования по частям основан на следующей формуле:

, (1)

где u(x), (x) – непрерывно-дифференцируемые функции. Формула (1) называется формулой интегрирования по частям. Применять ее целесообразно, когда интеграл в правой части формулы более прост для нахождения, нежели исходный. Отметим, что в некоторых случаях формулу (2) необходимо применять несколько раз.

Метод интегрирования по частям рекомендуется использовать для нахождения интегралов от функций , , , , , , , arcsin x , и т.д., где n, k - целые положительные постоянные, ,  R, а так же для отыскания некоторых интегралов от функций, содержащих обратные тригонометрические и логарифмические функции.

Задача 2. Найти .

Решение. Воспользуемся методом интегрирования по частям. Положим u = x, d = e^-2xdx. Тогда du = dx, , (всегда можно считать, что С = 0). Следовательно , по формуле (2) имеем:

В некоторых случаях формула интегрирования по частям применяется несколько раз.

Задача 3. Найти Решение. .

Иногда применение формулы интегрирования по частям несколько раз не дает ответа, в этих случаях интеграл в правой части сводят к виду интеграла в левой части и из полученного выражения, как из уравнения, определяют искомый интеграл

Задача 4. Найти .

Решение.

Перенеся последний интеграл в левую часть равенства, получим

Следовательно,

Практическое занятие №16

Интегрирование простейших рациональных дробей.

Интегрирование некоторых иррациональностей

Рациональной функцией R(x) называется функция, равная отношению двух многочленов:

, (1)

Где m, n – целые положительные числа; b_i, a_j R; , .

Если mn, то R(x) называется правильной дробью, если m  n, - неправильной дробью.

Всякую неправильную дробь путем деления числителя на знаменатель можно представить в виде суммы некоторого многочлена и правильной дроби: ,

где , - многочлены; - правильная дробь; l  n.

Например, .

Так как всякий многочлен легко интегрируется, то интегрирование рациональных функций сводится к интегрированию правильных дробей. Поэтому в дальнейшем рассматрим функции R(x) при условии mn.

Простейшей дробью называется дробь одного из следующих четырех типов:

1) ; 2) ;

3) ; 4) ,

Где A, a, M, N, p, q – постоянные числа; k – целое, k  2; p²-4q  0.

Очевидно, что интегралы от простейших дробей первого и второго типов находятся легко:

Методику нахождения интегралов от простейших дробей третьего типа рассмотрим на примере:

Задача 5. Найти

Решение. Функция, стоящая под знаком интеграла является простейшей дробью, так как дискриминант выражение стоящее в знаменателе <0. Поэтому сначала выделам в числителе производную знаменателя:

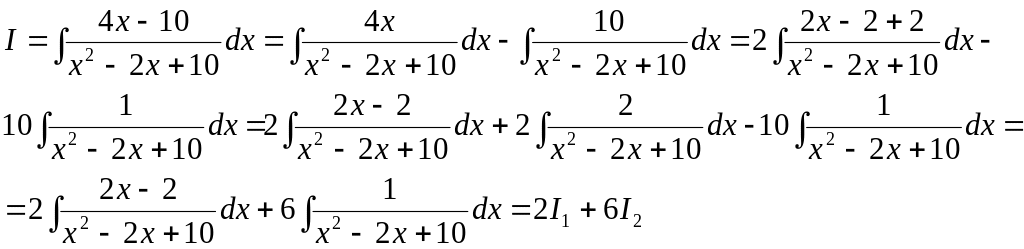
Представили интеграл в виде суммы двух интегралов, рассмотрим каждый из них по отдельности.

.

В знаменатели дроби второго интеграла выделим полный квадрат:

,

Возвращаясь к первоначальному интегралу:

.

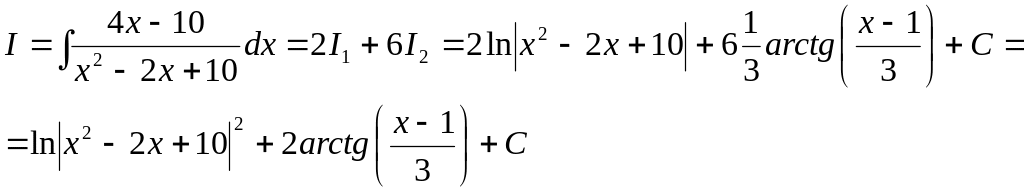Задача 6. Найти

Решение. На основании теоремы о разложении правильной дроби в сумму простейших дробей имеем: При и находим , что , , т.е. A = 1/4, B = 1/2.

Для вычисления значения C приравняем в тождестве коэффициенты при .

Получим 0 = A+C, т.е. C = -1/4.

Окончательно имеем

Интегрирование некоторых иррациональных функций.

Не для всякой иррациональной функции можно найти первообразную в виде элементарной функции. Рассмотрим интегралы от некоторых иррациональных функций, которые с помощью определенных подстановок приводятся к интегралам от рациональных функций новой переменной.

Интеграл вида

где R – рациональная функция , a, b, c, d – постоянные , r_i, s_i – целые положительные числа , , приводится к интегралу от рациональной функции новой переменной u с помощью подстановки:

( здесь число m – наименьшее общее кратное (НОК) знаменателей дробей , т.е. m = НОК ( )).

Задача 7. Найти

7.1 7.11

7.2 7.12

7.3 7.13

7.4 7.14

7.5 7.15

7.6 7.16

7.7 7.17

7.8 7.18

7.9 7.19

7.10 7.20