1. Непрерывность в точке

Определение 1. Пусть функция y=f(x) определена в точке х₀ и в некоторой окрестности этой точки. Функция y=f(x) называется непрерывной в точке х₀, если существует предел функции в этой точке и он равен значению функции в этой точке, т.е.

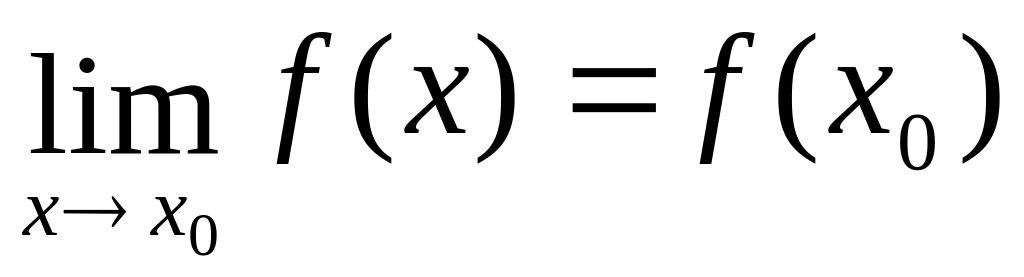
Определение 2. функция y=f(x) называется непрерывной в точке х₀, если она определена в точке х₀ и ее окрестности и выполняется равенство , где , т.е. бесконечно малому приращению аргумента соответствует бесконечно малое приращение функции.

Задача 1. Исследовать на непрерывность функцию y=sin x.

Решение. Функция y=sin x определена при любом х. Возьмем произвольную точку х и найдем приращение у:

.

Тогда , т.к. произведение ограниченной функции и бесконечно малой функции (б.м.ф.) есть б.м.ф.

2. Непрерывность функции в интервале и на отрезке.

Определение 3. Функция y=f(x) называется непрерывной в интервале (a,b), если она непрерывна в каждой точке этого интервала.

Определение 4. Функция y=f(x) называется непрерывной на отрезке [a;b], если она непрерывна в интервале (a,b) и в каждой точке х=a непрерывна справа (т.е. ), а в точке х=b непрерывна слева (т.е. ).

3. Точки разрыва функции и их классификация.

Определение 5. Точки в которых нарушается непрерывность функции называются точками разрыва этой функции.

х=х₀ – точка разрыва если не выполняется по крайней мере одно из условий определения 1, а именно:

1. функция определена в окрестности точки х₀, но не определена в самой точке. (например, ).

2. функция определена в точке х₀ и ее окрестности, но не существует предела f(x) при хх₀.

Задача 2. Задана функция у=f(x). Найти точки разрыва, если они существуют. .

Решение. Функция определена в точке х=2 (f(2)=0), однако в точке х=2 имеет разрыв, так как односторонние пределы при х2 слева и справа не равны между собой:

, .

3. функция определена в точке х₀ и ее окрестности, существует но этот предел не равен значению функции в точке х₀: .

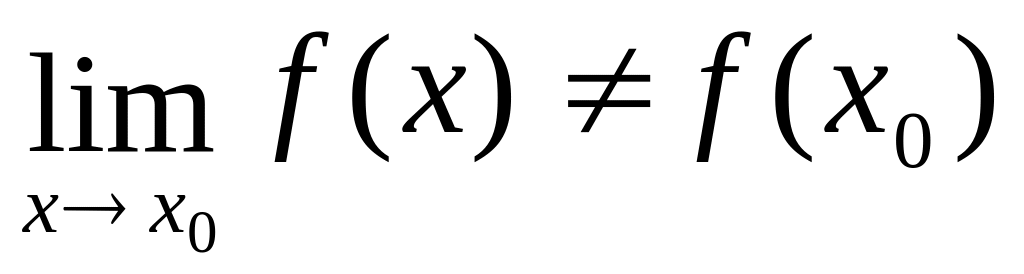Задача 3. Задана функция у=f(x). Найти точки разрыва, если они существуют. .

Решение: Здесь х₀=0 – точка разрыва: предел функции неравен значению функции в этой точке однако .

Все точки разрыва функции разделяются на точки разрыва первого и второго рода.

Определение 6. Точка х₀ называется точкой разрыва первого рода функции y=f(x), если в этой точке существуют конечные пределы функции слева и справа (односторонние пределы), т.е. . При этом:

а) если А₁=А₂, то точка х₀ называется точкой устранимого разрыва;

б) если А₁А₂, то точка х₀ называется точкой конечного разрыва.

Величину А₁–А₂ называют скачком функции в точке разрыва первого рода.

Определение 7. Точка называется точкой разрыва второго рода функции y=f(x), если по крайней мере один из односторонних пределов (слева или справа) не существует или равен бесконечности.

Задача 4. Задана функция у=f(x) и два значения аргумента x₁ и x₂. Требуется:

1) установить, является ли данная функция непрерывной или разрывной для каждого из данных значений аргумента;

2) в случае разрыва функции найти ее пределы в точке разрыва слева и справа;

3) сделать схематический чертеж.

4.1. f(x)=5^2/(2–x) x₁=0 x₂=2 4.2. x₁=0 x₂=1

4.3. f(x)=11^1/x x₁=0 x₂=4 4.4. f(x)=3^1/(7–x) x₁=1 x₂=7

4.5. f(x)=4^2/(1+x) x₁=0 x₂= –1 4.6. x₁=1 x₂=2

4.7. x₁=0 x₂= –4 4.8. x₁=1 x₂=5

4.9. x₁=1 x₂= –2 4.10. x₁=3 x₂=2

Задача 5. Задана функция у=f(x). Найти точки разрыва, если они существуют. Сделать чертеж.

5.1. f = 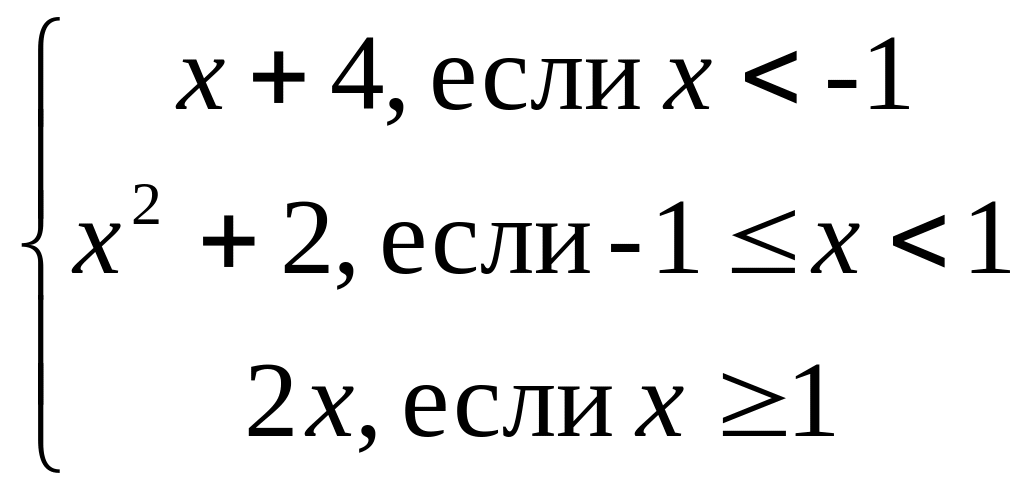. 5.2. .

5.3. f . 5.4. f .

5.5. f . 5.6. f(x) = .

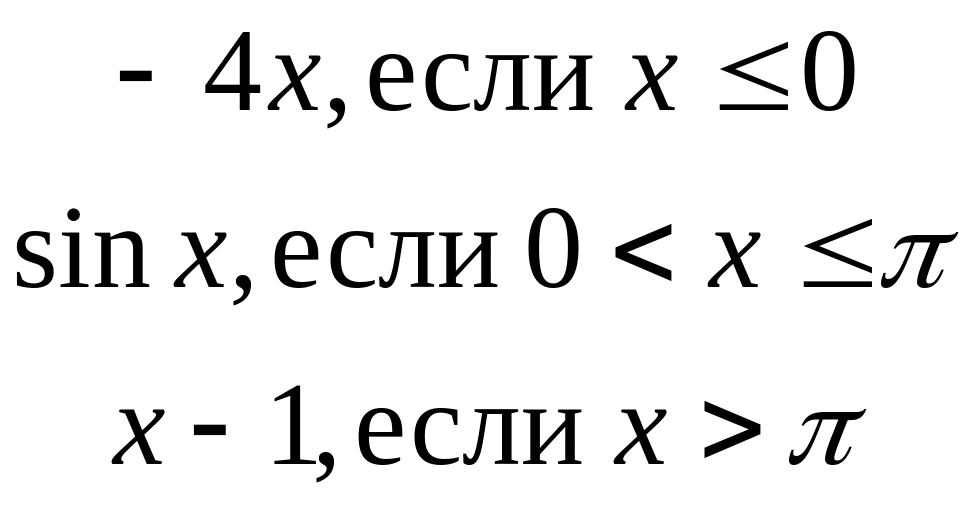5.7. f(x) = . 5.8. f(x) = .

5.9. . 5.10. f .

Практическое занятие №7

Производная. Геометрический, механический смысл. Техника дифференцирования. Производная сложной функции

1. Правила нахождения производных и дифференцирования ( ).

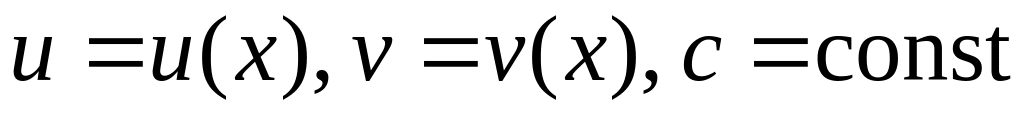, если (производная сложной функции)

, если (производная обратной функции)

(формула логарифмического дифференцирования)

1. (постоянная)

2. (степенная)

3. (показательная)

4. (экспонента)

5. _{(логарифмическая)}

_6.

_{Тригонометрические Обратные тригонометрические}

7. 11.

_{8. 12.}

9. 13.

10. 14.

Задача 1. Найти производную функции: Решение: .

По правилу нахождения производной от суммы:

(u+v)=u+v

Получили сумму производных от сложных функций. Пусть ,

=

= =

=

По формуле производной от сложной функции

= =

= = –

– = – = – .

Задача 2. Найти производные

2.1 2.2

2.3 2.4

_{2.5 2.6}

2.7 2.8 .

_2.9 . 2.10

2.11 2.12

2.13 2.14

2.15 2.16

2.17 2.18

2.19 2.20

2.21 2.22

2.23 _2.24

2.25 2.26

2.27 2.28

2.29 2.30

2.31 2.32

2.33 2.34

2.35 2.36

Практическое занятие №8

Логарифмическое дифференцирование.

Производная параметрически заданной функции, неявной функции

Иногда, прежде чем находить производную от заданной функции, ее необходимо преобразовать, чтобы процесс дифференцирования упростился. Например, функции вида , где , сначало целесообразно прологарифмировать:

.

По свойству логарифма: . Дифференцируя последнее выражение, получим:

.

Умножим обе части на : .

Заменяя через , получим: .

При отыскании производной функции вида , следует пользоваться методом логарифмирования или применять последнюю формулу.

Задача 1. Найти производную функции .

Решение: прологарифмируем обе части равенства: . По свойству логарифмов:

.

Дифференцируя полученное равенство, имеем:

,

.

Заменяя на , получим: .

Производная функции заданной параметрически где t – вспомогательная переменная, называемая параметром, вычисляется по формуле :

.

Для нахождения производной функции, заданной неявно, нужно продифференцировать по переменной х обе части уравнения, считая при этом у функцией от х, а затем полученное уравнение разрешить относительно у .

Задача 2. Найти производную: .

Решение. В данном случае функциональная зависимость задана в неявном виде. Для нахождения производной нужно продифференцировать по переменной х обе части уравнения, считая при этом у функцией от х, а затем полученное уравнение разрешить относительно у :

Из последнего уравнения находим у : .

Задача 3. Найти производные следующих функций:

3.1 3.11

3.2 3.12

3.3 3.13

3.4 3.14

3.5 3.15

3.6 3.16

3.7 3.17

3.8 3.18

3.9 3.19

3.10 3.20

Задача 4. Найти производные следующих функций, предварительно преобразовав их:

4.1 4.9

4.2 4.10

4.3 4.11

4.4 4.12

4.5 4.13

4.6 4.14

4.7 4.15

4.8

Задача 5. Найти производные функций заданных неявно.

5.1

5.2

5.3

5.4

5.5

Задача 6. Найти для функций заданных параметрически

1. 

2. 

3. 

7.4

7.5

Практическое занятие №9

Дифференциал. Основные правила дифференцирования. Применение дифференциала в приближенных вычислениях

Пусть .

I. Правила дифференцирования	II. Формулы дифференцирования
1. 2. 3. 4. 5.	1. 2. 3. 4. 5. 6. 7.

Задача 1. Найти дифференциал функции .

Решение. .

Задача 2. Вычислить приближенно значение .

Решение. Рассмотрим функцию . Пологая , и применяя формулу получаем

.

Задача 3 Найти дифференциалы следующих функций

3.1  3.16 

3.2 3.17 

3.3  3.18 ;

3.4  3.19 

3.5 ; 3.20 

3.6  3.21 ;

3.7 ; 3.22 ;

3.8 ; 3.23 ;

3.9 ; 3.24 ;

3.10 ; 3.25 ;

3.11 ; 3.26 ;

3.12 ; 3.27

3.13 ; 3.28 ;

3.14 ; 3.29 ;

3.15 ; 3.30

Задача 4. Вычислить приближенное значение площади круга, радиус которого равен 3,02 м.

Задача 5. Найти приближенное значение объема шара радиуса 2,01м.

Задача 6. Найти приближенные значения:

а) ; б) ; в) ; г) .

Практическое занятие №10

Производные высших порядков. Формула Лейбница.

Правило Лопиталя и вычисление пределов

Производную от производной данной функции, если она существует, называют производной второго порядка, или второй производной, от данной функции и обозначают символом . Таким образом .

В общем случае производной порядка от данной функции называется производной от производной порядка этой функции:

.

Задача 1. Найти третью производную от функции .

Решение. Найдем первую производную от заданной функции . Вторая производная – это производная от производной , тогда искомая третья производная – это .

Задача 2. Найти для следующих функций

2.1 2.2

2.3 2.4

2.5 2.6

2.7 2.8

2.9 2.10

2.11 2.12

2.13 2.14

2.15

Практическое занятие №11

Монотонность, экстремумы функции

Дифференцируемая функция является монотонно возрастающей на интервале (a, b) тогда и только тогда, когда , и монотонно убывающей, если .

Точка называется критической точкой, если имеет место одно из условий:

1) ; 2) ; 3) функция в точке определена, но не существует.

Первое достаточное условие экстремума. Если при переходе через критическую точку первая производная меняет знак, то данная точка является точкой экстремума.

Критическая точка является точкой максимума, если при переходе через данную точку производная меняет знак с «+» на «–» и точкой минимума, если – с «–» на «+».

Второй достаточный признак экстремума. Если в критической точке функция f(x) дважды дифференцируема и если при этом f"(x₀) 0, то есть точка экстремума функции f(x):

точка максимума при f"(x₀)<0,

точка минимума при f"(x₀)>0.

Задача 1. Найти экстремумы функции f(x)=x³–3x²–9x+11.

Решение. Находим f'(x)=3x²– 6x–9. Производная определена на всей оси Ох; поэтому критическими точками будут только те точки, где f'(x)=0, т. е. действительные корни уравнения 3x²– 6x– 9=0, или x²– 2х– 3=0.

Решая это уравнение, находим две критические точки: х₁= -1, x₂=3. В промежутках (- , -1), (-1, 3), (3, + ) производная f(x) непрерывна и не обращается в нуль, в силу чего сохраняет в каждом из них постоянный знак. Подставляя в выражение f'(x) любые значения х, взятые из этих промежутков, определяем знаки f'(x) в них. Выбираем, например, значения х=-2, 0 и 4, лежащие в этих промежутках, и вычисляем

f' (-2) = 15; f'(0)=-9; f'(4) = 15.

Таким образом, в промежутке (- , -1) производная f(x) сохраняет знак f'(-2), т. е. положительна; аналогично устанавливаем, что в промежутке (-1, 3) она отрицательна, а в промежутке (3, -) — снова положительна.

Таким образом, в первой критической точке х₁=-1 производная f'(x) изменяет знак с «+» на «–»; поэтому при х₁=-1 f(x) имеет максимум, равный f(-1)=16.

Во второй критической точке x₂=3 производная f'(x) изменяет знак с «–» на «+»; поэтому при x₂=3 f(x) имеет – минимум, равный f(3)= -16.

Тот же результат нам даст исследование этих критических точек по второму достаточному признаку. В самом деле, f"(x)=6x-6=6(х-1); подставляя во вторую производную критические точки, т. е. значения х₁= -1 и х₂=3, находим f" (-1)= -12; f" (3)= + 12; это показывает, что точка х₁= -1 есть точка максимума, а точка x₂= -3 - точка минимума.

Практическое занятие №12

Выпуклость, вогнутость, точки перегиба. Асимптоты.

Построение графиков функций

Кривая вогнута вверх (выпукла) на интервале (a, b), если в каждой точке этого интервала выполнено условие и вогнута вниз, если .

Точка называется точкой перегиба, если касательная, проведенная в точке , делит кривую на две части, лежащие в некоторой окрестности точки касания по разные стороны от касательной. Подобно тому как точки экстремума отделяют интервалы возрастания и убывания функции, так точки перегиба отделяют интервалы постоянного направления вогнутости кривой.

Точка называется критической точкой II рода, если в этой точке имеет место одно из следующих условий:

1) ; 2) ; 3) функция в точке определена, но не существует.

Чтобы установить, является ли точка точкой перегиба руководствуются следующим правилом: если при переходе через критическую точку II рода вторая производная функции меняет знак, то данная точка является точкой перегиба.

Задача 1. Найти точки перегиба графика функции f(x)=x₃ - 3x² - 9x+11. Решение. Находим f"(x)=6(x – 1). Отсюда видно, что f"(x) обращается в нуль только при х=1 и изменяет при этом знак с «–» на «+». В этой точке y=f(1)=0. Поэтому в точке М (1; 0) график функции имеет перегиб.

Прямая называется вертикальной асимптотой кривой, если выполняется одно из условий:

1. , 2. .

Прямая является наклонной асимптотой кривой , если выполнены условия:

, или , .

Частным случаем наклонной асимптоты при и является горизонтальная асимптота.

Задача 2. Найти уравнения асимптот кривой .

Решение. Кривая имеет вертикальную асимптоту , так как . Эта кривая имеет еще горизонтальную асимптоту , при и при , так как .

При построении графика функции полезно выяснить его характерные особенности. Для этого надо:

1. найти область определения функции;

2. исследовать функцию на четность, нечетность и периодичность;

3. найти точки пересечения графика с осями координат;

4. исследовать функцию на непрерывность; найти точки разрыва (если они существуют) и установить характер разрыва; найти асимптоты кривой ;

5. найти интервалы возрастания и убывания функции и ее экстремумы;

6. найти интервалы выпуклости и вогнутости кривой и ее точки перегиба.

Задача 3. Исследовать функции методами дифференциального исчисления и построить их графики.

3.1. 3.2. 3.3.

3.4. 3.5. 3.6.

3.7. 3.8. 3.9.

3.10. 3.11. 3.12.

3.13. 3.14. 3.15.

3.16. 3.17. 3.18.

3.19. 3.20. 3.21.

3.22. 3.23. 3.24.

3.25. 3.26. 3.27.

3.28. 3.29. 3.30.

Практическое занятие №13

Формула Тейлора и ее использование в приближенных вычислениях

Формула Тэйлора дает возможность приближенно представить произ­вольную функцию , раз дифференцируемую в окрестности некоторой точки , в виде многочлена -й степени относительно разности , называемого многочленом Тэйлора, и дать оценку погрешности этого приб­лижения.

В силу этого формула Тэйлора, помимо большого числа ее теоретиче­ских применений, является основой приближенных вычислений математи­ческого анализа, поскольку многочлен, приближенно представляющий функ­цию общего вида, является выражением, числовые значения которого всегда и легко вычислимы.

Разложение многочлена -ой степени по степеням разности :

. (1)

называется формулой Тэйлора для многочлена -й степени, а коэффициенты многочлена в правой части этой формулы , , ,…, называются коэффициентами Тэилора.

, (2)

где ; (или ) называется формулой Тэйлора для функции , раз дифференцируемой в окрестности точки , с остаточным чле­ном, в форме Лагранжа.

Остаточный член формулы Тэйлора в форме Лаг­ранжа:

. (3)

где ; (или ).

При получаем как частный случай формулы Тэйлора форму­лу Маклорена:

, (4)

Формулой Тэйлора с остаточным членом в форме Пеано. (Остаточный член в форме Пеано можно получить, не требуя непрерывность в точке ) имеет вид:

. (5)

Задача 1. Вычислить значение е с точностью до 0,0001.

Решение. Представим е, как функцию , где х=1. Найдем производные , ,…, (при всяком ); , .

Поэтому по формуле (4) находим . Применим это разложение для вычисления числа с точностью до . Положим в последнем равенстве :

.

Чтобы ошибка не превосходила , надо определить из условия, чтобы остаточный член, т.е. , был меньше . Поскольку , ; поэтому уже при имеем .

Итак, можно положить

Значение числа с пятью знаками после запятой есть ..., что подтверждает правильность нашего вычисления.

Практическое занятие №14

Первообразная. Методы интегрирования разложением

Таблица интегралов

1. 9.

2. 10.

3. 11.

4. 12.

5. 13.

6. 14.

7. 15.

8. 16.