
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ
Федеральное
ГОСУДАРСТВЕННОЕ автономное ОБРАЗОВАТЕЛЬНОЕ УЧЕРЕЖДЕНИЕ
ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРаЗОВАНИЯ
СЕВЕРО - КАВКАЗСКИЙ ФЕДЕРАЛЬНЫЙ УНИВЕРСИТЕТ
МЕТОДИЧЕСКИЕ УКАЗАНИЯ
к практическим занятиям по дисциплине «Математический анализ»
для студентов по направлению подготовки 080100.62 – Экономика
Часть 1.
г. Ставрополь, 2013
Методические указания составлены в соответствии с ГОС ВПО, рабочим учебным планом и программой дисциплины «Математический анализ» для студентов по направлению подготовки 080100.62 – Экономика.
Методические указания предназначены для ознакомления студентов с основными фактами математического анализа, содержат теоретическое обоснование, задачи и рекомендуемую литературу по дисциплине.
Составители: канд. физ.-мат. наук, профессор Адамчук А. С.,
канд. физ.-мат. наук, доцент Амироков С.Р.
Рецензент: доктор физ.-мат. наук, профессор Толпаев В.А.
Содержание
Практическое занятие 1. Множества, операции над ними. Функция, график функции. Классы функций……….…………………………......................……5
Практическое занятие 2. Последовательность и ее предел. Монотонная последовательность. Число «е». Раскрытие неопределенностей. Бесконечные пределы…………..……………………..…………………………………………7 Практическое занятие 3. Предел функции. Бесконечно малые и бесконечно большие……………………………………………………….…………………..9 Практическое занятие 4. Первый замечательный предел …………………12
Практическое занятие 5, 6. Непрерывность функции в точке. Локальные свойства непрерывной функции. Точки разрыва. Глобальные свойства непрерывных функций………………………………………………….…….....13
Практическое занятие 7. Производная. Геометрический, механический смысл. Техника дифференцирования. Производная сложной функции……17
Практическое занятие 8. Логарифмическое дифференцирование.
Производная параметрически заданной функции, неявной функции…….. .20
Практическое занятие 9. Дифференциал. Основные правила дифференцирования. Применение дифференциала в приближенных вычислениях…………………………………………………………………….24
Практическое занятие 10. Производные высших порядков. Формула Лейбница. Правило Лопиталя и вычисление пределов……………..………..26
Практическое занятие 11. Монотонность, экстремумы функции………...27
Практическое занятие 12. Выпуклость, вогнутость, точки перегиба. Асимптоты. Построение графиков функций……….………………………….29
Практическое занятие 13. Формула Тейлора и ее использование в приближенных вычислениях ……………………………….………………….31
Практическое занятие 14 Первообразная. Методы интегрирования разложением…………………………………….……………………………….34 Практическое занятие 15. Методы замены переменных, интегрирования по частям ………………………….………………………………..……………….36
Практическое занятие 16. Интегрирование простейших рациональных дробей. Интегрирование некоторых иррациональностей ……..…………….38
Рекомендуемая литература………………….…………………………….…42
Практическое занятие №1
Множества, операции над ними. Функция, график функции. Классы функций
Пересечением множества А и В называется новое множество С, содержащее те и только те элементы, которые входят в оба множества А и В.
Пересечение множеств называется также их произведением. Обозначают Х = АВ или Х= АВ.
Задача 1. Найти пересечение множеств А = {2,3,7,8,10}, В = {1,3,5,6,8,9}.
Решение. Пересечением будет множество С=АВ = {3,8}.
Объединением множеств А и В называется множество С, состоящее из тех и только тех элементов, которые входят хотя бы в одно из этих множеств. Объединение множеств называется также суммой.
Обозначают так: С= АВ или С= А + В.
Задача 2. Найти объединение множеств А={1;7;5}, В={1;3;17}.
Решение. Объединением
множеств будет С=А
![]() В={1;3;7;5;17}.
В={1;3;7;5;17}.
Разностью двух множеств А и В называется такое множество С= А\В, в которое входят все элементы из А, не принадлежащие множеству В.
Множество M называется областью определения функции. Очень часто при задании функции область определения этой функции не указывается. В таком случае под областью определения функции понимают область существования аналитического выражения y=f(x), т. е. множество значений аргумента x для которых аналитическое выражение имеет определенное конечное значение.
Задача 3. Найти
область определения функции
![]() .
.
Решение. Даная
функция существует, если
![]() . Решением этого неравенства будет
отрезок [-1;1], значит функция определена
на отрезке [-1;1].
. Решением этого неравенства будет
отрезок [-1;1], значит функция определена
на отрезке [-1;1].
Задача 4. Найти область определения функций:
4.1
![]() 1.16
1.16
![]()
4.2
![]() 4.17
4.17
![]()
4.3
![]() 4.18
4.18
![]()
4.4
![]() 4.19
4.19
![]()
4.5
![]() 4.20
4.20
![]()
4.6
![]() 4.21
4.21
![]()
4.7
![]() 4.22
4.22
![]()
4.8
![]() 4.23
4.23
![]()
4.9
![]() 4.24
4.24
![]()
4.10
![]() 4.25
4.25
![]()
4.11
![]() 4.26
4.26
![]()
4.12
![]() 4.27
4.27
![]()
4.13
![]() 4.28
4.28
![]()
4.14
![]() 4.29
4.29
![]()
4.15
![]() 4.30
4.30
![]()
Практическое занятие №2
Последовательность и ее предел. Монотонная последовательность. Число «е». Раскрытие неопределенностей. Бесконечные пределы
Число «а»
называется пределом числовой
последовательности {xn},
если для любого сколь угодно малого
числа
![]() найдется
такой номер N,
зависящий от
найдется
такой номер N,
зависящий от
![]() ,
что для всех членов числовой
последовательности, начиная с n>N
выполняется неравенство
,
что для всех членов числовой
последовательности, начиная с n>N
выполняется неравенство
![]() ,
т.е. предел xn
равен a.
,
т.е. предел xn
равен a.
![]()
Раскрытие
неопределенностей вида
![]() состоит в делении числителя и знаменателя
на x
в наивысшей степени. При
этом:
состоит в делении числителя и знаменателя
на x
в наивысшей степени. При
этом:
если старшая степень переменной в числителе и знаменателе одинаковы, то предел равен конечному числу, а именно отношению коэффициентов при старших степенях;
если старшая степень числителя ниже старшей степени знаменателя, то предел равен нулю;
если старшая степень числителя выше старшей степени знаменателя, то предел равен
 .
.
Задача 1.Вычислить
предел: ![]()
Решение: Числитель и знаменатель дроби – бесконечно больше функции, поэтому здесь имеет место неопределенность вида . Раскрывая эту неопределенность, поделим числитель и знаменатель дроби на старшую степень x, т.е. на x2:
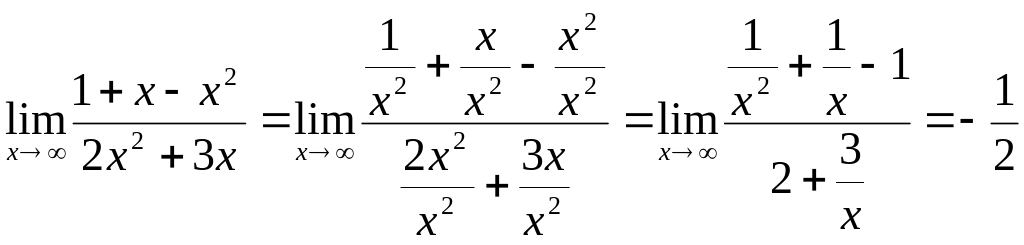 .
.
[Учитываем, что
функции
![]() и
и
![]() - бесконечно малые при
- бесконечно малые при
![]() ]
]
Второй замечательный предел.
![]() (1 форма)
(1 форма)
![]() (2 форма)
(2 форма)
Задача 2. Вычислить
предел: ![]()
Решение: Имеем
неопределенность вида (1![]() ).
Выражение под знаком предела преобразуем
так, чтобы задача сводилась ко второму
замечательному пределу:
).
Выражение под знаком предела преобразуем
так, чтобы задача сводилась ко второму
замечательному пределу:
![]() =степень
домножим и разделим на выражение
=степень
домножим и разделим на выражение
![]() =
=![]()
=выражение
![]() (второй
замечательный предел)=
(второй
замечательный предел)=
=![]() =
=![]() =
=![]() .
.
Задача 3. Найти следующие пределы
3.1.
![]() ;
3.16
;
3.16
![]() ;
;
3.2
![]() 3.17
3.17
![]() ;
;
3.3
![]() ;
3.18
;
3.18
![]() ;
;
3.4
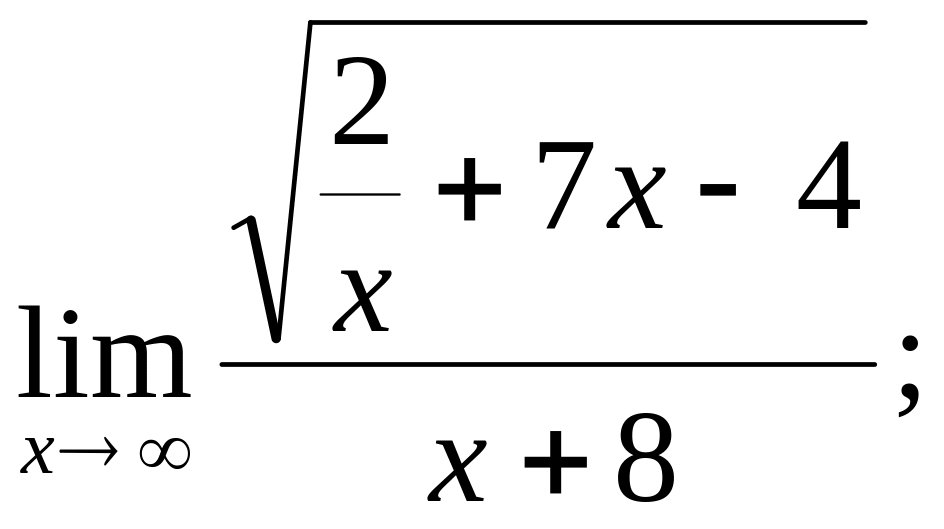 3.19
;
3.19
;
3.5
![]() 3.20
3.20
![]() ;
;
3.6
![]() ;
3.21
;
3.21
![]() ;
;
3.7
 ;
3.22
;
3.22
![]() ;
;
3.8
 3.23
3.23
![]() ;
;
3.9
![]() 3.24
3.24
 ;
;
3.10
3.25
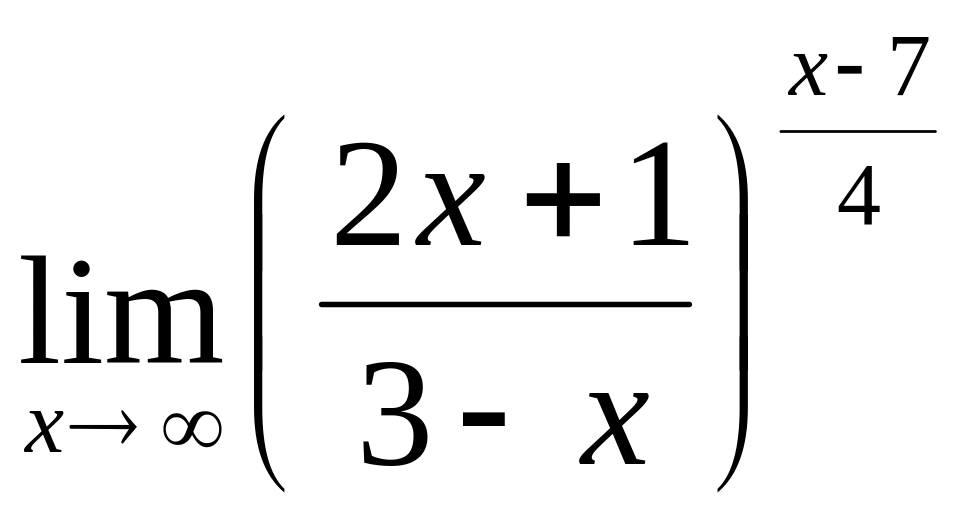 ;
;
3.11
![]() 3.26
3.26
![]() ;
;
3.12
![]() 3.27
3.27
![]() ;
;
3.13
3.28
![]() ;
;
3.14
;
3.29
![]() .
.
3.15
;
3.30
![]()
Практическое занятие №3
Предел функции. Бесконечно малые и бесконечно большие
Число А называется пределом функции y = f(x), в точке x0 (при стремлении x к x0), если для любого, сколь угодно малого числа
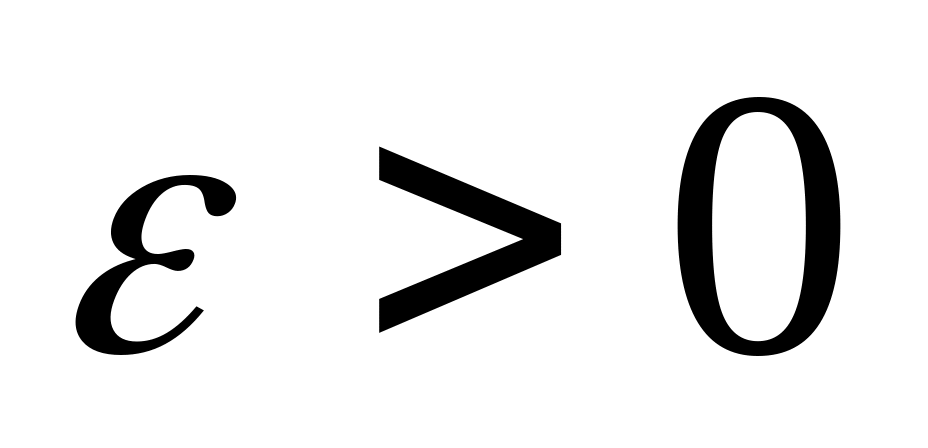 найдется
такое положительное число
найдется
такое положительное число
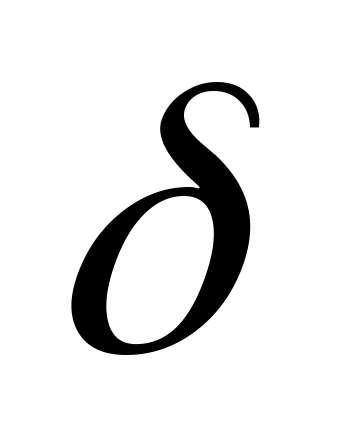 ,
зависящее от
,
что для всех x,
удовлетворяющих условию
,
зависящее от
,
что для всех x,
удовлетворяющих условию
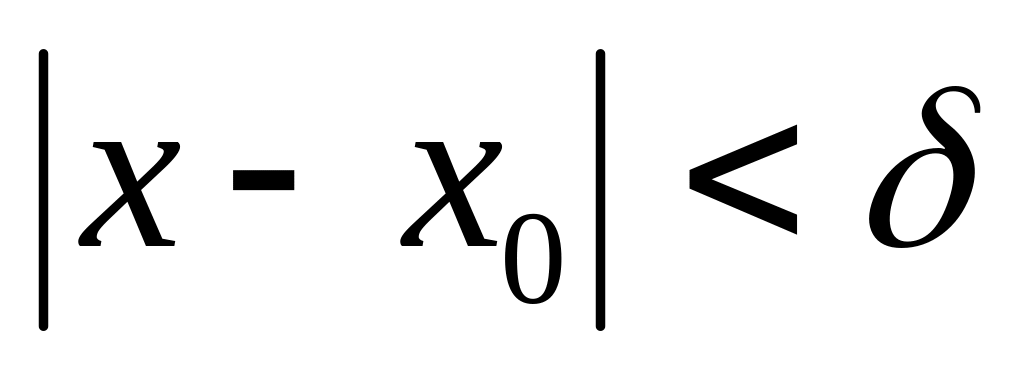 , x
, x ,
выполняется неравенство
,
выполняется неравенство
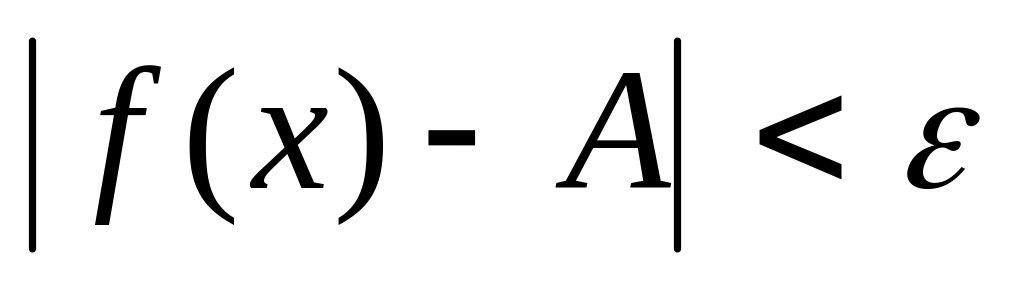 .
.
![]()
![]() .
.
Число А1 называется пределом функции y = f(x) слева, в точке x0, если для любого, сколь угодно малого числа существует =( ), такое что при x(х0–; х0), выполняется неравенство
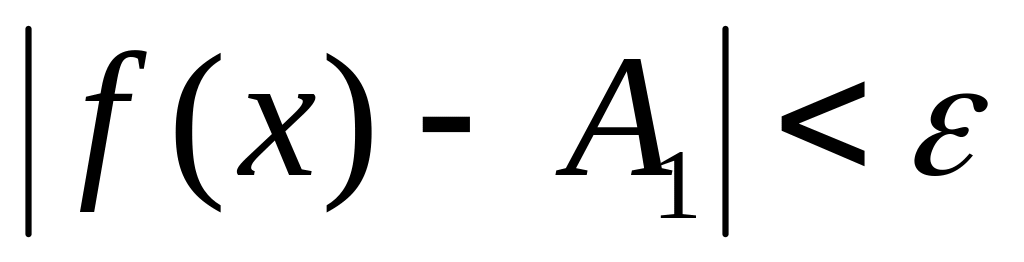 .
.
![]() .
.
3. Предел функции справа запишем с помощью символов:
![]()
![]() .
.
Пределы функции слева и справа называют односторонними пределами
Вычисление пределов функции.
Непосредственное вычисление состоит в том, что вместо аргумента x подставляется его предельное значение, и выполняются все необходимые операции.
Раскрытие неопределенности вида
 состоит в сокращении дроби на множитель,
стремящийся к нулю, при этом, если:
состоит в сокращении дроби на множитель,
стремящийся к нулю, при этом, если:
в числителе и знаменателе дроби многочлены, то их следует разложить на линейные множители
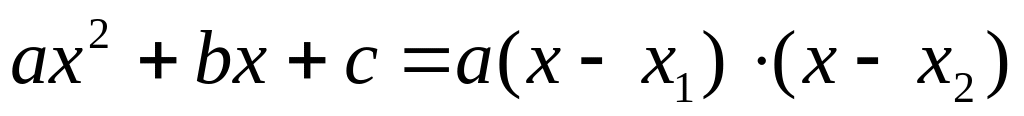 или, если квадратное уравнение приведенное
или, если квадратное уравнение приведенное

под знаком предела иррациональное выражение (выражение, содержащее корень ), то следует числитель и знаменатель умножить на сопряженный множитель [например, для получения формулы (a–b)(a+b)= a2–b2].
под знаком предела находится тригонометрическое выражение, то следует его преобразовать так, чтобы дробь сократилась.
Задача 1.
Вычислить
предел: ![]()
Решение: подставим в дробь, стоящую под знаком предела, x=2:
![]()
Задача 2. Вычислить
предел: ![]()
Решение: при непосредственной подстановке x=4 в дробь, получаем неопределенность вида . Разложим квадратные трехчлены в числителе и в знаменателе на множители.
x2-6x + 8 = 0 По т. Виета
|
x2-5x + 4 = 0 По т. Виета
|
Тогда:
![]() .
.
Задача 3. Найти следующие пределы:
3.1.
a)
![]() ; б)
; б)
![]() ;
;
3.2.
a)
![]() ; б)
; б)
![]() ;
;
3.3.
a)
![]() ; б)
; б)
![]() ;
;
3.4.
a)
![]() ; б)
; б)
![]()
3.5.
a)
![]() ; б)
; б)
![]()
3.6.
a)
![]() ; б)
; б)
![]()
3.7.
a)
![]() ; б)
; б)
![]()
3.8.
a)
![]() ; б)
; б)
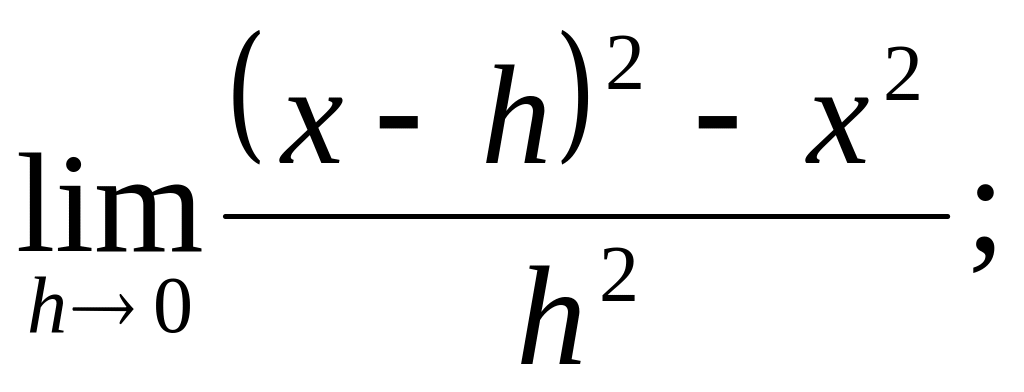
3.9.
a)
![]() ;
б)
;
б)
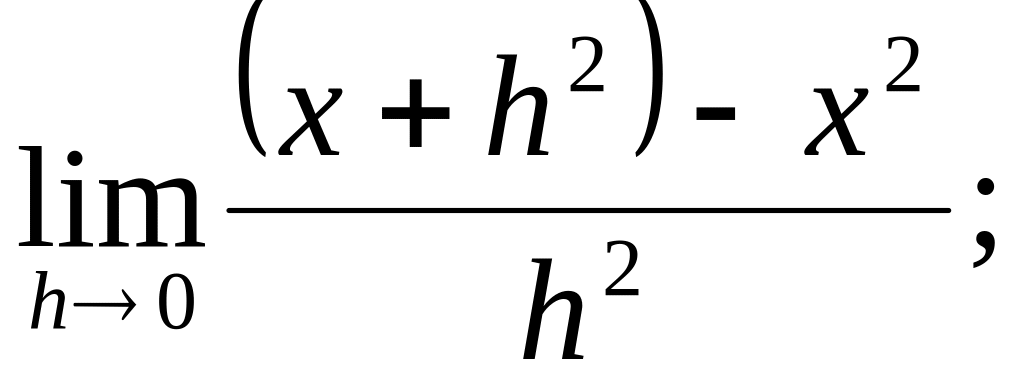
3.10.
a)
![]() ; б)
; б)
![]()
Практическое занятие №4
Первый замечательный предел
Предел вида
![]() называется
первым замечательным пределом.
называется
первым замечательным пределом.
Следствия:
1.![]() ,
2.
,
2.
![]() ,
3.
,
3.![]() ,
,
4.
![]() ,
5.
,
5.
![]() ,
6.
,
6.
![]() ,
,
7.
![]() .
.
Задача 1. Вычислить
предел: ![]()
Решение:
При
непосредственной подстановке имеем
неопределенность вида
![]() .
Преобразуем дробь, стоящую под знаком
предела так, чтобы задача была сведена
к первому замечательному пределу:
.
Преобразуем дробь, стоящую под знаком
предела так, чтобы задача была сведена
к первому замечательному пределу:
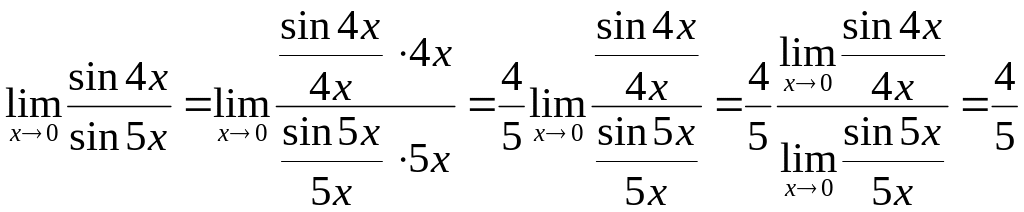
[т.к. и числитель, и знаменатель полученной дроби представляет собой первый замечательный предел].
Задача 2.
2.1.
a)
![]() ; б)
; б)
![]() ;
;
2.2.
a)
![]() ; б)
; б)
![]() ;
;
2.3.
a)
![]() ; б)
; б)
![]() ;
;
2.4.
a)
![]() ; б)
; б)
![]() ;
;
2.5.
a)
![]() ;
б)
;
б)
![]() ;
;
2.6.
a)
![]() ; б)
; б)
![]() ;
;
2.7.
a)
![]() ; б)
; б)
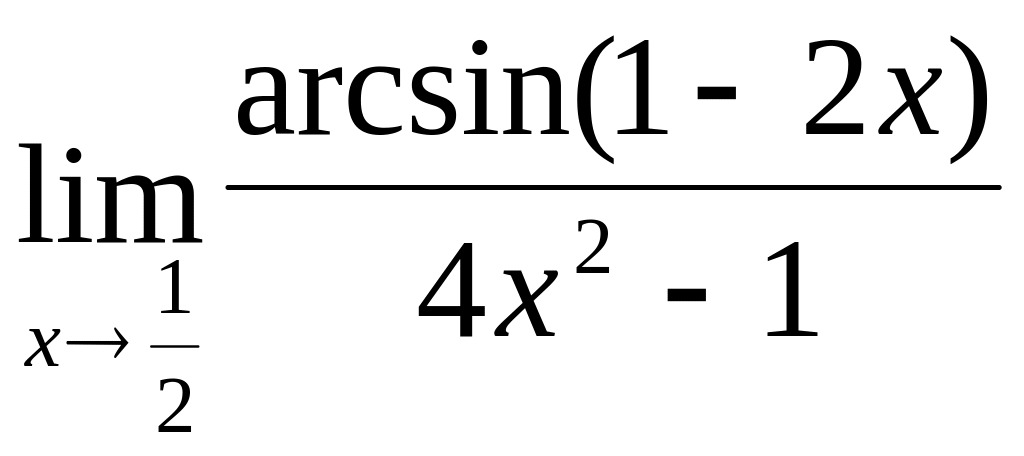 ;
;
2.8.
a)
![]() ; б)
; б)
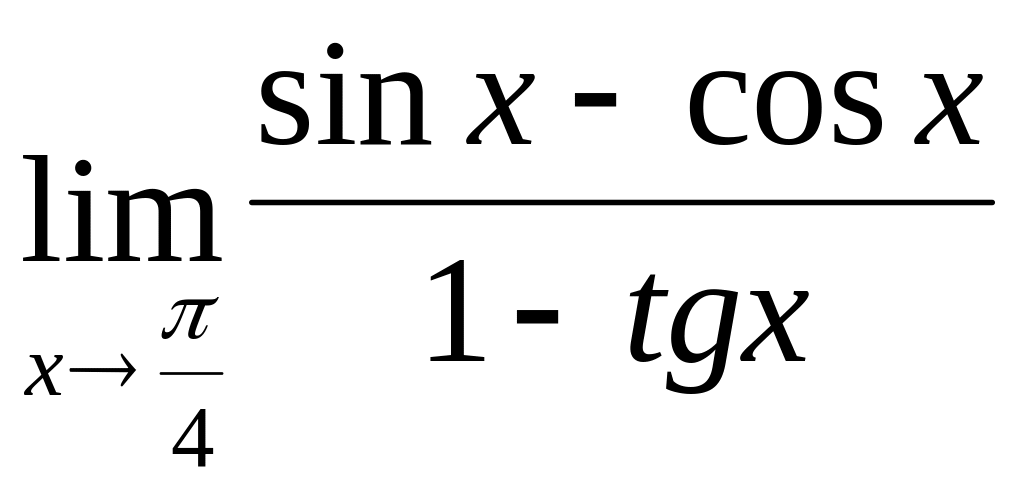 ;
;
2.9.
a)
![]() ;
б)
;
б)
![]() ;
;
2.10.
a)
![]() ; б)
; б)
![]() ;
;
2.11.
a)
![]() ; б)
; б)
![]() ;
;
Практическое занятие № 5,6
Непрерывность функции в точке. Локальные свойства непрерывной функции. Точки разрыва. Глобальные свойства непрерывных функций
