Мультимедиа технология

Вицентий А.В.

Классификация и области применения мультимедиа приложений.

Мультимедиа - совокупность компьютерных технологий, одновременно использующих несколько информационных сред: графику, текст, видео, фотографию, анимацию, звуковые эффекты, высококачественное звуковое сопровождение. Это взаимодействие текста и аудио-эффектов интерактивного программного обеспечения.

Цель – создать продукт, содержащий коллекции изображений, текстов и данных, сопровождающиеся звуком, анимацией, видео и др. визуальными эффектами, включающие интерфейс и др. механизмы управления.

3 принципа:

1. Представление информации с помощью комбинаций множества воспринимаемых человеком сред.

2. Наличие нескольких сюжетных линий в содержании продукта.

3. Интерактивный графический интерфейс и средства навигации.

Технологию мультимедиа составляют специальные аппаратные и программные средства.

Аппаратные средства мультимедиа:

• основные средства: компьютер с высокопроизводительным процессором и памятью большого объема, манипуляторами и мультимедиа-монитором со встроенными стереодинамиками;

• специальные средства: приводы CD-ROM, TV-тюнеры и фрейм-грабберы, графические ускорители, платы видеовоспроизведения, звуковые платы, акустические системы и др.

Основные особенности мультимедиа являются:

1. возможность хранения большого объема разнородной информации на одном носителе.

2. возможность увеличения изображения или его фрагментов без потери качества, возможность сравнения изображений и обработки из разнообразными программными средствами.

3. возможность осуществления аудио-сопровождения соответственно визуальному ряду, возможность использования видеофрагментов.

4. возможность включения БД, возможность подключения к глобальной сети

5. возможность работы с различными приложениями (текстовые, графические, звуковые редакторы)

6. возможность создания собственных галерей, закладок

7. возможность автоматического просмотра всего содержания продукта

8. возможность свободной навигации информации и выхода в основное меню в любой точке продукта.

Классификация мультимедийных систем в сфере применения:

1. Образовательные программы

   1. Тренировочные и Обучающие

   2. Системы поиска информации

   3. Инструментальные средства познавательного и креативного характера

   4. Инструментальные средства для обеспечения коммуникаций

   5. Моделирование программы

«+» внимание удваивается, экономия времени 30%, знания сохраняются дольше

Факторы:

Лучшее, более глубокое понимание изучаемого материала

Мотивация обучаемого на контакт с новой областью знаний

Экономия времени

Знания быстрее восстанавливаются после краткого повторения

Уменьшение затрат на обучение и повышение квалификации

«-» раскрытие коммерческой информации, при более глубокой переработке материала эффективность падает, нет дискуссий и вопросов

2 Бизнес-приложения

2.1 Бизнес-презентации

2.2 РОS (pointer of save) – точки продажи (терминалы).

2.3 Системы торговли (интернет-магазины).

2.4 Программы демонстрации и подбора товара

Витринная реклама. Клиент имеет возможность самостоятельно получать информацию. Н-р, система продажи ж/д билетов или выбор товаров

«+» быстрая реакция на запрос, возможность получения статистической информации, об отношении покупателя к покупке и информации по спросу в данной области рынка.

3 Мультимедиа для моделирования

3.1 В военной сфере - от систем обучения пилотов, до мультимедиа программ проигрывания различных сценариев сражений (+: нет жертв, нет ущерба экологии).

3.2 В гражданской сфере – те же пилоты, программы моделирования и управления трафиком (автомобильным, ж.д., авиа-трафиком, и т.д.) Н-р, датчики для светофоров.

3.3 В научных исследованиях

3.4 Кибер – пространство (виртуальная реальность)

4 В сфере развлечений

4.1 Компьютерные игры

4.2 Видео и звук сопровождающий изображение

4.3 Видео чат

Кабинные симуляторы (автомобили, аттракционы).

Теория информационных процессов и систем

Быстров В.В.

Нечеткие множества: основные понятия, базовые операции.

Лютфи Аскер Заде – основатель нечетких множеств и нечеткой логики.

Нечетким множеством Ã на множестве X называется совокупность пар

à = { μA(X), X }

где

μA(X) – функция принадлежности нечеткого множества Ã,

X – носитель нечеткого множества Ã

Есть разные способы задания нечетких множеств:

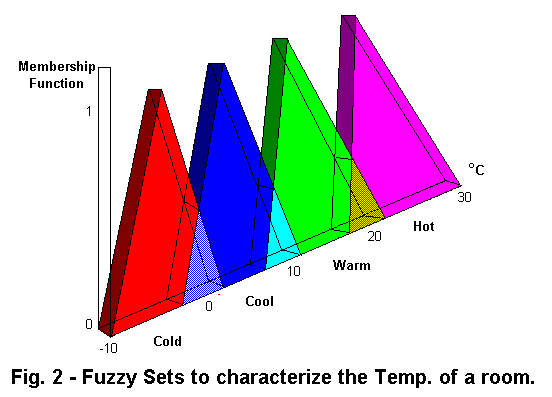
V = {A1; A2; A3; A4}

A1 = «холодно»

A2 = «прохладно»

A3 = «тепло»

A4 = «жарко»

Возраст = {молодой; не молодой}

Имя	Возраст	Степень молодости
Иван	10	1.00
Евгений	21	0.90
Сергей	25	0.5
Анна	26	0.40
Виктор	28	0.20
Роман	83	0.00

[Чтобы принять решение – используется фильтрация.]

Нечеткие числа (трапеции)

à = (m , m , α , β)

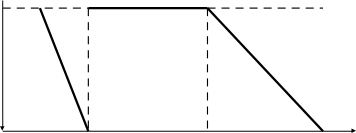
Лингвистическая переменная – переменная, которая может принимать нечеткие значения.

Операции над нечеткими множествами

A = Ã1 (+) Ã2

m = m1 + m2 , m = m1 + m2

α = α1 + α2 , β = β1 + β2

A = Ã1 (-) Ã2

m = m1 – m2 , m = m1 – m2

α = α1 + β 2 , β = β1 + α 2

Доп.вопр.: трапеция проще, треугольник – это частный случай; с помощью трапеции можем задать теругольник.

Случайные числа – например зар.плата – не знаем конкретную сумму.

Почему мы берем трапецию? Т.к. все берется из статистики. Можно подсчитать дисперсию. Для упрощения расчетов.

Основные принципы моделирования (виды подобия), классификация моделей.

Модель – объект-заменитель, который в определенных условиях может заменить объект-оригинал, воспроизводя интересующие свойства и характеристики оригинала, причем имеет существенные преимущества (наглядность, обозримость, доступность испытаний, легкость оперирования и т.д.)

Цель – модель желаемого состояния

Модель определена, если определены следующие понятия:

1. Задача (цель), для которой проводится моделирование.

2. Объект - оригинал, который моделируется.

3. Моделирующий субъект.

4. Средства, из которых создается модель.

5. Среда, в которой модель должна функционировать.

Классификация:

1)По отношению модели к оригиналу в процессе деятельности.

a)Познавательные – форма организации и представления знаний, средство соединения новых знаний с имеющимися. При обнаружении расхождений корректируется модель (горы Хибины и карта)

б)Прагматические – средство управления, способ представления результата (рабочее представление цели) При обнаружении расхождений корректируется оригинал (чертеж дома и дом)

2)[Соотношение типов модели с типами цели]

a) Статические (Структурные схемы систем) – модели конкретного состояния

б) Динамические (Функциональные модели систем) – модели процесса изменения состояния

3)По способу реализации

а) Идеальные конструкции, построенные средствами мышления - абстрактные.

б) Материальные конструкции, построенные средствами реального мира - физические.

в)Особое место (между абстрактными и физическими моделями) занимают языковые (знаковые) модели – физические модели, имеющие абстрактное содержание.(собака)

Физические модели – 3 вида подобия:

-прямое [устанавливается в результате физического взаимодействия в процессе создания модели (след на снегу)]

-косвенное [объективно существует в природе и устанавливается в результате совпадения или близости абстрактных моделей (законов) невесомость - вода]

-условное [устанавливается в результате соглашения (паспорт, любая шифровка)]

Абстрактные модели (идеальные конструкции, построенные средствами мышления):

• Гносеологические( направлены на изучение объективных законов природы – глобус, модель атома);

• Информационные (описывают поведение (не копируют) – инструкция по использованию);

• Сенсуальные (чувственные – живопись, музыка);

• Концептуальные (Причинно-следственные связи, существенные в рамках определенного исследования – курица<->яйцо);

• Математические

  • Аналитические (реализованные на языке математического анализа – (дифференциальные уравнения))

  • Численные (Конечная последовательность действий над числами (разностные уравнения) )

• Имитационные (Моделирование содержательного описания объектов в виде алгоритмов (симуляция состояния – поединок с медведем))

• Статистические (Для оценки скалярной величины a задается случайная величина (кривая – интерполяция(сглаживание точек), экстраполяция (прогноз)))

Основное свойство всех моделей заключается в том, что она принципиально беднее оригинала.

Доп.вопросы: Когда возникло моделирование? – Когда появилась целесообразная деятельность, тогда появилась необходимость моделировать.

Какие св-ва нам интересны? – Зависит от цели (яблоко).

Система (понятие, определение, классификация, большие и сложные системы).

Система – совокупность элементов, объединенных общей функциональной средой и целью функционирования.

Система – устойчивая в пространстве и времени совокупность элементов, решающая определенные задачи. Причем ни один элемент не обладает всеми свойствами системы.

[Системный подход – направление в методологии специального научного познания, в основе которого лежит исследование объектов как систем.

Системотехника – направление в кибернетике, изучающее вопросы планирования, проектирования, конструирования и поведения сложных информационных систем.]

Функциональная среда системы – характерная для системы совокупность законов, алгоритмов и параметров, по которым осуществляется взаимодействие (обмен) между элементами системы и функционирование (развитие) системы в целом.(Самолет в небе – законы физики)

Элемент системы(с точки зрения цели)– условно неделимая, самостоятельно функционирующая часть системы (Дом и водосточная труба)

Компонент системы (подсистема) – множество относительно однородных элементов, объединенных общими функциями при обеспечении выполнения общих целей функционирования и развития системы.(Машина - двигатель)

Структура системы – совокупность связей, по которым обеспечивается энерго-, массо- и информационный обмен между элементами системы, определяющая функционирование системы в целом и способы ее взаимодействия с внешней средой. (акустика в машине - энерго,массо – канализация,информ. – комп.сеть)

[Морфология системы – зафиксированная в пространстве, наблюдаемая, физически реализованная совокупность звеньев структуры системы.]

Категория цели определяет:

• структуру системы;

• функциональную среду системы

Эмерджентность (emergence) – свойство присущее системе, которым не обладает ни одна из ее частей.

СИСТЕМЫ

• Сложные (неоднородность элементов системы) (моделирование которой затруднено из-за недостатка информации о ее функционировании);

• простые;

В сложных системах сущ. Две связи обратная положительная и обратн.отриц.

• Большие (моделирование которой затруднено из-за необходимости рассматривать большое количество элементов и связей между ними);

• малые;

Характерные особенности сложных систем:

1. уникальность;

2. недостаток теоретических и фактических знаний о системе;

3. составной характер системы (система состоит из подсистем);

4. разнородность подсистем и элементов, составляющих систему;

5. случайность и неопределенность факторов, действующих в системе (Пр. счет в банке);

6. многокритериальность оценок процессов, протекающих в системе;

7. большая размерность.

Чем система сложнее, тем > модель зависит от моделирующего subj и цели моделирования. При моделировании сложной системы не обходятся одной моделью, строится ансамбль моделей.

Существенно влияние на формирование сложных систем оказывают цели моделирования и взгляд моделирующего.

Теория сложности: динамическая и комбинаторная сложность:

Комбинаторная сложность – сложность, возникающая из-за необходимости рассмотрения большого числа элементов и комбинаций между элементами.

Динамическая – сложность, возникающая в системе из-за композиций обратных связей (с задержками), т.к. обратные связи м. б. многократны и нелинейны.

Доп.вопросы: Пример эмерджентности, как определение эмерджентности может присутствовать в определении системы? – Не один элемент системы не обладает св-вами целой системы.

Основная задача теории информации. Теорема отсчетов.

ТИ возникла в 1948 г.

Основная задача Т.И. – создание систем связи, обеспечивающих заданную точность при минимальных значениях следующих параметров систем: мощность, полоса частот, время передачи и т.п.

ТИ возникла как теория кодирования и передачи информации.

Информация – отражение реального мира, всеобщее свойство материи (философское определение).

Сигнал – то что обеспечивает взаимодействие объектов.

Сигнал – это материальный носитель информации в пространстве и времени. Следствие изменения состояния obj реального времени. Сигналы могут быть световые (зрительные), слуховые, электромагнитные и др. Сигнал – то, что обеспечивает взаимодействие объектов.

Любой сигнал непрерывен, т.к. любой объект меняет свое состояние.

Возникла необходимость представить сигнал дискретно.

[С точки зрения положения во времени и пространстве сигналы бывают:

1. статические – отражают устойчивое состояние объекта;

2. динамические – отражают непрерывное изменение состояния объектов или процессов при переходе из одного устойчивого состояния в другое. Пр.: любой волновые процессы.

По структуре сигналы делятся на:

1. непрерывные – если сигнал в конечном интервале амплитуд принимает произвольное количество значений.

2. дискретные – сигналы, принимающие ограниченное количество значений.

• Код – правило, по j происходит изменение состояния obj реального мира при передачи инф-ции.

• Кодирование – построение элементов сообщения по определенному закону; преобразование сообщений в сигнал.

• Модуляция – вид воздействия на элементы сообщения с целью преобразования кода в сигнал.]

<При дискретизации возникает проблема адекватности сигнала.>

При дискретном представлении непрерывного сигнала случайная величина может служить мат. моделью сигнала. Это дает возможность использовать теорию вероятностей в качестве мат. аппарата теории инф-ции.

Дискретные сигналы как средство передачи информации нашли более широкое применение, чем непрерывные. Это объясняется тем, что дискретные сигналы в меньшей степени подвержены искажениям под действием помех в каналах связи; искажение дискретного сигнала легче обнаружить, чем искажение непрерывного сигнала и, главное, дискретные сигналы легко обрабатываются ЭВМ и легко отображаются устройствами цифровой индикации.

Теорема Котельникова отвечает на вопрос, каким должен быть выбран интервал отсчетов чтобы непрерывную функцию можно было передать при помощи дискретных сигналов.

Т.И. можно применять для исследования непрерывных сигналов. Исследование непрерывных сигналов в Т.И. начинается с доказательства математической теоремы, которая называется теоремой отсчетов.

[Теорема отсчетов: непрерывный сигнал можно полностью отобразить и точно воссоздать по последовательности измерений, или отсчетов величины этого сигнала, взятых через равные промежутки времени. Отсчеты следует брать через интервалы времени, меньшие или равные половине периода наивысшей частоты, имеющейся в сигнале.]

Согласно теореме Котельникова: если ф-ция непрерывна и частотный спектр ее не содержит составляющих с частотой, превышающей частоту F, то она полностью определяется совокупностью ординат, стоящих друг от друга на расстоянии 1/2F сек.

<Герц – колебания в секунду. Т.Котельникова – интервал в виде дискретных точек >

Доп.вопр.: что дает т.Котельникова?

В качестве мат.моделей сигналов можно использовать случайную величину (цифровое …)

- сжимаем информацию при передаче, меньше помехи, искажение легче обнаружить, пропускная способность дискретных сигналов выше.

Количественная оценка информации. Формула Хартли, формула Шеннона.

Основная задача Т.И. – создание систем связи, обеспечивающих заданную точность при минимальных значениях следующих параметров систем: мощность, полоса частот, время передачи и т.п. Отсюда вытекают 2 технические проблемы: 1.изыскание способов передачи больших объемов инф-и при малых ресурсных, временных, материальных затратах. 2. повышение достоверности принятой инф-и. При повышении достоверности принятой инф-и скорость передачи инф-и уменьшается, а стоимость технич. средств увеличивается. Т.о., возникает необходимость количественного определения инф-и, которая может передаваться по каналам связи с заданной достоверностью. [Количество инф-и, которое несет в себе сообщение, возрастает при увеличении кол-а неопределенности относительно того, какое сообщение из всех возможных будет выбрано. 1 из 10 возможных сообщений несет в себе меньшее кол-во инф-и, чем 1 из 1000000.]

В виде единицы информации принято использовать бит.

Мера информации – то, что может измерить информацию.

Бит – кол-во инф-ии, кот. необходимо, чтобы сообщить, что было выбрано одно из двух равновероятных событий. (Двоичный код – 1 или 0). Если кол-во бит =1, то I=1*log 2=1 бит.

Пример равновероятных событий – подбрасывание монетки.

Алфавит из 2х элементов: m=2 (кол-во символов алфавита).

Передается один элемент: n=1 (кол-во элементов сообщения).

Число различных сообщений: N; N=m^n

Заслуга Хартли в том, что он впервые предложил логарифмическую меру количества информации.

I=log (N)=log (mⁿ)

Log зависит от того, в чем мы будем измерять информацию (в битах – двоичный log).

Если символы неравновероятны, то мы не можем использовать эти формулы. Шеннон предложил формулу с учетом вероятностей характеристик. Формула Шеннона для неравновероятных символов:

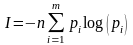
(- , так как вероятность (0,1)) где p_i- вероятность выбора символа s. Она учитывает вероятность появления каждого символа. След-но, p_i будет меньше нуля, а кол-во инф-ии не может быть отрицательным)

В случае равновероятных символов она переходит в формулу Хартли

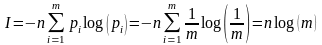
Доп.вопрос:

Может ли инф-ия быть меньше 1 бита?

Теоретически инф-ия м.б. < 1 бит (0-вер-ть одного события, 1 – вер-ть другого). Инф-я = 1бит для равновероятностных ответов, в ост. случаях она меньше 1 бита.

Как это связано с основной задачей теории информации? Для чего это надо?

Нужно измерять задачу количественно. Измерение кол-ва инф-ии – частная задача. Решение частных задач приводит к решению общих задач.

Теоретические основы автоматизированного управления

Малыгина С.Н.

Понятие автоматического и автоматизированного управления. Классификация систем автоматизированного управления.

Управление — действие субъекта, направленное на изменение и манипуляцию объектами и субъектами реальности по заранее продуманной программе.

Теория автоматического управления (ТАУ) — дисциплина, изучающая процессы автоматического управления объектами разной физической природы. При этом при помощи математических средств выявляются свойства систем автоматического управления и разрабатываются рекомендации по их проектированию.

Автоматическое управление – процесс управления происходит без вмешательства человека – автоматически.

Со временем объект управления стал сложным и на смену САУ пришли АСУ.

Автоматизированное управление – человек участвует в процессе управления как элемент системы управления (выбор управляющего воздействия, принятие решения об указании управляющего воздействия.)

Автоматизированная система управления или АСУ — комплекс аппаратных и программных средств, предназначенный для управления различными процессами в рамках технологического процесса, производства, предприятия. АСУ применяются в различных отраслях промышленности, энергетике, транспорте и т. п. Термин автоматизированная, в отличие от термина автоматическая подчеркивает сохранение за человеком-оператором некоторых функций, либо наиболее общего, целеполагающего характера, либо не поддающихся автоматизации.

Автоматизированная система управления технологическим процессом — решает задачи оперативного управления и контроля техническими объектами в промышленности, энергетике и т.п.

Автоматизированная система управления производством — решает задачи организации производства, включая основные производственные процессы, входящую и исходящую логистику. Осуществляет краткосрочное планирование выпуска с учетом производственных мощностей, анализ качества продукции, моделирование производственного процесса.

Автоматизированная система управления предприятием — Для решения этих задач применяются ERP-системы. В случае, если предприятием является высшее учебное заведение, имеет место АСУ ВУЗ.

ERP-система (англ. Enterprise Resource Planning System — Система планирования ресурсов предприятия) — корпоративная информационная система (КИС), предназначенная для автоматизации учета и управления. Как правило, ERP-системы строятся по модульному принципу и охватывают все ключевые процессы деятельности компании.

Корпоративная информационная система — управленческая идеология, объединяющая бизнес-стратегию и информационные технологии.

Корпоративная информационная система — масштабируемая система, предназначенная для комплексной автоматизации всех видов хозяйственной деятельности больших и средних предприятий, в том числе корпораций, состоящих из группы компаний, требующих единого управления.

Корпоративной Информационной Системой может считаться система, автоматизирующая более 80 % подразделений предприятия.

Корпоративные информационные системы ориентированы на крупные компании и могут поддерживать территориально разнесенные узлы или сети. В основном они имеют иерархическую структуру из нескольких уровней.

Функциональная схема АСУ

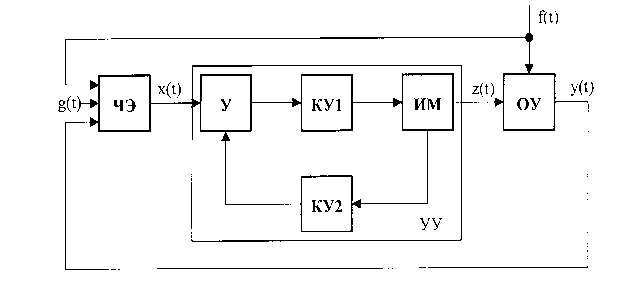
Доп.Вопрос от Горохова: Каким образом человек может влиять на САУ И АСУ? Человек принимает решение об указании управляющего воздействия, выбирает его и через УУ оказывает управляющее воздействие.

Системное ПО

Ломов П.А.

Основные этапы компиляции программ.

Транслятор – это программа, которая переводит входную программу на исходном (входном) языке в эквивалентную ей программу на результирующем (выходном) языке.

К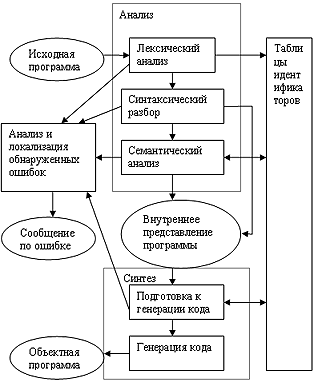 омпилятор (К) – это транслятор, который осуществляет перевод исходной программы в эквивалентную ей объектную программу на языке машинных команд или на языке ассемблера. Выход – obj-ный код (нет привязки к конкр. обл-м памяти)

Процесс компиляции состоит из двух основных этапов – синтеза и анализа.

Анализ - вып-ся распоз-ние текста исх проги (выдел. лексемы), созд-е и запол-ние таблиц идент-ров. Рез-том его работы служит некое внутр представление проги, понятное К.

Синтез - на основании внутр представления проги и инфы, содер-ся в таблице (таблицах) идент-ров, порождается текст рез-щей проги. Рез-том этого этапа явл-ся объектный код. Также, в составе К присутствует часть, ответственная за ан-з и исправление ошибок, кот при наличии ошибки в тексте исх проги д/ макс-но полно инф-ть польз-ля о типе ошибки и месте ее возникновения. В лучшем случае К м/ предложить польз-лю вариант исправления ошибки.

Эти этапы состоят из более мелких этапов, наз-мых фазами компиляции. К в целом с точки зрения теории формальных языков вып-ет 2 основные функции.

1) он является распоз-лем для языка исх проги. Т.е. он д/ получить на вход цепочку символов вх. языка, проверить ее принадлежность к языку и выявить правила, по кот эта цепочка была построена.

2) К явл-ся генератором для языка рез-щей проги. Он д/ построить на выходе цепочку вых. языка по опред. правилам, предполагаемым языком маш. команд или языком ассемблера. Распоз-лем этой цепочки б/ выступать уже выч-ная с-ма, под кот. создается рез-щая программа.

Лексический анализ (сканер) – это часть К, кот. читает литеры проги на исх. языке и строит из них слова (лексемы) исх. языка. На вход лексического анализ-ра поступает текст исх. проги, а вых инфа передается для дальнейшей обр-ки К на этапе синтаксического разбора. С теоретической т. Зр. лексический анализатор не явл-ся обязательной частью К.

Синтаксический разбор – это осн. часть К на этапе ан-за. Она выполняет выделение синтакс-х конструкций в тексте исх. проги, обработанном лексическим анализатором. На этой же фазе компиляции проверяется синтаксическая правильность программы. Синтаксический разбор играет главную роль – роль распознавателя текста вх языка прогр-ния.

Семантический анализ – это часть К, проверяющая правильность текста исх. проги с т. зр. семантики вх. языка. Кроме непосредственно проверки, семантический анализ д/ выполнять преобразование текста, требуемые семантикой вх. языка (такие, как добавление функций неявного преобразования типов). В разл-х реализациях К семантический анализ м/ частично входить в фазу синтаксического разбора, частично – в фазу подготовки к генерации кода.

Подготовка к генерации кода – это фаза, на кот. К выполняются предварительные действия. Непосредственно связанные с синтезом текста рез-щей проги, но еще не ведущие к порождению текста на вых. языке. Обычно в эту фазу входят действия, связанные с идентификацией эл-тов языка, распределением памяти и т.п.

Генерация кода – это фаза, непосредственно связанная с порождением команд, составляющих предложения вых языка и в целом текст рез-щей проги. Это осн. фаза на этапе синтеза рез-щей проги. Кроме непосредственного порождения текста рез-щей проги, генерация обычно включает в себя также оптимизацию – процесс, связанный с обработкой порожденного текста. Иногда оптимизацию выделяют в отдельную фазу компиляции, т.к. она оказывает существенное влияние на качество и эффективность результирующей программы.

Таблицы идентификаторов – это спец образом орг-ные наборы данных, служащие для хранения инфы об эл-тах исх проги, кот

затем исп-тся для порождения текста рез-щей проги. Таблица идентификаторов в конкретной реализации К м/б одна, или же таких таблиц может быть несколько. Элементами исх проги, информацию о кот нужно хранить в процессе компиляции, являются переменные, константы, функции и т.п. – конкретный состав набора элементов зависит от используемого вх ЯП. Понятие «таблицы» вовсе не предполагает, что это хранилище данных должно быть организованно именно в виде таблиц или других массивов информации.

Проход – процесс посл-ного чтения К данных из внеш памяти, их обр-ки и помещения рез-та работы во внеш память. Чаще всего 1 проход вкл. в себя выполнение 1 или неск-х фаз компиляции. Рез-том промежуточных проходов явл-ся внутр представление исх проги, рез-том последнего прохода – рез-щая объектная прога. Реальные К, как правило, выполняют от 2 до 5 проходов.

Способы задания формальных языков. Классификация грамматик по Хомскому.

Алфавит – это счетное множество допустимых символов языка.(множество символов V).

Цепочка символов α является цепочкой над алфавитом V: α (V), если в нее входят символы, принадлежащие множеству символов V

Если V – некоторый алфавит, то:

V⁺ - множество всех цепочек над алфавитом V без λ;

V* - множество всех цепочек над алфавитом V включая λ.

Языком L над алфавитом V: L(V) называется некоторое счетное подмножество цепочек конечной длины из множества всех цепочек над алфавитом V.

Способы задания языков.

Итак, каждый язык – это множество цепочек символов над некоторым алфавитом. Но Язык можно задать тремя способами:

1. Перечислением всех допустимых цепочек языка.

2. Указанием способа порождения цепочек языка (заданием грамматики языка).

3. Определением метода распознавания цепочек языка.

Первый из методов является чисто формальным и на практике не применяется, так как большинство языков содержит бесконечное число допустимых цепочек и перечислить их просто невозможно

Второй способ предусматривает некоторое описание правил, с помощью которых строятся цепочки языка. Тогда любая цепочка, построенная с помощью этих правил из символов алфавита, будет принадлежать заданному языку.

Третий способ предусматривает построение некоторого логического устройства (распознавателя) – автомата, который на входе получает цепочку символов, а на выходе выдает ответ: принадлежит или нет эта цепочка заданному языку. Например (односторонние и 2- сторонние головки, детерминир. (для каждой допустимой конструкции сущ. ! 1 к-ция, в j. перейдет распознаватель на след. шаге) и не-, )

Грамматика – описание способа построения предложений некоторого языка. Формальные грамматики классифицируются по структуре их правил. Если все без исключения правила грамматики удовлетворяют некоторой заданной структуре, то ее относят к определенному типу. Форма Бэкуса-Наура (грамматика определяется как 4ка): G(VT,VN,P,S), где VT - мн-во терм. симв, из них строятся результир. конструк-и языка; VN - мн-во не терм. симв (промеж. алф-т); P - система правил (продукций); S - целевой символ. V=VTυVN – полный алфавит грамматики (объединенние).

Классификация грамматик по Хомскому.

Тип 0: грамматики с фразовой структурой.

На структуру их правил не накладывается никаких ограничений: для грамматики вида G(VT,VN,P,S), VN – мн-во нетерм. симв. VT – мн-во терм. Символов. Из них строятся результир. констр. языка. P- правила имеют вид: α→β, где αЄV⁺, βЄV*., S- целевой символ

Практического применения грамматики, относящиеся только к типу 0, не имеют.

Тип 1: контекстно-зависимые (КЗ) и неукорачивающиеся.

КЗ грамматики имеют правила вида: α₁Aα₂→ α₁βα₂, где α₁, α₂ Є V*, AЄVN, βЄV⁺

значение одного и того же символа может быть различным в зависимости от того, в каком контексте он встречается.

Неукорачивающиеся: α→ β, где α,βЄV⁺, длина β > длины α.

Тип 2: контекстно-свободные (КС) грамматики.

КС грамматики имеют правила вид: A→β, где AЄVN, βЄV⁺.

КС-грамматики широко используются при описании синтаксических конструкций языков программирования. Синтаксис большинства известных языков программирования основан именно на КС-грамматиках.

Тип 3: регулярные грамматики.

К типу регулярных относятся два эквивалентных класса грамматик: леволинейные и праволинейные. Леволинейные грамматики могут иметь правила двух видов: A→Bγ или A→γ, где A,BЄVN, γЄVT*. Праволинейные грамматики: A→γB или A→γ, где A,BЄVN, γЄVT*.

Регулярные грамматики используются при описании простейших конструкций языков программирования: идентификаторов, констант, строк, комментариев и т.д. Эти грамматики исключительно просты и удобны в использовании, поэтому в компиляторах на их основе строятся функции лексического анализа входного языка. Любая регулярная грамматика является КС-грамматикой, но не наоборот. Также очевидно, что любая грамматика может быть отнесена к типу 0. В целом можно сказать, что сложность грамматики обратно пропорциональна тому максимально возможному номеру типа.

Пр: тип 0 - G ({0,1},{A,S},P,S) Правила : S->0A1; 0A->00A1; A-> λ Язык: L(G)={0ⁿ1ⁿ|n>0}

Пр: тип 1 - G ({0,1},{A,S},P,S) Правила: S->0A1|01; 0A->00A1|001

Методы оптимизации

Македонов Р.А.

Классификация оптимизационных задач и способов их решения.( не дай бог кому попадётся!!!)

Задача одномерной оптимизации

Рассмотрим задачу поиска минимума одномерной функции f( ), определенной на интервале  .

Постановка задачи

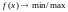
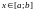
Если функция f( ) определена и дважды непрерывно дифференцируема на интервале [ , ], то необходимыми и достаточными условиями минимума этой функции в точке   являются условия . Точками, в которых функция f( ) принимает наименьшее на интервале   значение, могут быть либо ее стационарные точки, лежащие внутри интервала  , либо ее точки недифференцируемости (критические точки критерия оптимальности), к которым следует отнести также концы интервала  . Поэтому точку, в которой функция f(x) принимает наименьшее на интервале   значение, нужно искать, сравнивая значения этой функции во всех стационарных и критических точках.

Методы решения

а) Классический метод.

Достоинства: простота.

Недостатки: 1) имеет ограниченное применение при решении практических задач (практически не имеет применения!); 2) сложность решения уравнения 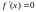- производная может не существовать, описание функции нельзя получить; 3) некоторые уравнения решаются только графически – решение – график (рисунок).

Все остальные методы накладывают ограничения применимости!

б) Прямые методы (не требуют вычисления производных функции).

Достоинства этих методов – функция может быть не задана в аналитическом виде, не требуется вычислять производные функции.

Условия применения – функция должна быть унимодальной. Унимодальной называется функция, имеющая на заданном отрезке [a,b] один максимум или минимум.

Основные представители: метод перебора, метод дихотомии (деления отрезка пополам), метод золотого сечения

Метод перебора или равномерного поиска является простейшим из прямых методов минимизации и состоит в следующем.

Разобьем отрезок [a,b] на n равных частей точками деления:

xi=a+i(b-a)/n, i=0,...n

Вычислив значения F(x) в точках xi, путем сравнения найдем точку xm, где m - это число от 0 до n, такую, что

F(xm) = min F(xi) для всех i от 0 до n.

Погрешность определения точки минимума xm функции F(x) методом перебора не превосходит величены Eps=(b-a)/n.

Деление пополам.

Рассмотрим функцию F, которую требуется минимизировать на интервале [a1, b1]. Предположим, что F строго квазивыпукла. Очевидно, что наименьшее число вычислений значений функции , которые необходимы для сокращения интервала неопределенности, равно двум. Одной из стратегий является выбор этих двух точек симметрично на расстоянии eps>0 от середины интервала. Здесь число eps настолько мало, чтобы длина нового интервала неопределенности eps+(b1-a1)/2 являлась достаточно близкой к теоретическому значению (b1-a1)/2, и в то же время такое, чтобы значение функции в этих двух точках были различимы.

Алгоритм дихотомического поиска Алгоритм дихотомического метода для минимизации строго квазивыпуклой фунции на интервале [a1,b1].

Начальный этап. Выбрать константу различимости 2еps > 0 и допустимую конечную длину интервала неопределенности l > 0. Пусть [a1,b1] - начальный интервал неопределенности. Положить k=1 и перейти к основному этапу.

Основной этап.

Шаг 1. Если bk-ak < l, то остановиться; точка минимума принадлежит интервалу [ak,bk]. В противном случае вычислить pk=(ak+bk)/2-eps qk=(ak+bk)/2+eps и перейти к шагу 2.

Шаг2. Если F(pk) < F(qk), положить a[k+1]=ak и b[k+1]=qk. В противном случае положить a[k+1]=pk и b[k+1]=bk. Заменить k на k+1 и перейти к шагу 1.

Метод золотого сечения

Сравнение различных процедур линейного поиска естественно производить в соответствии со следующим коэффициентом сжатия (длина интервала неопределенности после k выполненных наблюдений)/(длина интервала неопределенности до выполнения наблюдений). Очевидно, что более эффективные схемы соответствуют меньшим значениям коэффициента сжатия. В дихотомическом поиске значение коэффициента приблизительно равно (0.5)^(k/2). Метод золотого сечения является более эффективным, для него значение коэффициента сжатия равно (0.618)^(k-1). Рассмотрим такое симметричное расположение точек x1 и x2 на отрезке [a,b], при котором одна из них становится пробной точкой и на новом отрезке, полученном после исключения части исходного отрезка. Использование таких точек позволяет, кроме первой, ограничиться определением только одного значения f(x), так как другое значение уже найдено на одной из предыдущих итераций. Для определения точек x1 и х2 рассмотрим сначала отрезок [0,1] и для определенности положим, что при уменьшении исключается правая часть этого отрезка. Пусть х2=q, тогда симметрично расположенная точка x1=1-q. Пробная точка х1 отрезка [0,1] перейдет в пробную точку х1'=1-q нового отрезка [1,q]. Чтобы точки x2=q и x2'=1-q делили отрезок и [0,1] и [0,q] в одном и том же отношении, должно выполняться равенство 1/q = q/(1-q) или q^2 = 1-q откуда находим положительное значение q = 0.61803... Таким образом для произвольного отрезка [a,b] выражения для пробных точек примут вид: x1=a+(1-q)(b-a) x2=a+q*(b-a) Алгоритм метода золотого сечения

Алгоритм метода золотого сечения для минимизации строго квазивыпуклой фунции на интервале [a1,b1].

Начальный этап. Выбрать допустимую конечную длину интервала неопределенности l>0. Пусть [a1,b1] - начальный интервал неопределенности. Положить p1=a1+(1-0.618)(b1-a1) и q1=a1+0.618(b1-a1). Вычислить F(p1) и F(q1), положить k=1 и перейти к основному этапу.

Основной этап.

Шаг 1. Если bk-ak < l, то остановиться; точка минимума принадлежит интервалу [ak,bk]. В противном если F(pk)>F(qk), то перейти к шагу 2, а если F(pk)<=F(qk),то к шагу 3. Шаг2. Положить a[k+1]=pk, b[k+1]=bk, p[k+1]=qk, q[k+1]=a[k+1]+0.618(b[k+1]-a[k+1]). Вычислить F(q[k+1]) и перейти к шагу 4. Шаг3. Положить a[k+1]=ak, b[k+1]=qk,q[k+1]=pk, p[k+1]=a[k+1]+(1-0.618)(b[k+1]-a[k+1]). Вычислить F(p[k+1]) и перейти к шагу 4. Шаг4. Заменить k на k+1 и перейти к шагу 1.

Указать хотя бы один недостаток прямых методов – слабая сходимость.

в) Методы, использующие производные функции.

Достоинства – методы этого класса обладают высокой скоростью сходимости вблизи точки оптимума.

Условия применения – функция должна быть выпуклой.

Представитель: метод касательных (метод Ньютона).

Основная идея метода заключается в следующем: задаётся начальное приближение вблизи предположительного корня, после чего строится касательная к исследуемой функции в точке приближения, для которой находится пересечение с осью абсцисс. Эта точка и берётся в качестве следующего приближения. И так далее, пока не будет достигнута необходимая точность.

Пусть   — определённая на отрезке   идифференцируемая на нём вещественнозначная функция. Тогда формула итеративного исчисления приближений может быть выведена следующим образом:

где α — угол наклона касательной в точке  .

Следовательно, искомое выражение для   имеет вид:

Итерационный процесс начинается с некоего начального приближения x₀ (чем ближе к нулю, тем лучше, но если предположения о нахождении решения отсутствуют, методом проб и ошибок можно сузить область возможных значений, применив теорему о промежуточных значениях).

г) Методы оптимизации многомодальных функций.

Достоинства – можно применять и для мультимодальных функций.

Представитель: метод ломанных. Этот прямой метод рассчитан на минимизацию мультимодальных функций, удовлетворяющих условию Липшица. В нем используются кусочно-линейные аппроксимации функции 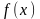, графиками которых являются ломаные.

Условие применения этого метода – функция должна удовлетворять условию Липшица.

Задача безусловной оптимизации функций многих переменных

Постановка задачи

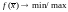
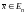, х –вектор из n-мерного пространства (принадлежит всему Эвклидову пространству) без ограничений.

Методы решения

а) Классический метод

Недостатки аналогичны недостаткам классического метода оптимизации функции одной переменной.

Дифференцируемость функции в точке, дифференциал

Пусть функция y = f(x) определена в некоторой окрестности точки x₀. Функция f(x) называется дифференцируемой в точке х₀, если ее приращение представимо в виде

Δf = f(x0 + Δx) − f(x0) = A · Δx + o(Δx) ,

где A — число, не зависящее от Δх, а o(Δx) — функция более высокого порядка малости чем Δx при Δх → 0 .

Таким образом, приращение дифференцируемой функции является суммой линейной относительно Δx ч асти A · Δx и бесконечно малой более высокого порядка малости чем Δx при Δх → 0.

Линейная часть приращения дифференцируемой функции называется дифференциалом в точке х₀ и обозначается символом df(x₀), т.е.

df(x0) = A · Δx.

Необходимое и достаточное условие дифференцируемости

Теорема . Для того, чтобы функция f(x) была дифференцируема в точке x₀, необходимо и достаточно, чтобы в этой точке она имела конечную производную.

Следствие. Функция, дифференцируемая в точке, непрерывна в этой точке.

б) Прямые методы.

Достоинства – не требуют вычисления производных функции, функция не обязательно должна быть задана в аналитическом виде.

Представители: метод случайного поиска, метод случайных направлений, метод случайных направлений с возвратом при неудачном шаге.

Недостаток: плохая сходимость.

в) Методы, использующие производные функции.

Достоинтсва – высокая скорость сходимости по сравнению с прямыми методами.

Представитель: метод градиентного спуска. Градиент показывает направление скорейшего убывания функции.

Задача многомерной оптимизации при наличии ограничений

Постановка задачи

,

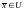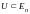
Задачи математического программирования

1) Задача линейного программирования (ЗЛП)

,

Ограничения(равенства и неравенства):

,

,

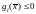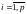
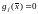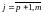
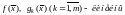
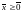
Методы решения

а) Графический метод.

Геометрический метод применяется, если задача линейного программирования содержит только две переменные. Рисуем область допустимых решений и график целевой функции. Сдвигаем график целевой функции параллельным переносом в направлении ее вектора нормали (для задач максимизации) или в противоположном направлении (для задач минимизации). Последняя общая точка сдвинутого графика целевой функции и области допустимых решений и есть решение задачи. Возможно, что график совпадает с одним из отрезков, ограничивающих допустимую область решений. В этом случае решений будет бесконечно много.

Достоинства – простота, наглядность. Недостатки – ограниченность применения.

б) Симплекс-метод.

Симплекс метод или метод последовательного уточнения оценок

 Симплексный метод задач линейного программирования основан на переходе от одного опорного плана к другому, при котором значение целевой функции возрастает (при условии, что данная задача имеет оптимальный план, и каждый ее опорный план является невырожденным). Указанный переход возможен, если известен какой-нибудь исходный опорный план.

Метод предназначен для решения общей задачи линейного программирования.  Пусть имеем следующую задачу:  , с системой ограничений следующего вида: 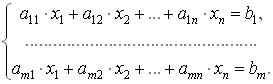 Разрешим эту систему относительно переменных  x₁,...x_m: 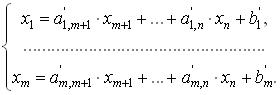(7.3) Векторы условий, соответствующие x₁,...x_m, образуют базис. Переменные x₁,...x_m назовем базисными переменными. Остальные переменные задачи - небазисные. Целевую функцию можно выразить через небазисные переменные: . Если приравнять небазисные переменные нулю  , то соответствующие базисные переменные примут значения  . Вектор    с такими компонентами представляет собой угловую точку многогранника решений (допустимую) при условии, что b_i' ≥ 0 (опорный план). Теперь необходимо перейти к другой угловой точке с меньшим значением целевой функции. Для этого следует выбрать некоторую небазисную переменную и некоторую базисную так, чтобы после того, как мы "поменяем их местами", значение целевой функции уменьшилось. Такой направленный перебор в конце концов приведет нас к решению задачи.

Достоинства – при нескольких модификациях является универсальным методом решения ЗЛП.

в) Двойственный симплекс-метод. Применяется когда исходную задачу сложнее решить, чем двойственную.

2-я теорема двойственности. Компоненты оптимального решения двойственной задачи равны абсолютным значениям коэффициентов

при соответствующих переменных линейной функции исходной задачи, выраженной через неосновные переменные ее оптимального решения. На этой теореме основан двойственный симплекс-метод.

2) Задача нелинейного программирования (ЗНП)

,

,

,

Универсальных методов таких задач не существует. Эффективные алгоритмы удалось разработать лишь для некоторых классов таких задач: задача дробно-линейного программирования, задача квадратичного программирования, задачи с линейной целевой функцией, задачи с линейными ограничениями и т.п.

Можно рассмотреть метод решения задач с линейными ограничениями и нелинейной целевой функцией – метод Франка-Вульфа.

Метод Франка-Вульфа. Ограничения содержат только линейные неравенства. Эта особенность является основой для замены в окрестности исследуемой точки нелинейной целевой функции линейной, в результате чего решение исходной задачи сводится к последовательному решению задач линейного программирования

Численные методы/Вычислительная математика

Малыгина С.Н.

Постановка задач аппроксимации функций одной переменной: Интерполирование алгебраическими многочленами.

Аппроксима́ция, или приближе́ние — научный метод, состоящий в замене одних объектов другими, в том или ином смысле близкими к исходным, но более простыми.

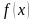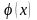В основе большинства численных методов математического анализа лежит подмена одной функции (известной, неизвестной или частично известной) другой функцией , близкой к и обладающей «хорошими» свойствами, позволяющими легко производить над нею те или иные аналитические или вычислительные операции. Такая подмена называется аппроксимацией или просто приближением функции функцией . Такую подмену можно сделать разными способами:

(Допролнительно!)

• Сплайны

Под сплайном (от англ. spline — планка, рейка) обычно понимают кусочно-заданную функцию, совпадающую с функциями более простой природы на каждом элементе разбиения своей области определения. При аппроксимации сплайнами исходную функцию заменяют многочленами на каждом ее кусочке.

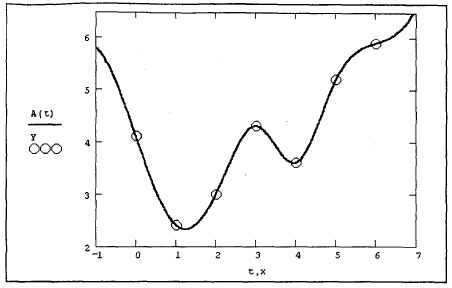
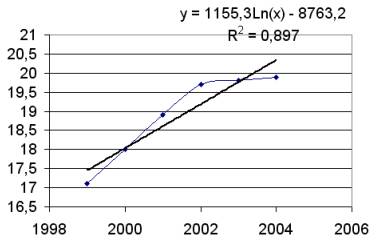
• Аппроксимация эмпирическими функциями

Эмпирические формулы служат для аналитического представления опытных данных. На основе этих данных требуется подобрать функцию y=φ(x), которая наилучшим образом сглаживала бы экспериментальную зависимость между переменными и по возможности точно отражала общую тенденцию зависимости между x и y, исключая погрешности измерений и случайные отклонения.