Семинар 4.

Тема: Непараметрические критерии согласия, однородности и независимости.

Критерии согласия:

при альтернативе

Критерий Колмогорова

-непрерывная функция

- эмпирическая функция распределения

малые выборки 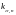из таблиц

большие выборки

квантиль распределения

Критерий

статистика критерия ,

где -число «карманов», число элементов выборки, попавших в -й карман, - теоретическая вероятность попадания в -й карман.

Критическая область

Критерии однородности:

при альтернативе

Критерий Колмогорова- Смирнова

- эмпирические функции распределения

малые выборки из таблиц

большие выборки

Критерий Манна-Уитни-Вилкоксона

Пусть ранги наблюдений в вариационном ряду объединенной выборки . Статистика критерия

Если верна гипотеза то статистика имеет предельное распределение .

Критическая область

Критерии независимости:

против альтернативы

Критерий Спирмена

Пусть ранг в вариационном ряду , ранг в вариационном ряду .

Ранговый коэффициент корреляции Спирмена

Другие формулы для коэффициента корреляции Спирмена

Предельное распределение

Критическая область

Критерий

число элементов выборки таких, что

Статистика критерия

Критическая область

Задача 1. Используя критерий Колмогорова для следующей выборки

2,52

0,09

1,03

1,85

0,31

1,32

0,12

3,01

1,09

1,89

проверить гипотезу о том, что генеральная совокупность имеет экспоненциальное распределение с параметром .

Задача 2. В опытах по селекции гороха Г.И. Медель скрещивал растения с круглыми желтыми семенами и растения с морщинистыми зелеными семенами. В таблице приведены наблюдаемые им частоты эксперимента и теоретические вероятности, которые дает теория наследственности. Используя критерий , проверить гипотезу о согласовании частотных данных с теоретическими вероятностями. Уровень значимости .

Виды семян	Частота	Вероятность
Круглые и желтые	315	9/16
Морщинистые и желтые	101	3/16
Круглые и зеленые	108	3/16
Морщинистые и зеленые	32	1/16

Задача 3. Используя критерий Колмогорова-Смирнова проверить гипотезу против альтернативы по данным из таблицы

Xi	-0,15	8,6	5,0	3,7	4,3	7,7	2,3	3,3	-1,2	8,4
Yj	2,5	12,0	0,5	0,4	2,7	-0,9	1,7	0,7	-0,4	-0,3

Уровень значимости (вероятность ошибки первого рода) принять равным .

Проверить эту же гипотезу с помощью критерия Вилкоксона.

Задача 4. Используя ранговый критерий Спирмена проверить гипотезу независимости против альтернативы по данным из таблицы

Xi	-1,6	1,1	1,2	-1,9	0,4	-1,1	-0,3	0,6	0,1	0,9
Yi	0,5	0,8	-1,2	0,85	-0,6	-0,2	0,1	-0,7	0,79	0,15

Уровень значимости (вероятность ошибки первого рода) принять равным .

Задача 5. В таблице приведены статистические данные о 6800 человек, расклассифицированных по цвету глаз и цвету волос

					Сумма
	1768	807	189	47	2811
	946	1387	746	53	3132
	115	438	288	16	857
Сумма	2829	2632	1223	116	6800

Используя критерий , проверить гипотезу о независимости цвета глаз и цвета волос.

Уровень значимости (вероятность ошибки первого рода) принять равным .

Дома.

Задача 1. В таблице приведена дневная выручка (в тыс. руб.) одного и того же магазина за семь зимних и восемь летних дней.

зима	39	50	61	67	40	40	54	---
лето	60	53	42	41	40	54	63	69

Используя критерий Вилкоксона , ответить на вопрос: можно ли считать, что летом спрос на товары выше, чем зимой? Принять .

Проверить эту же гипотезу с помощью критерия Колмогорова-Смирнова.

Задача 2. В таблице приведены показания 500 часов, выставленных на продажу в витринах часовщиков. Пусть -номер промежутка от -го часа до часа, , -количество часов, показания которых попали в -ый промежуток.

	0	1	2	3	4	5	6	7	8	9	10	11	сумма
	41	34	54	39	49	45	41	33	37	41	47	39	500

Используя критерий , проверить гипотезу о том, что показания часов имеют равномерное распределение. Уровень значимости .

Задача 3. Десять бегунов, упорядоченные по росту, в забеге заняли следующие места

6, 5, 1, 4, 2, 7, 8, 10, 3, 9. Используя критерий Спирмена, проверить гипотезу о независимости роста и скорости бега. Уровень значимости принять равным .

Задача 4. При бросаниях монеты Бюффон наблюдал выпадений «герба» и выпадений «решки». Используя критерий , проверить гипотезу о симметрии монеты. Уровень значимости принять равным .