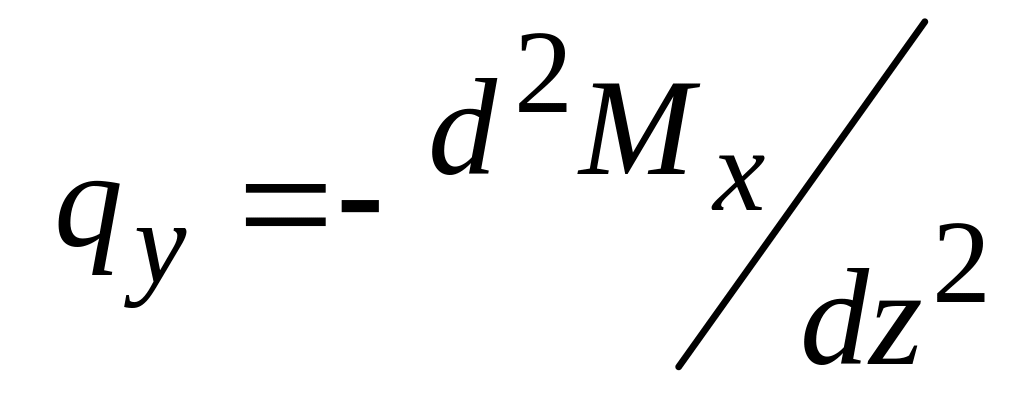2.3 Вопросы и ответы для самоконтроля
1. Чему равен статический момент площади сечения относительно оси.
,
.
Статический момент площади сечения
относительно какой-либо оси равен
произведению площади сечения на
координату ее центра тяжести до этой
оси
2. Чему равен статический момент составного сечения относительно какой-либо оси ?
,
Статический
момент составного сечения относительно
какой-либо оси равен алгебраической
сумме статических моментов типовых
сечений составного сечения относительно
этой же оси.
3. Формулы для определения положения центра тяжести сечения.
, 
Координата центра тяжести сечения
относительно какой-либо оси равна
статическому моменту площади сечения
относительно этой оси деленному на
площадь сечения.
4. Перечислить формулы для определения осевых моментов инерции типовых сечений относительно собственных центральных осей (прямоугольник, прямоугольный треугольник, круг, кольцо).
5. Формулы перехода к параллельным осям для осевых моментов инерции сечения.
,
Осевой момент инерции сечения относительно
оси, параллельной центральной оси
сечения, равен сумме осевого момента
инерции сечения относительно собственной
центральной оси и произведения площади
сечения на квадрат расстояния между
осями
6. Какие оси сечения называются главными центральными осями ?
Оси сечения, относительно которых
осевые моменты инерции имеют экстремальные
значения (
),
а центробежный момент инерции равен
нулю, называются главными центральными
осями.
7. Закон постоянства суммы осевых моментов инерции сечения.
.
Сумма осевых моментов инерции относительно
любых взаимно перпендикулярных
центральных осей сечения равна сумме
главных моментов инерции и есть величина
постоянная , равная полярному моменту
инерции сечения
.
8. Формулы для определения главных моментов инерции сечения.
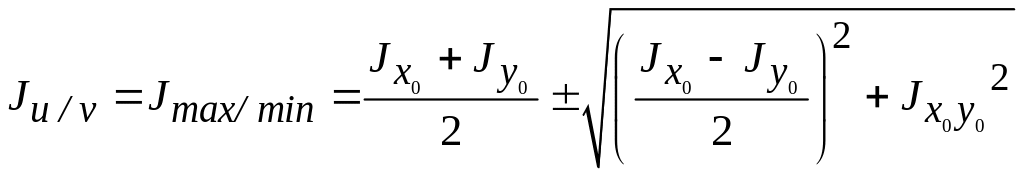
9. Формулы для определения положения главных центральных осей
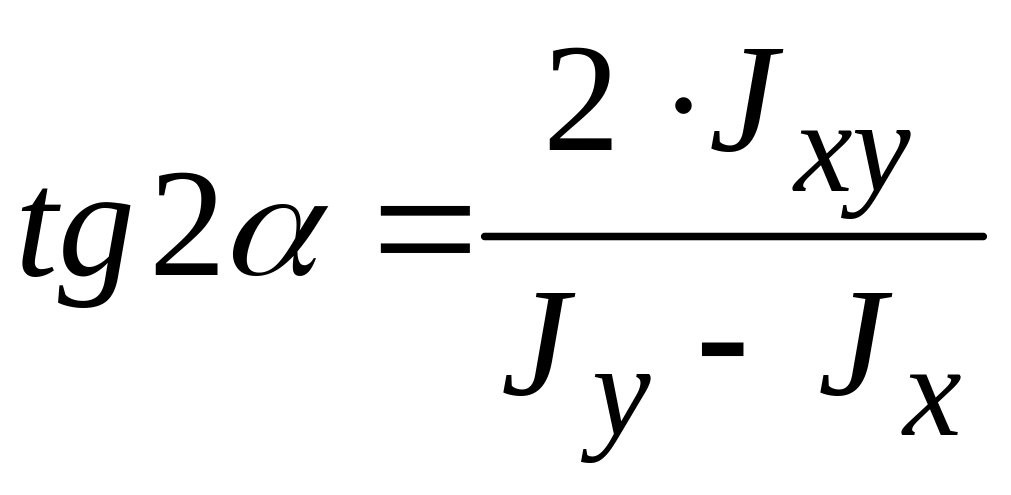или
.
3 Внутренние силовые факторы
3.1 Основные понятия и формулы
Под действием внешних нагрузок происходит деформация элементов конструкции и изменение величин внутренних сил. Для определения величины внутренних сил применяется метод сечений, который заключается в следующем.
Рассечем мысленно элемент конструкции сечением на две части в соответствии с рисунком 3.1
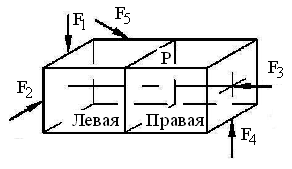
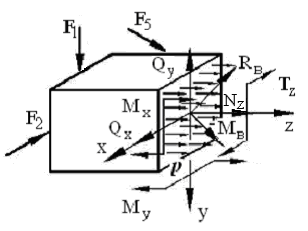
Рисунок 3.1.
2. Отбросим одну правую часть.
3. Заменим действие отброшенной части внутренними силами упругости, распределенными по всему сечению.
Равнодействующий
вектор внутренних сил
,
преложенный в центре тяжести сечения,
называется главным вектором внутренних
сил.
Равнодействующий
момент внутренних сил
,
действующий относительно центра тяжести
сечения, называется главным моментом
внутренних сил. Разложим их на составляющие
по осям подвижной системы координат х,
у,
z,
с началом в центре тяжести сечения.
-
продольная сила равна сумме проекций
всех внутренних сил, действующих в
сечении, на нормаль к сечению.
,
- поперечные силы равны сумме проекций
всех внутренних сил, действующих в
сечении, на поперечные оси сечения у,
х.
,
- изгибающие моменты равны сумме моментов
всех внутренних сил, действующих в
сечении, относительно поперечных осей
х,
у.
-
крутящий момент равен сумме моментов
всех внутренних сил, действующих в
сечении, относительно продольной оси
z.
4. Из уравнений равновесия отсеченной части стержня получаем уравнения для определения внутренних силовых факторов и напряжений.
-
продольная сила в любом сечении равна
алгебраической сумме проекций всех
внешних сил, действующих на отсеченную
часть стержня, на продольную ось z.
,
- поперечные силы в любом сечении равны
алгебраической сумме проекций всех
внешних сил, действующих на отсеченную
часть стержня, на поперечные оси y,
x.
-
крутящий момент в любом сечении равен
алгебраической сумме моментов всех
внешних сил, действующих на отсеченную
часть стержня, относительно оси z.
,
-
изгибающие моменты в любом сечении
равны алгебраической сумме моментов
всех внешних сил, действующих на
отсеченную часть стержня, относительно
осей х, y.
Правило знаков при определении внутренних силовых факторов в соответствии с рисунком 3.2
Проекции внешних продольных сил положительны, если они направлены от рассматриваемого сечения.
Проекции внешних поперечных сил положительны, если они направлены вверх слева от сечения и вниз справа от сечения.
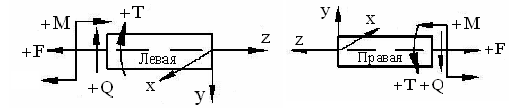
Рисунок 3.2
Крутящий момент от внешних нагрузок положителен, если он действует по часовой стрелке относительно оси z любой отсеченной части стержня.
Изгибающий момент от внешних нагрузок положителен, если он действует по часовой стрелке относительно поперечной оси слева от сечения и против часовой стрелке справа от сечения.
В зависимости от действующих внутренних силовых факторов проводится классификация видов нагружения стержней (состояний стержней). Принято 5 простых видов состояния стержней в соответствии с рисунком 3.3
-
состояние растяжения – сжатия. Если
,
то стержень испытывает растяжение, если
- сжатие.
или
- состояние чистого сдвига;
-
состояние чистого кручения;
или
- состояние чистого изгиба;
и
или
и
- состояние поперечного изгиба.
Рисунок 3.3
При простых состояниях стержней справедлива гипотеза плоских сечений: сечения плоские до деформаций остаются плоскими и перпендикулярными оси стержня и после деформаций.
При составлении уравнений внутренних силовых факторов пользуются прямоугольной системой координат и правилами знаков. При этом внутренние силовые факторы, действующие в сечениях левой отсеченной части, равны внутренним силовым факторам правой отсеченной части, но действуют в противоположных направлениях. Для определения закона их изменения по длине элемента конструкции по уравнениям внутренних силовых факторов строятся графики их изменения, называемые эпюрами внутренних силовых факторов. По этим эпюрам определяется состояние стержня и опасное сечение с максимальным значением силового фактора.
Между интенсивностью внешней распределенной нагрузки и внутренними силовыми факторами, а также между внутренними силовыми факторами существуют дифференциальные зависимости. Рисунок 3.4.
Рисунок 3.4 |
Откуда
|
,
,
