2. Строим эпюры поперечной силы и изгибающего момента

Для участка АВ уравнение прямой

- уравнение квадратной параболы

Для участка ВС

- уравнение прямой

- уравнение квадратной параболы Определяем экстремальное значение изгибающего момента

Отсюда

Тогда .

Определяем выпуклость эпюры изгибающего момента

- выпуклость эпюры вверх

Для участка DC

- уравнение прямой

По найденным значениям строим эпюры поперечной силы и изгибающего момента по всем участкам балки.

3. Определяем опасное сечение. Опасным по максимальным нормальным напряжениям является сечение при с . Максимальное значение поперечной силы в сечении А с .

4. Из условия прочности по максимальным нормальным напряжениям определяем размеры прямоугольного сечения при .

Отсюда

Осевой момент сопротивления прямоугольного сечения . Отсюда см . Принимаем см

Тогда см², см²

Определяем напряжения и строим их эпюры, в соответствии с рисунком 4.15 а.

МПа на 0,375 %

МПа

Определяем коэффициент металлоемкости

3. Определяем диаметр круглого сечения

Осевой момент сопротивления круглого сечения . Отсюда см. Принимаем см.

Тогда см³ см²

Определяем напряжения и строим их эпюры, в соответствии с рисунком 4.15 б.

МПа на 0,5 %

МПа

Определяем коэффициент металлоемкости

4. Определяем размеры кольцевого сечения.

Осевой момент сопротивления кольцевого сечения

Отсюда см

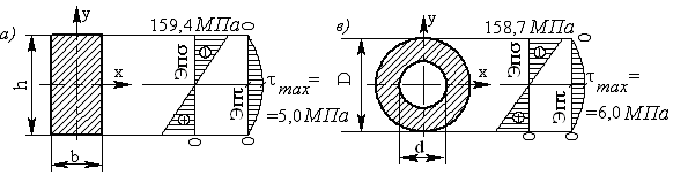
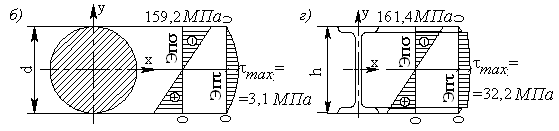
Рисунок 4.15

Принимаем см.

Тогда см³

см²

Определяем напряжения и строим их эпюры, в соответствии с рисунком 4.15 в

МПа на 0,18 %

МПа

Определяем коэффициент металлоемкости

5. Подбираем сечение двутавра. По сортаменту подбирается двутавр №24 см, см, см, , см²,

см⁴, см³ , см³.

Определяем напряжения и строим их эпюры, в соответствии с рисунком 4.15 г.

МПа на 1,90 %

МПа

Определяем коэффициент металлоемкости

Таким образом, наиболее рациональным является сечение двутавра с наибольшим коэффициентом металлоемкости .

4.8 Вопросы и ответы для самоконтроля

1. Какое состояние стержня называется чистым изгибом?

Состояние стержня, при котором в его сечениях действует только изгибающий момент или , называется чистым изгибом.

2. Какое состояние стержня называется поперечным изгибом?

Состояние стержня, при котором в его сечениях действуют поперечная сила и изгибающий момент , называется поперечным изгибом.

3. Какая линия называется упругой линией балки ?

Изогнутая ось балки называется упругой линией балки.

4. Какой слой сечения называется нейтральным ?

Слой поперечного сечения балки, в котором нормальные напряжения и деформации растяжения-сжатия равны нулю, называется нейтральным.

5. Формула для определения нормальных напряжений в любой точке сечения. . Нормальное напряжение в любой точке сечения прямо пропорционально изгибающему моменту и ее расстоянию до нейтрального слоя и обратно пропорционально осевому моменту инерции сечения относительно оси х.

6. Формула для определения максимального нормального напряжения.

. Максимальное нормальное напряжение прямо пропорционально изгибающему моменту и обратно пропорционально осевому моменту сопротивления сечения относительно оси .

7. Закон распределения нормальных напряжений при изгибе.

Нормальные напряжения при изгибе распределяются по высоте сечения по закону прямой от нуля в нейтральном слое до максимальной величины в наиболее удельных точках поверхностных слоев сечения.

8. Формула для определения кривизны изогнутой оси балки.

. Кривизна изогнутой оси балки прямо пропорциональна уравнению изгибающего момента в сечениях балки.

9. Условие прочности по нормальным напряжениям при изгибе.

. Максимальное нормальное напряжение, прямо пропорционально изгибающему моменту и обратно пропорционально осевому моменту сопротивления, не должно превышать величины допускаемого нормального напряжения.

10. Решение задач на основе условия прочности

Проектировочная задача определения размеров сечения

Проверочная задача определения допускаемого изгибающего момента .

Проверочная задача проверки прочности и определения действительного коэффициента запаса прочности , .

11.Формула для определения касательных напряжений при поперечном изгибе.

. Касательные напряжения прямо пропорциональны

поперечной силе и статическому моменту отсеченной части сечения относительно центральной оси , и обратно пропорциональны ширине исследуемого слоя и осевому моменту инерции сечения относительно центральной оси .

12. Закон распределения касательных напряжений.

Касательные напряжения по высоте прямоугольного, круглого сечений и сечений типа двутавр, швеллер распределяются по закону квадратной параболы от нуля в точках поверхностных слоев до максимального значения в точках нейтрального слоя.

13. Где в сечении касательные напряжения изменяются скачкообразно?

Касательные напряжения изменяются скачкообразно при уменьшении или увеличении ширины сечения.

14. Условие прочности по касательным напряжениям

. Максимальное касательное напряжение, прямо пропорционально поперечной силе и статическому моменту полусечения относительно центральной оси , и обратно пропорционально ширине нейтрального слоя и осевому моменту инерции сечения относительно оси и не должно превышать допускаемого касательного напряжения.

15. Что показывает осевой момент сопротивления ?

Осевой момент сопротивления сечения показывает способность поверхностных точек сечения сопротивляться деформациям растяжения- сжатия при изгибе.

16. Что показывает жесткость балки при изгибе ?

Жесткость балки при изгибе показывает способность сечения сопротивляться деформациям растяжения-сжатия при изгибе.

17.Какое напряженное состояние испытывает материал в сечениях балок при чистом изгибе ?

Материал во всех точках поперечных сечений балок, испытывает линейное напряженное состояние.

18. Какое напряженное состояние испытывает материал в сечениях балок при поперечном изгибе ?

Материал во всех точках поперечных сечений балок кроме точек наиболее удаленных поверхностных и нейтральных слоев, испытывает плоское напряженное состояние.

19. Как записываются условия прочности по эквивалентным напряжениям.

,

Таблица основных формул для простых состояний стержней

Состояние стержня	Отно ситель-ная деформация	Закон Гука и распределение напряжений	Условие прочности	Условие жесткости
Растяжение-сжатие
Сдвиг
Кручение
Чтстый поперечный изгиб