7. Определение геометрических параметров передачи

Расчёт геометрических параметров рассматриваемой зубчатой передачи проводят согласно ГОСТ 16532 – 70. Формулы для определения основных геометрических параметров цилиндрических зубчатых зацеплений представлены в табл. П6 приложения. Исходными данными при расчёте являются:

- межосевое расстояние a_ω(Н,F), определённое по контактным или изгибным напряжениям;

- нормальный модуль зацепления m_n, определённый по изгибным напряжениям.

Алгоритм расчёта параметров передачи представлен на рис. 11.

aω(Н,F) = … , мм; mn = … , мм

β1 = … , град

z∑ = … , z1 = … , z2 = … , ui = … , β = … , град

aω или aω(Н,F)

Уточнение β = … , град

х∑ = … , х1 = … , х2 = … , у = … , ∆у = …

d1 = … , мм; dω1 = … , мм; d2 = … , мм; dω2 = … , мм;

Рис. 11. Алгоритм расчёта параметров зацепления

7.1. Расчёт параметров зацепления

Для достаточно узких зубчатых колёс коробок передач достаточным является условие, при котором коэффициент осевого перекрытия ε_β = 1. Угол наклона β¹, удовлетворяющий условию ε_β = 1, будет равен:

β¹ = arcsin . (7.1)

Суммарное приведённое число зубьев z_{∑ пр} определяют по формуле:

z_{∑ пр} = z₁ + z₂ = . (7.2)

Величину z_{∑ пр} округляют до целого меньшего числа z_∑ и находят уточнённое значение угла наклона линии зуба:

β = arccos . (7.3)

Для определения чисел зубьев шестерни z₁ и колеса z₂ используют значение передаточного числа u_i:

z₁ = . (7.4)

Для шестерни первой передачи двухвальной коробки передач количество зубьев z_{ш min} ≥ 12. Как правило, для трёхвальных КП легковых автомобилей количество зубьев шестерни постоянного зацепления z_ш = 15…19; грузовых – z_ш = 17…28.

Численное значение z₁округляют до целого меньшего числа, после чего определяют число z₂ (z₂ = z_∑ – z₁). По найденным значениям чисел зубьев шестерни и колеса уточняют передаточное число зацепления u_i. По полученным значениям уточняют межосевое расстояние а_ω, значение которого должно быть не менее a_ω(Н,F):

а_ω = 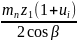≥ a_ω(Н,F). (7.5)

Если неравенство (7.5) не выполняется, (то есть а_ω < a_ω(Н,F)), то окончательно выбирают межосевое расстояние a_ω(Н,F), определённое по контактным или изгибным напряжениям. После этого корректируют угол наклона зуба β (7.6), количество зубьев колёса z₂ и передаточное число u_i (7.2) … (7.4):

β = arccos , (7.6)

Выбранное наибóльшее значение межосевого расстояния а_ω определяют с учётом изменения угла зацепления (из – за смещения исходного контура) по формуле:

а_ω = 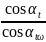, (7.7)

где z₁ и z₂ – числа зубьев шестерни и колеса соответственно;

α_t – делительный угол зацепления в торцовом сечении, град;

α_tω – угол зацепления в торцовом сечении зубчатого зацепления, выполненного со смещением исходного контура, град.

Определим угол зацепления α_tω , выразив его из формулы (7.7):

α_tω = arccos . (7.8)

В общем случае угол α_tω определяют по инвалюте (таблица П7 приложения):

inv α_tω = inv α_t + , (7.9)

где х₁ и х₂ – коэффициенты смещения исходного контура шестерни и колеса соответственно.

Согласно (7.9), суммарный коэффициент смещения х_∑ будет равен:

х_∑ = х₁ + х₂ = 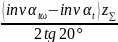≤ 1. (7.10)

Значение х_∑ округляют до тысячных. Для увеличения х_∑ с целью повышения прочности зубьев можно уменьшить z_∑ на один – два зуба. Таблица инвалют приведена в таблице П8 приложения.

Для коробок передач автомобилей зубчатая передача, в которой число зубьев шестерни z_ш ≥ 23 и передаточное число u_i ≥ 1,5, может выполняться без смещения (коэффициенты смещения шестерни и колеса х_ш = х_к = 0). При z_ш < 23 и u_i ≥ 2 передачу обычно выполняют равносмещённой (х_ш = – х_к, х_ш > 0) или смещённой (х_ш = х_к, х_∑ > 0). При z_ш < 23 и u_i < 2 передачу выполняют смещённой. Примерное значение коэффициентов смещения х₁ и х₂ для смещённой передачи можно определить в соответствии с передаточным числом, учитывая при этом, что бóльшее смещение берут в сторону шестерни:

х_ш = х₁ = , х_к = х₂ = х_∑ – х₁. (7.11)

Для равносмещённой передачи х₁ = х₂. На выбор смещений могут влиять геометрические параметры. Например, если при определённом модуле и одинаковых углах наклона β требуется выполнить соседние пары зубчатых колёс с различным суммарным числом зубьев z_∑, то это достигается введением смещений.

Делительный d и начальный d_ω диаметры шестерни и колеса определяют по формулам, представленным в табл. П6 приложения.