Геоцентрическая система координат
Заметим, что геодезическая и геоцентрическая долготы совпадают. Обе они определены как двугранный угол между плоскостью нулевого меридиана и плоскостью, содержащей ось вращения и заданную точку. Геоцентрическая же широта отличается от геодезической.
Рассмотрим точку P, лежащую вне ОЗЭ. Опустим из этой точки перпендикуляр на поверхность эллипсоида и продолжим его до пересечения с экваториальной плоскостью (рис2) Проекцию точки P на поверхность эллипсоида обозначим через Q. Тогда отрезок PQ есть геодезическая высота точки Р. Угол, под которым упомянутый перпендикуляр пересекает плоскость экватора, есть геодезическая широта B. Она относится как к точке Q, так и к точке Р. Геоцентрические широты этих двух точек, как видно из рисунка, различаются. Геоцентрическая широта точки Q угол Ф между радиус-вектором этой точки и плоскостью экватора.
Установим связь
между координатами точки Q, сжатием
эллипсоида
и
широтами В и Ф. Поскольку точка
Q лежит на поверхности эллипсоида,
то её прямоугольные координаты
подчиняются
уравнению эллипсоида вращения:
.
Рассмотрим сечение y=0. Тогда, как
легко видеть,
.
Чтобы определить tgВ, нужно найти
угловой коэффициент нормали в точке Q.
Уравнение нормали к кривой F(x ,z) =0
в точке
имеет
вид
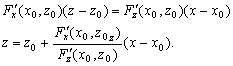(3)
У нас
поэтому
Следовательно,
Определим отличие геоцентрической широты Ф от геодезической В. Имеем очевидные равенства
.
(4)
Второй эксцентриситет
эллипса, как мы знаем, определяется
следующим образом
,
поэтому
.
Для Земли второй
эксцентриситет мал, поэтому, пренебрегая
малыми второго порядка относительно
сжатия, получим
.
Можно также считать, что
Учитывая
сказанное, получим
Наибольшее отличие
геодезической широты от геоцентрической
достигается на широте 45
и составляет
.
Связь глобальных декартовых координат с геоцентрическими определяется формулами (1). Определим теперь формулы, связывающие декартовы координаты с геодезическими. Это означает, что бы должны определить координаты точки Р через параметры эллипсоида и геодезические широту и долготу.
Поскольку
,
для определения координат x, y ,z точки
Р достаточно, для начала, определить
только координаты x и z . то есть
все рассуждения проводить только для
сечения у =0. Обратимся к рис. 3.
Определим прямоугольные координаты точки Р, расположенной на высоте Н над поверхностью эллипсоида. Сначала определим координаты проекции точки Р на поверхность эллипсоида ( точка Q). Её координаты в сечении Охz равны
Индексом “0” мы отметили принадлежность координат к точке, лежащей на поверхности эллипсоида. Как мы видели
поэтому
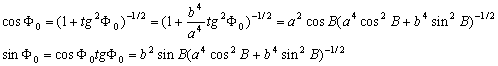
Остаётся определить радиус-вектор точки Q. Воспользуемся уравнением эллипса и выполним необходимые преобразования.
(5)
Выразим
и
через
cosB и sinB, для чего воспользуемся
приведёнными выше формулами. Определим
радиус-вектор точки Q
следовательно,
(6)
Обозначим
.
(7)
Теперь
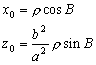(8)
Для произвольного
сечения, проходящего через ось вращения
,будем
иметь
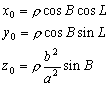(9)
Теперь поднимем точку Q на высоту Н и совместим её с точкой Р. Прямоугольные координаты изменятся на
(10)
Окончательно, теперь формулы для пересчёта геодезических координат B, L и Н в прямоугольные x,y,z примут вид
(11)
Здесь
,
определённый формулой (7) имеет простой
геометрический смысл: он равен отрезку
нормали, проходящей через точку Q,
от этой точки до точки пересечения её
с осью вращения эллипсоида. Справедливость
этого утверждения предлагается доказать
самостоятельно.