Поликонические проекции (policonic projection)

При получении поликонической проекции проецирование осуществляется для каждой параллели на свой конус. Все точки лежащие на параллели, по которой происходит касание, переносят на конус. Для следующей параллели берется другой конус и на него также отображаются соответствующеие точки. Все конусы будут разные. Чем южнее параллели, тем конусы будут более острые.

При проецировании выберается один меридиан, который называют осевым. Место пересечения меридиана с параллелями фиксируется особыми точками.

После этого конусы разрезаются вдоль мериана противоположного осевому. При наложении конусов, зафиксированных по осевому меридиану, получают дуги, соответствующеие параллелям и симметричные относительно осевого меридиана.

Разрывы между вырезанными дугами заполняют соответствующими изображениями земной поверхности.

Осевой меридиан на полученной проекции будет представлен прямой линией, проходящей через середину карты, а параллели - дугами окружностей, центры которых не будут совпадать, но будут лежать на осевом меридиане. Расстояние между параллелями будет увеличиваться по мере удаления от осевого меридиана.

Осевой меридиан является одним из параметров проецирования.

К поликоническим проекциям в широком понимании относятся проекция Таича (определялась аналитически) и проекции Гинзбурга (получены численными методами).

Рис. 5.4. Поликоническая проекция

Видоизмененная простая поликоническая проекция (продолжение надо)

Она применяется как многогранная Земная поверхность, принимаемая за поверхность эллипсоида вращения, делится линиями меридианов и параллелей на трапеции.

При рассмотрении данной проекции учтем особенности ее применения при создании карты масштаба 1:1 000 000.

Трапеции изображаются на отдельных листах в одной и той же проекции (для карты масштаба 1:1 000 000 -в видоизмененной простой поликонической).

Листы международной карты мира масштаба 1:1 000 000 имеют определенные размеры сторон трапеций: по меридианам - 4°, по параллелям - 6°; на широте от 60 до 76° листы сдваивают, они имеют размеры по параллелям 12°; выше 76° листы счетверяют, их протяжение по параллелям - 24°.

Применение проекции как многогранной определяет необходимость введения номенклатуры - системы обозначения отдельных листов.

Цилиндрические проекции (cylindrical projection)

По свойствам изображения проекции могут быть равноугольными, равновеликими и произвольными. Применяются прямые, косые и поперечные цилиндрические проекции в зависимости от расположения изображаемой области.

В прямых цилиндрических проекциях параллели и меридианы изображаются двумя семействами параллельных прямых линий, перпендикулярных друг другу. Таким образом задается прямоугольная сетка цилиндрических проекций.

Промежутки между параллелями пропорциональны разностям долгот. Промежутки между меридианами определяются принятым характером изображения или способом проектирования точек земной поверхности на боковую поверхность цилиндра. Из определения проекций следует, что их сетка меридианов и параллелей ортогональна.

Масштаб, определенный вдоль параллелей, будет, очевидно, разный, но в то же время одинаковый по  меридианам. Эта проекция по характеру искажений будет произвольной, потому что и углы и площади объектов карты будут искажены.

Если при проецировании трапеции, образованные параллелями и меридианами, преобразовались в квадраты, то такую проекцию иногда называют квадратной.

Чтобы получить равновеликую проекцию, необходимо сжать расстояние между параллелями, тем больше, чем дальше они от экватора, а чтобы получить равноугольную проекцию - очень сильно растянуть.

Прямая цилиндрическая равноугольная проекция носит имя Меркатора, она разработана в 1569 году. Именно эта проекция используется в ГИС для построения топографических карт, но только не в виде прямой проекции, а в виде поперечной.

При получении цилиндрических проекций можно использовать цилиндры, которые будут касаться эллипсоида, по эватору, или пересекать его по двум параллелям, симметричным относительно экватора. Если цилиндр касается экватора, то получится цилиндрическая проекция с одной стандартной параллелью, если цилиндр пересекает эллипсоид, то стандартных параллелей две.

В прямых цилиндрических проекциях одинаково изображаются одни и теже участки земной поверхности вдоль линии разреза - по восточной и западной рамкам карты (дублируемые участки карты) и обеспечивает удобство чтения по широтным поясам (например, на картах растительности, осадков) или по меридианальным зонам (например, на картах часовых поясов).

В прямых проекциях полюс показывается прямой линией, по длине равной экватору, но в некоторых из них (проекции Меркатора) отобразить невозможно.

В косых и поперечных цилиндрических проекциях меридианы и параллели изображаются различными кривыми, но средний меридиан проекции, на котором располагается полюс косой системы, всегда прямой.

Косые цилиндрические проекции при широте полюса косой системы близкой к полярным широтам, имеют географическую сетку, дающую представление о сферичности земного шара. С уменьшением долготы полюса кривизна параллелей увеличивается, а их протяженность уменьшается, поэтому уменьшаются и искажения (эффект сферичности).

Полюс представляется точкой в косык и поперечных проекциях. При ширине полосы до 4,5° можно использовать касательный цилиндр, при увеличении ширины полосы следует применять секущий цилиндр, т е. вводить редукционный коэффициент.

В ГИС, при определении собственной цилиндрической проекции, требуется задать точку, где будет проходить ось цилиндра и одну или две параллели (или их аналоги в случае косой и поперечной проекций), где цилиндр будет касаться или пересекать эллипсоид. Также требуется определить способ проецирования на основе имеющегося в ГИС алгоритма, выбрав название проекции, на основе которой Вы хотите создать свою собственную.

Цилиндрические проекции можно рассматривать как частный случай конических при а=0 (вершина конуса в бесконечности). Они применяются при составлении карт мелких и крупных масштабов – от общегеографических до специальных (аэронавигационные маршрутные полетные карты).

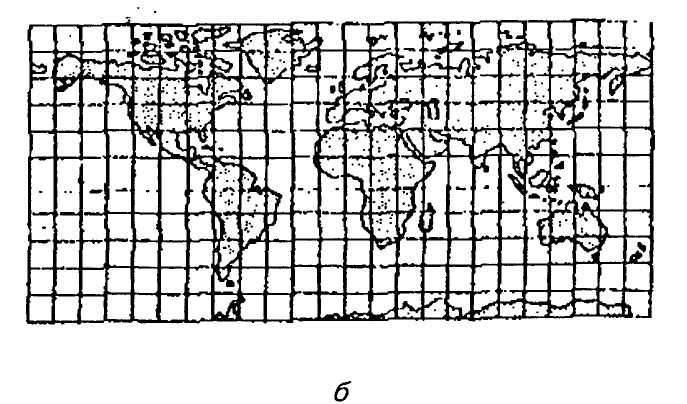
Рис. 5.3. Цилиндрическая проекция:

а - принцип построения проекции;

б - вид проекции