Классификация проекций по характеру и размеру искажений
равноугольные проекции (conformal projection), которые сохраняют без искажений углы и формы малых объектов, но в них резко деформируются длины и площади объектов. В математике такие преобразования называют конформными. Этот вид проекций приемлем для прокладки маршрутов транспортных средств.
равновеликие проекции (equivalente projection) не искажают площадей (с учетом масштаба), но в них искажены углы и формы объектов. Применяется для определения площадей и землепользования
произвольные проекции (arbitrary projection) имеют искажения углов, площадей и длин, но эти искажения распределены по карте, например, так, что минимальные искажения имеются в центральной части и возрастают к краям. Среди произвольных проекций выделяют равнопромежуточные (equidistant projection), в которых искажения длин отсутствуют по одному из направлений: вдоль меридиана или вдоль параллели. Масштаб при такой проекции в разных местах карты разный.
Классификация проекций по способу проецирования
Бывают проекции на плоскость, конус и цилиндр. Плоские карты из конуса и цилиндра получаются разворачиванием их на плоском столе.
Конические проекции (konical projection).
Образование конических проекций можно представить как проектирование земной поверхности на боковую поверхность конуса, определенным образом ориентированного относительно земного шара (эллипсоида). После проектирования боковая поверхность конуса разрезается по одной из образующих и развертывается в плоскость.
Способ ориентировки конуса относительно эллипсоида определяет три вида проекций:
прямые, в которых ось конуса совпадает с малой осью эллипсоида. При этом конус берется или касательный, или секущий. Касание осуществляется по одной параллели, сечение - по двум параллелям. Параллели, в которых конус пересекает или касается эллипсоида, называются стандартными. По стандартным параллелям искажения минимальны.
поперечные, в которых ось конуса совпадает с большой осью эллипсоида;
косые, в которых ось конуса не совпадает ни с большой, ни с малой осями, но по-прежнему проходит через центр эллипсоида.
Если проекция не прямая, то касание или сечение эллипсоида производится не по параллелям.
В прямых конических проекциях меридианы изображаются прямыми линиями, сходящимися в одной точке. Углы между меридианами пропорциональны разностям долгот между ними. Параллели изображены дугами окружностей, имеющими один общий центр. Параллели и меридианы пересекаются под углом 90 градусов.
По характеру искажений конические проекции могут быть равноугольные, равновеликие и произвольные. Наибольшее распространение получили равноугольные и равнопромежуточные проекции.
В равнопромежуточных конических проекциях расстояния между параллелями одинаковые, а по меридианам одинаковый масштаб. По характеру искажения равнопромежуточные проекции относятся к произвольным.
При проектировании по методу линейной перспективы получаются перспективные конические проекции, обладающие только промежуточными свойствами по характеру искажений.
В аналитическом представлении конических проекций имеются две константы а и с. Постоянная а равняется синусу широты стандартной параллели или, что то же самое, синусу угла при вершине конуса. Коническая проекция данной группы вполне определяется, если заданы постоянные проекции или любые величины, с ними связанные. Это могут быть широты стандартных или крайних параллелей. В последнем случае, например, может быть дополнено условие, чтобы масштабы на крайних параллелях и на параллели с наименьшим масштабом были равны по абсолютной величине.
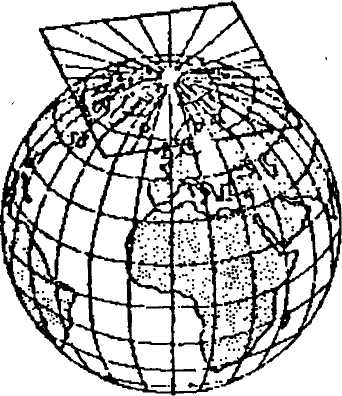
Рис. 5.1. Коническая проекция:
а - принцип построения проекции;
б - вид проекции