
- •Раздел 1. Линейные электрические цепи переменного тока
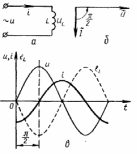
- •Основные параметры переменного тока.
- •2. Метод векторных диаграмм.
- •3 . Правила Кирхгофа.
- •4. Активное сопротивление в цепи переменного тока
- •5. Емкость в цепи переменного тока
- •6. Индуктивность в цепи переменного тока
- •7 .Неразветвленная цепь переменного тока
- •8. Активная, реактивная и полная мощность
- •9.Резонанс напряжений
- •10. Разветвленная цепь переменного тока
- •11.Резонанс токов
6. Индуктивность в цепи переменного тока
Приложено u = Umsinωt (1), известно L.
Найдем ток i = Imsin(ωt + α0); т.е. Im и α0
По второму правилу Кирхгофа: u + eL = 0 (5)
( 6)
eL
=
-dФ/dt
= - L
di/dt
– закон электромагнитной индукции.
6)
eL
=
-dФ/dt
= - L
di/dt
– закон электромагнитной индукции.
(6)(5) u - L di/dt = 0 di/dt = u/L = Um/L sinωt
после интегрирования:
i = (Um/ωL) cosωt = Im sin(ωt – π /2) (7)
α0 = - π/2 Ток отстает по фазе от напряжения на π /2. Построим ВД.
Im = Um/(ωL)
Im/(2)1/2 = Um/(ωL(2)1/2) I = U/ωL
ωL = XL – индуктивное сопротивление
I = U/XL - закон Ома для цепи переменного тока с индуктивностью. Мгновенная мощность:
p = iu = ImUmsinωt sin (ωt - π /2) = - IU sin 2ωt
Средняя мощность за период: p = 0
Синусоида тока сдвинута на π /2 или на T/4 к концу оси.
В нечетных четвертях p < 0, энергия возвращается из катушки в источник.
В четных четвертях p > 0, энергия передается в катушку.
Средняя мощность за период Pср = 0
7 .Неразветвленная цепь переменного тока
(Последовательное соединение R,L,C)
П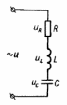 режняя
формулировка задачи:
режняя
формулировка задачи:
приложено синусоидальное напряжение и найти ток.
Изменим формулировку задачи:
Синусоидальное напряжение вызывает в линейной цепи синусоидальный ток и наоборот.
Дано: i = Imsin(ωt); известны R, L, C.
Необходимо найти u = Umsin(ωt+ φ ) (1); т.е. Um и φ
u = uR + uc + uL (2) второе правило Кирхгофа
uR = iR = Umr sinωt, UmR = ImR;
uc = iXc= Umcsin(ωt - π/2), Umc = Im 1/ωC;
uL= iXL = UmL sin(ωt + π /2), UmL = Im ωL;
Н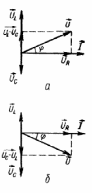 айти
U
по (2) трудно и не точно, поэтому используем
МВД, т.е. запишем (2) в векторном форме:
айти
U
по (2) трудно и не точно, поэтому используем
МВД, т.е. запишем (2) в векторном форме:
Ū = ŪR + Ūc + ŪL (2’)
Для определения Ū построим векторную диаграмму напряжений
В качестве основного вектора выберем Ī.
Векторы ŪR ,Ū и (Ūc + ŪL) образуют треугольник напряжений.
Из треугольника напряжений Um = (U2mR + (UmL - Umc)2) 1/2 (3)
Для определения начальной фазы φ и полного сопротивления цепи Z разделим векторы треугольника напряжений на ток I, получим треугольник сопротивлений.
UR/I = R, (UL – Uc )/I = UL/I – Uc/I = XL – Xc = X - реактивное сопротивление.
U/I = Z - полное сопротивление.
И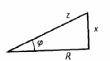 з
треугольника сопротивлений:
з
треугольника сопротивлений:
Z = (R2 + x2)1/2 = (R2+ (XL-Xc)2)1/2= (R2 + (ωL–1/ ωC)2)1/2 (4)
Закон Ома для последовательной цепи:
I= U/Z = U/ (R2 + (ωL – 1/ ωc)2)1/2
tgφ = X/R = (ωL – 1/ ωC)/R; φ = arctg (ωL – 1/ ωc)/R (5)
В формуле u = Um sin (ωt + φ) все известно.
8. Активная, реактивная и полная мощность
У множим
вектора треугольника напряжений на ток
I.
множим
вектора треугольника напряжений на ток
I.
UR*I = P – активная мощность S Q
(UL – UC) *I = Q – реактивная
U *I
= S – полная
*I
= S – полная
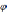
Получили треугольник мощностей
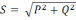 ;
;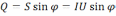
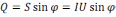 Р
Р

Рассчитаем активную мощность как среднюю за период:
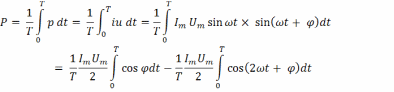
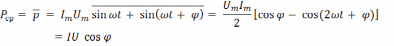
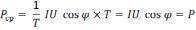
P – измеряется в ваттах. Её значения показывают ваттметры. Соответствует той части электрической энергии, которая превращается в другие виды энергии в потребителя и не возвращается в источник.
Q – измеряется в ВАр и кВАр, соответствует электрической энергии, которая возвращается в источник.
S– измеряется в ВА и кВА. Указывается в паспорте двигателей.
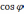 – коэффициент мощности.
– коэффициент мощности.
Интересно,
что 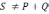 (но
(но 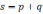 –мгн.
знач. мощности).
–мгн.
знач. мощности).
