3 . Правила Кирхгофа.

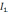
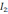
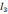
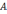
Первое правило: алгебраическая сумма токов в узле электрической цепи равна нулю

∑ⁿ_k=1 I_k = 0, если I₁, I₃ > 0 тогда I₂, I₄ < 0, можно наоборот.

Первое правило является следствием закона сохранения заряда, поэтому правило Кирхгофа, а не закон.

Второе правило: в замкнутом контуре электрической цепи алгебраическая сумма падений напряжений на участках контура равна алгебраической сумме ЭДС, действующих в этом же контуре.

∑ⁿ_k=1 U_k = ∑^m_n=1E_n

Е и U могут иметь различные знаки при обходе контура.

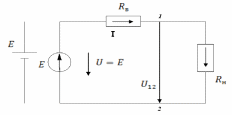
Положительные направления Е и U показываются стрелками.

За положительное направление тока принято направление движения положительных зарядов.

За положительное направление U принято направление убывания потенциала.

U₁₂ = φ₁ – φ₂, U₁₂ > 0, если φ₁ > φ₂

В пассивных элементах, т.е. R, L, C положительное направление U совпадает с положительным направлением тока.

За положительное направление Е принято направление действия сторонних сил в источнике (от «-» к «+» внутри источника).

При обходе контура значения Е и U берутся положительными, если их положительное направление совпадает с направлением обхода.

Второе правилo Кирхгофа есть следствие закона сохранения энергии

Σ U_к ·q = Σ Е_n ·q Работа сторонних сил (правая сумма) равна работе электрических сил по перемещению зарядов (левая сумма)

4. Активное сопротивление в цепи переменного тока

Дано: приложенное: u = U_m sinωt (1), известно R.

Найти ток i = I_msin(ωt + α₀); т.е. найти: I_m и α₀

Т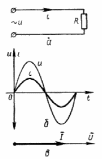 ок i = u /R = (U_m/R) sinωt = I_msinωt (2);

1) I_m = U_m /R, I_m/(2)^1/2 = U _m/R(2)^1/2; I = U/R - закон Ома для цепи ПэТ, содержащей активное сопротивление.

2) Фазы совпадают ( α₀ = 0) и частоты тоже. Построим ВД.

3) Мгновенная мощность:

p = iu = I_mU_msin²ωt = (I_mU_m / 2) (1 – cos 2ωt) =

= IU(1 – cos 2ωt) (3)

1. p ≥ 0 всегда

2. изменяется с частотой 2ω

Графики тока, напряжения и мощности на рисунке.

Найдем среднее за период значение мощности:

P_ср = 1/T ∫^T₀ pdt = IU/T ∫^T₀ dt – IU/T ∫^T₀ cos(2ωt) dt = (IU/T)T = IU. Для ФТС: P_ср = ¯р = IU(1 – ¯cos 2ωt) (3)

P_ср= IU= I²R (удобство использования действующих величин)

Средняя за период мощность называется активной, а соответствующее ей сопротивление активным сопротивлением R = Р/ I²

Активное сопротивление не обязательно омическое. Оно может быть обусловлено любым преобразованием электрической энергии в другие виды.

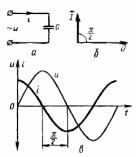
5. Емкость в цепи переменного тока

Дано: приложенное u = U_msinωt, известно С.

Найти ток i = I_msin(ωt + α₀); т.е. I_m и α₀

i = dq/dt; q-заряд на обкладках конд-ра.

С = q/u_c – емкость конденсатора по определению.

u_c = u  q = Cu  i = Cdu/dt = CωU_m cosωt;

i = I_m sin(ωt + π/2); (4)

ток опережает напряжение на π/2  α₀ = π /2

1)Построим ВД.

2)I_m = ωCU_m  I_m/(2)^1/2 = ωCU_m/(2)^1/2 

I = U/(1/ωC)  1/ ωC = X_c емкостное сопротивление

I = U/X_c – закон Oма для цепи ПеТ, содержащей емкость.

3) Мгновенная мощность:

р = iu = I_mU_msinωt sin(ωt + π/2) = (I_mU_m/2)sin2ωt = IUsin2ωt;

Sinα sinβ = ½ [cos(α - β) - cos(α + β)], (cos(2ωt + π/2) = sin2ωt);

Средняя за период мощность

p_ср = 1/T ∫^T₀ pdt = IU/T ∫^T₀ sin (2ωt) dt = 0.

(ОТД P_ср = IU¯sin2ωt = 0) – нет превращения электрической энергии в другие виды энергии.

Рассмотрим графики.

Синусоида тока сдвинута на π/2 к началу оси или T/4

t = T  α = (2π/T)t = 2 π ; α = π /2  t = T/4

в нечетных четвертях p > 0, энергия передается в потребитель – конденсатор заряжается W = CU²/2

в четных четвертях p < 0, энергия возвращается в источник, конденсатор разряжается. Среднее значение P_ср = 0!