Расчет номиналов емкостей и сопротивлений для arc-фильтра нижних частот

2-го порядка

Передаточная функция любого фильтра нижних частот может быть представлена в следующей форме:

(1.30)

Порядок фильтра n определяется максимальной степенью s в выражении (1.30) после того, как выполнено перемножение блоков второго порядка в знаменателе. Он задает асимптотический наклон амплитудно-частотной характеристики коэффициента передачи, равный —n∙20 дБ на декаду. Вид частотной характеристики определяется как порядком, так и типом фильтра. В качестве ARC-фильтров наибольшее применение находят фильтры Баттерворта, Чебышева и Бесселя, которые отличаются лишь значениями коэффициентов a_i и b_i передаточной функции (1.30).

На основании выражения (1.30) запишем в общем виде передаточную функцию фильтра нижних частот второго порядка:

(1.31)

Фильтр со сложной отрицательной обратной связью

Передаточная функция инвертирующего активного фильтра нижних частот 2-ого порядка, изображенного на рис. 9, описывается выражениями (1.29). Приравняв коэффициенты этой передаточной функции коэффициентам выражения (1.31), получим:

(1.32)

(1.33)

(1.34)

Для расчета фильтра можно, например, задать значения сопротивлений R₁ и R₃ и по приведенным формулам вычислить значения R₂, C₁ и C₂. Как видно, расчетные формулы справедливы для произвольных положительных значений a₁ и b₁. Коэффициент передачи постоянного сигнала фильтра оказывается отрицательным, поэтому прошедший через фильтр низкочастотный сигнал будет инвертирован.

Чтобы реальная схема фильтра имела желаемую амплитудно-частотную характеристику, некоторые входящие в нее элементы могут быть подобраны НЕ с очень высокой точностью. Даже для НЕинтегральной реализации фильтра (на дискретных компонентах) не возникнет проблем при подборе резисторов, поскольку для прецизионных резисторов номиналы задаются с однопроцентным допуском. Однако, несколько хуже обстоит дело с конденсаторами, так как реальный допуск их номинальных значений, как правило, составляет 10 % и более.

При производстве ИМС необходимо учитывать размеры и взаимное расположение резисторов, поскольку от этого зависит как точность их изготовления, так и стабильность характеристик при различных температурах окружающей среды. При разумном проектировании относительная погрешность интегральных резисторов может быть менее 1%. Относительная погрешность номиналов интегральных конденсаторов площадью более (мкм)² составляет менее %.

При расчете, как правило, задаются (фиксируются) номиналы тех элементов, которые имеют наименьшую согласованность, а рассчитываются элементы, номиналы которых могут иметь меньшую абсолютную или относительную погрешность. В качестве иллюстрации приведем расчет с заданными равными значениями емкостей и вычисляемыми значениями резисторов. При выполнении расчетов к лабораторной работе, необходимо для фильтров задавать значения сопротивлений и вычислять значения емкостей. Решим уравнения относительно сопротивлений:

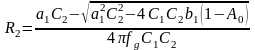, (1.35)

, (1.36)

. (1.37)

Для того чтобы значение сопротивления R₂ было действительным, должно выполняться условие:

. (1.38)

Характеристики фильтра мало зависят от точности подбора номиналов его элементов, поэтому рассмотренная схема может быть рекомендована для реализации фильтров с высокой добротностью.