
- •//////////////// Лабораторная работа №1 по курсу «Основы схемотехники» «Изучение простейших линейных схем аналоговой обработки сигналов»
- •Теоретическая часть
- •Примеры расчета передаточных функций некоторых пассивных линейных схем
- •Пассивный rc фильтр низких частот первого порядка
- •Простейшие активные линейные схемы аналоговой обработки сигналов. Начальные сведения об операционном усилителе
- •Полностью дифференциальный операционный усилитель
- •Паразитные эффекты в оу
- •Аналоговой обработки сигналов.
- •Инвертирующий усилитель
- •Повторитель, неинвертирующий усилитель и неинвертирующий сумматор
- •Сумматор-вычитатель
- •Активный инвертирующий интегратор
- •Активный инвертирующий rc-фильтр нижних частот 2-го порядка (со сложной отрицательной обратной связью)
- •Неинвертирующий активный фильтр нижних частот второго порядка (со сложной положительной обратной связью)
- •Расчет номиналов емкостей и сопротивлений для arc-фильтра нижних частот
- •Фильтр со сложной отрицательной обратной связью
- •Фильтр с положительной обратной связью
- •Способы задания оптимальных характеристик фильтров нч
- •Фильтр Баттерворта
- •Фильтр Чебышева
- •Фильтр Бесселя
- •Неинвертирующий активный базовый элемент на базе оу
- •Инвертирующий arc интегратор
- •Список рекомендуемой литературы:
//////////////// Лабораторная работа №1 по курсу «Основы схемотехники» «Изучение простейших линейных схем аналоговой обработки сигналов»
Цель работы: Освоение процесса моделирования с использованием Cadence Virtuoso Schematic Editor & Virtuoso Symbol Editor, Analog Artist Simulation. Изучение простейших линейных схем аналоговой обработки сигнала.
Задание:
Провести частотный (AC Analysis) анализ схемы пассивного RC-фильтра НЧ первого порядка.
Провести временнόй (Transient) анализ схем инвертирующего или неинвертирующего усилителя (согласно варианту)
Провести анализ схемы активного инвертирующего интегратора.
Провести частотный и временнόй анализ схемы активного фильтра НЧ второго порядка (согласно варианту).
Теоретическая часть
В аналоговой схемотехнике рассматриваются схемы аналоговой обработки сигнала. По умолчанию предполагается, что сигнал представляет собой переменное и непредсказуемое значение либо тока, либо напряжения. Если бы его значение всегда можно было бы предсказать, этот сигнал потерял бы для нас интерес, и для его обнаружения и измерения не требуется создавать аналоговые схемы.
Осциллограмма типового сигнала (например, человеческая речь) выглядит шумоподобно (Рис. 1), то есть ее значения, как превышающие некоторую постоянную составляющую (отсутствие сигнала), так и меньшие ее, являются равновероятными.

Рис. 1 – Осциллограмма типового сигнала
По этой причине практически в любом аналоговом узле в качестве постоянной составляющей напряжения (напряжение на сигнальном проводе при отсутствии сигнала) принято напряжение, равноудаленное от потенциалов источника (источников) питания. В случае одного источника питания потенциал постоянной составляющей равен половине напряжения питания, т.е. Vdda/2. Ввиду особого его расположения и значения, этот потен циал называют потенциалом «аналоговой земли» Vgnda.
Примеры расчета передаточных функций некоторых пассивных линейных схем
Для характеризации
линейных
схем используется передаточная
функция,
которая представляет собой дифференциальный
оператор, выражающий связь между входом
и выходом системы. Зная входной сигнал
и передаточную функцию системы можно
восстановить выходной сигнал. Почему
передаточная
функция является атрибутом только
линейных схем? Ответ
заключается в следующем: линейная
функция
 по определению
является линейной для любой
величины входного сигнала
по определению
является линейной для любой
величины входного сигнала
 ,
поэтому, рассчитывая или измеряя
передаточную функцию линейной или
«почти» линейной (линейной с приемлемо
малой погрешностью) системы для некоторого
диапазона уровней входного сигнала, мы
должны быть уверенными в её линейности
и для расширенного диапазона уровней
входного сигнала.
,
поэтому, рассчитывая или измеряя
передаточную функцию линейной или
«почти» линейной (линейной с приемлемо
малой погрешностью) системы для некоторого
диапазона уровней входного сигнала, мы
должны быть уверенными в её линейности
и для расширенного диапазона уровней
входного сигнала.
Пусть x(t)
– входной сигнал линейной стационарной
системы, а y(t)
– её выходной сигнал. Тогда передаточная
функция H(s)
такой системы будет описываться
выражением
 ,
где Y(s)
и X(s)
соответственно преобразования Лапласа
для сигналов y(t)
на выходе и x(t)
на входе линейной системы. Преобразование
Лапласа имеет вид:
,
где Y(s)
и X(s)
соответственно преобразования Лапласа
для сигналов y(t)
на выходе и x(t)
на входе линейной системы. Преобразование
Лапласа имеет вид:
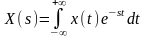 и
и
 .
.
Оригиналом передаточной функции H(s) является импульсная переходная функция или импульсная характеристика системы h(t). h(t) – выходной сигнал линейной системы как реакция на входной сигнал в виде дельта-функции (в цифровых системах входной сигнал для определения импульсной характеристики представляет собой простой импульс минимальной ширины (равной периоду квантования для дискретных систем) и максимальной амплитуды).
При подаче сигнала
на вход системы вначале возникает
нестационарный процесс установления
нового состояния (переходной процесс),
и действительная часть
 комплексной переменной
комплексной переменной
 входит в показатели экспонент, определяющих
затухающий (при
входит в показатели экспонент, определяющих
затухающий (при
 )
или возрастающий (при
)
или возрастающий (при
 )
характер переходного процесса. При этом
выражения с множителем, содержащим
экспоненту с
,
уменьшаются до нуля, следы нестационарности
процесса исчезают, и можно считать, что
во все последующее время
)
характер переходного процесса. При этом
выражения с множителем, содержащим
экспоненту с
,
уменьшаются до нуля, следы нестационарности
процесса исчезают, и можно считать, что
во все последующее время
 ,
и
,
и
 .
По этой причине амплитудно-частотную
и фазо-частотную характеристики (АФЧХ)
для линейной стационарной (
= 0)
системы можно получить из передаточной
функции путем формальной замены
комплексной переменной s =
.
По этой причине амплитудно-частотную
и фазо-частотную характеристики (АФЧХ)
для линейной стационарной (
= 0)
системы можно получить из передаточной
функции путем формальной замены
комплексной переменной s =  на
на
 .
Амплитудно-частотная
характеристика (АЧХ)
является зависимостью коэффициента
передачи линейной системы
от частоты; причём
АЧХ является
модулем
комплексной АФЧХ.
Фазо-частотная
характеристика (ФЧХ)
является зависимостью сдвига фазы между
входным и выходным сигналами от частоты,
и её можно получить как аргумент
комплексной АФЧХ.
Для удобства представления АЧХ и ФЧХ
изображают как правило в логарифмических
координатах (АЧХ – зависимость
.
Амплитудно-частотная
характеристика (АЧХ)
является зависимостью коэффициента
передачи линейной системы
от частоты; причём
АЧХ является
модулем
комплексной АФЧХ.
Фазо-частотная
характеристика (ФЧХ)
является зависимостью сдвига фазы между
входным и выходным сигналами от частоты,
и её можно получить как аргумент
комплексной АФЧХ.
Для удобства представления АЧХ и ФЧХ
изображают как правило в логарифмических
координатах (АЧХ – зависимость
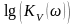 от
от
 ,
где
,
где
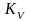 - действительный коэффициент передачи
сигнала, а ФЧХ – зависимость
- действительный коэффициент передачи
сигнала, а ФЧХ – зависимость
 от
).
от
).
