Тема 8. Основы статистической физики.

Распределение Максвелла: – функция распределения частиц по скоростям.

– плотность вероятности – определяет вероятность того, что скорость частицы имеет значение в интервале от до . Иначе, , где - число частиц, скорости которых имеют значение в интервале от до , N - полное число частиц.

, где – относительная скорость. Назначение функции распределения – определять средние величины по коллективу:

Средняя скорость .

Среднеквадратичная скорость

.

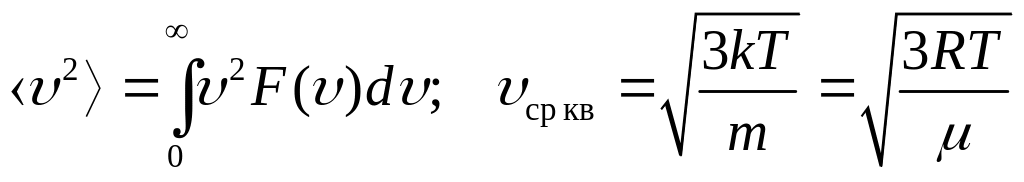Наиболее вероятная скорость .

Распределение Больцмана (распределение частиц в силовом поле) , где mgh – потенциальная энергия частиц в гравитационном поле. Данное распределение справедливо только для изотермической атмосферы, т.е. для T = const.

Задание по теме.

Ситуация. Температура воздуха 27°С.

Найти:

1. Наиболее вероятную скорость молекул а) азота; б) кислорода.

2. Среднюю арифметическую скорость молекул.

3. Среднеквадратичную скорость молекул.

4. Во сколько раз скорости молекул азота отличаются от скоростей молекул кислорода?

5. Какая часть молекул имеет скорости больше наиболее вероятной? Больше среднеквадратичной?

6. Какая часть молекул имеет скорости больше, чем наиболее вероятная на 1%?

7. Какая часть молекул имеет скорости, лежащие в интервале от 1,5 до 1,51 .

8. Во сколько раз количество молекул, скорость которых находится в интервале от 0,5 до 0,51 , отличается от количества молекул, скорость которых находится в интервале от 1,5 до 1,51 .

9. Во сколько раз отличается концентрация молекул на уровне моря и на горе высотой 1 км.

Тема 9. Явления переноса в газах.

Средняя длина свободного пробега – расстояние, которое проходит молекула между двумя последовательными соударениями. . Здесь d – эффективный диаметр молекулы (минимальное расстояние, на которое могут приблизиться две молекулы), n – концентрация молекул.

Среднее число соударений молекулы в единицу времени .

Явления переноса – процессы, связанные с восстановлением равновесия в термодинамической системе. Эти процессы связаны с неоднородностью одного из параметров:

плотности (концентрации) – диффузия или массоперенос, температуры – теплопроводность,

скорости направленного движения – вязкость (перенос импульса частиц в направлении перпендикулярном основному потоку).

Процессы характеризуются параметром, который называется поток – количество соответствующей величины, проходящее в единицу времени через какую-либо воображаемую поверхность площадью S.

Уравнение диффузии (Фика): , где коэффициент диффузии .

Уравнение теплопроводности (Фурье): .

Коэффициент теплопроводности , где – плотность газа, – удельная теплоемкость при постоянном объеме.

Сила трения между слоями газа, движущимися направленно со скоростью и (закон Ньютона) , где коэффициент динамической вязкости , z – направление, вдоль которого рассматривается изменение скорости потоков.

Задание по теме.

Воздух находится при нормальных условиях в оконном стеклопакете (площадь окна 2м², расстояние между стеклами 10см). Для молекул а) азота; б) кислорода; в) воды

Найти:

1. Среднюю арифметическую скорость молекул.

2. Среднюю длину свободного пробега молекул.

3. Коэффициент диффузии.

4. Коэффициент вязкости.

5. Коэффициент теплопроводности.

6. Установить зависимость коэффициентов от температуры и давления.

7. Какое количество теплоты будет переноситься при данных условиях через боковую поверхность окна за 1 час, если внутри помещения 22°С, а на улице -13°С. Считать процесс стационарным. Учесть, что азота в воздухе больше, чем кислорода в 3 раза, а влажность 50%.

Таблица вариантов УИРС по модулю 3

«Молекулярная физика и термодинамика»

вариант	Задание по теме 7		Задание по теме 8	Задание по теме 9
		для п.6,7	вопросы
1	1	а)	1, 2, 3, 4, 9	а)
2	2	б)	1, 2, 3, 5, 9	б)
3	3	в)	1, 2, 3, 6, 9	в)
4	5	г)	1, 2, 3, 7, 9	а)
5	6	д)	1, 2, 3, 8, 9	б)
6	7	е)	1, 2, 3, 4, 9	в)
7	1	ж)	1, 2, 3, 5, 9	а)
8	2	а)	1, 2, 3, 6, 9	б)
9	3	б)	1, 2, 3, 7, 9	в)
10	5	в)	1, 2, 3, 8, 9	а)
11	6	г)	1, 2, 3, 4, 9	б)
12	7	д)	1, 2, 3, 5, 9	в)
13	1	е)	1, 2, 3, 6, 9	а)
14	2	ж)	1, 2, 3, 7, 9	б)
15	3	а)	1, 2, 3, 8, 9	в)
16	5	б)	1, 2, 3, 4, 9	а)
17	6	в)	1, 2, 3, 5, 9	б)
18	7	г)	1, 2, 3, 6, 9	в)
19	1	д)	1, 2, 3, 7, 9	а)
20	2	е)	1, 2, 3, 8, 9	б)

1 Коэффициент восстановления к численно равен относительной скорости тел после удара к относительной скорости тел до удара.

56