Тема 7. Молекулярная физика и термодинамика.

Количество вещества – физическая величина, характеризующая количество однотипных структурных единиц, содержащихся в веществе. 1 моль (ν) вещества содержит моль^-1 (постоянная Авогадро) структурных единиц .

Идеальный газ – физическая модель газа, размерами и взаимодействием молекул которого можно пренебречь.

Уравнение состояния идеального газа (Менделеева-Клапей-рона) , где R = 8,31Дж/моль^.К – универсальная газовая постоянная, или , где Дж/К – постоянная Больцмана .

Уравнение состояния реального газа (Ван-дер-Ваальса) 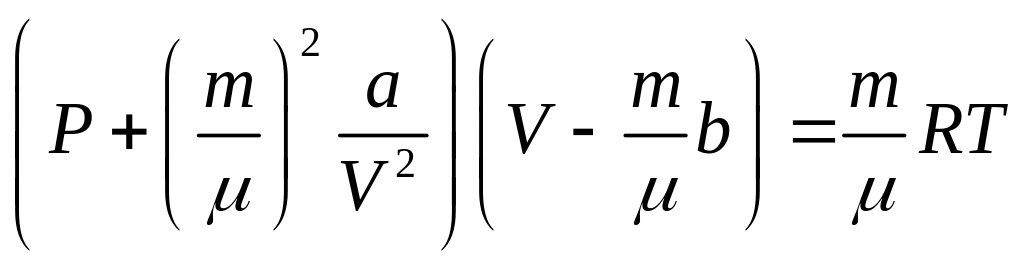, где – собственный объём молекул одного моля, а – коэффициент зависящий от природы газа и определяющий взаимодействие молекул.

Основное уравнение молекулярно-кинетической теории

, где Е – энергия молекул газа.

На одну степень свободы молекулы приходится энергия ε = ½ kT.

Число степеней свободы ( i ) – количество независимых координат, описывающих движение молекул.

Для одноатомных молекул i = 3 (поступательные степени свободы), для двухатомных i = 5 (3 поступательных + 2 вращательные), для трехатомных и многоатомных i = 6 ( 3 поступательных + 3 вращательных).

Внутренняя энергия идеального газа .

Изменение внутренней энергии связано только с изменением температуры .

Внутренняя энергия реального газа , где – теплоемкость идеального газа при постоянном давлении.

Работа газа .

Первое начало термодинамики : теплота, сообщаемая системе, расходуется на изменение внутренней энергии системы и на совершение системой работы против внешних сил.

Теплоемкость – величина, численно равная количеству тепла, которое нужно сообщить телу, чтобы повысить его температуру на 1К .

Удельная теплоемкость – величина, численно равная количеству тепла, которое нужно сообщить единице массы тела, чтобы повысить его температуру на 1К .

Молярная теплоемкость – величина, численно равная количеству тепла, которое нужно сообщить молю вещества, чтобы повысить его температуру на 1К .

Адиабатический процесс – процесс, протекающий без теплообмена с внешней средой , т.е. и .

Уравнение адиабатического процесса (уравнение Пуассона) , , где – показатель адиабаты.

Изопроцесс	уравнение	I -ое начало	работа	молярная теплоемкость
Изотермический T=const	P2V2=P1V1	Q = A		∞
Изобарический P=const		Q = ΔU + A	P(V2-V1)
Изохорный V=const		Q = ΔU	0
Адиабатический		Q = 0	Α = –ΔU =	0

Второе начало термодинамики. Наиболее часто встречаются формулировки:

– невозможен процесс, единственным результатом которого является превращение всей теплоты, полученной от нагревателя в эквивалентную ей работу.

– невозможен процесс, единственным результатом которого является передача энергии в форме теплоты от холодного тела к горячему.

– энтропия замкнутой системы при любых происходящих в ней процессах не может убывать (здесь – энтропия системы, – термодинамическая вероятность состояния), в итоге еще одна формулировка:

– термодинамическая вероятность состояния замкнутой системы при всех происходящих в ней процессах не может убывать .

Изменение энтропии или .

Коэффициент полезного действия теплового двигателя , где А – работа, совершенная в цикле, – количество теплоты, полученное от нагревателя, – количество теплоты отданное охладителю.

Кпд цикла Карно . – температура нагревателя, – температура охладителя (холодильника).

Теоремы Карно    1. Коэффициент полезного действия любой обратимой тепловой машины, не зависит от природы рабочего тела и устройства машины, а является функцией только температуры нагревателя и холодильника:     

     2. Коэффициент полезного действия любой тепловой машины, работающей по необратимому циклу, меньше коэффициента полезного действия машины с обратимым циклом Карно, при условии равенства температур их нагревателей и холодильников: .

Коэффициент полезного действия или холодильный коэффициент холодильной машины можно определить как отношение отнятой от охлаждаемого тела теплоты к затраченной для этого механической работе А: . – количество теплоты переданное тепловому резервуару.

Задание по теме.

В сосуде объёмом V₁ = 6 л при давлении Р₁= 0,4 МПа находится один моль двухатомного газа, который затем совершает замкнутый цикл, состоящий из последовательных процессов (согласно таблице вариантов).

вариант	1-2	2-3	3-4	4-1
1	Изобара V2=3V1	Изотерма V3=1,5V2	Изобара до Т3=Т1	изотерма
2	Изобара V2=3V1	Изотерма V3=1,5V2	Изохора до Т3=Т1	изотерма
3	Изобара V2=3V1	Адиабата V3=1,5V2	Изобара до V3=V1	изохора
4 (пример)	Изотерма V2=4V1	Изохора Р3=3Р2	Изотерма до Р4=Р1	изобара

	1-2	2-3	3-1	----
5	Изобара Т2=2Т1	Изохора Т=Т1	Изотерма	----
6	Изохора Р2=2Р1	Изотерма Р3=Р1	Изобара	----
7	Адиабата V2=1,5V1	Изобара Т=Т1	Изотерма	----

1. Найти параметры точек 2, 3 и 4. Изобразить цикл в координатах: Р, V ; V, Т и Р, Т .

2. Найти количество теплоты Q, поглощенное в цикле.

3. Найти количество теплоты Q, выделенное газом в цикле.

4. Найти работу, совершенную газом в цикле.

5. Найти кпд цикла.

6. Найти изменение внутренней энергии ΔU при переходе а) 1-2; б) 2-3; в) 3-4; г) 1-3; д) 2-4; е) 4-1; ж) 3-1 .

7. Найти изменение энтропии ΔS в процессе а) 1-2;

б) 2-3; в) 3-4; г) 1-3; д) 2-4; е) 4-1; ж) 3-1 .

Пример решения варианта 4.

Температура начального состояния по уравнению Менделеева-Клапейрона .

Уравнение изотермического процесса 1-2:

, откуда .

Уравнение изохорического процесса 2-3:

, откуда .

Уравнение изотермического процесса 3-4:

, откуда .

точка	P , 106 Па	V , 103 м3	T , К
1	0,4	6	290
2	0,1	24	290
3	0,3	24	870
4	0,4	18	870

Для упрощения дальнейших расчетов составим таблицу параметров характерных точек.

Нанесем эти точки на оси и построим графики процессов.

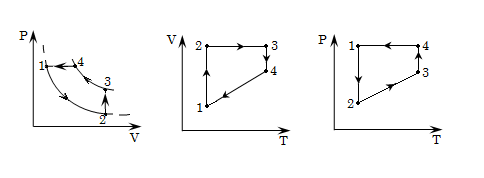
Теплота поглощенная или выделенная в процессах:

1-2 изотермический

;

3. изохорический

;

3-4 изотермический

;

4-1 изобарический

В процессах 1-2 и 2-3 теплота положительная, следовательно, шло её поглощение от нагревателя. В процессах 3-4 и 4-1 – отрицательная, следовательно, система отдает теплоту охладителю. Тогда отвечая на вопрос 2:

.

Отвечая на вопрос 3:

.

4. Так как цикл замкнутый, изменение внутренней энергии , тогда работа в цикле

.

5. Работа в цикле отрицательная, а это значит, что такой цикл обратный (на это указывает и направление процесса в параметрах ). В этом случае цикл соответствует холодильной машине, для которой определяется холодильный коэффициент: . (В отличие от кпд теплового двигателя кпд холодильной машины может быть больше 1).

6. Изменение внутренней энергии в процессах находим по определению: .

7. Изменение энтропии идеального газа

В соответствии с этой формулой изменение энтропии в процессе 1-2 .

В процессе 2-3 . Так как энтропия является термодинамическим потенциалом, то для процесса 1-3

.