1. Угловую скорость ω движения, угловое ускорение ε через 2с после начала движения.

2. Тангенциальное и нормальное ускорения через 2с после начала движения.

3. Изменение тангенциального ускорения за единицу времени.

4. Полное ускорение в момент времени t = 2с.

5. Угол, составляемый вектором полного ускорения с радиусом колеса в момент t = 2с.

Задача 2. Однородный диск радиусом R = 0,2м и массой m = 5кг вращается вокруг оси, проходящей через его центр перпендикулярно к его плоскости. Зависимость углового перемещения дается уравнением а) φ = 6t + 0,05t² , рад.

б) φ = 5t² – 0,1 t, рад.

Найти:

1. Момент инерции диска.

2. Частоту вращения диска через 5с.

3. Угловое ускорение.

4. Касательную силу F , приложенную к ободу диска.

5. Момент сил торможения, если через t₁ = 10с от начала движения касательная сила перестала действовать, а диск остановился за t₂ = 20с.

Задания по теме.

Ситуация 1. а) колесо; б) диск; в) шар массой m = 4 кг радиусом R = 0,5м вращаясь равнозамедленно уменьшило за время t = 1мин частоту вращения от п₁ = 300об/мин до п₂ = 180об/мин.

Найти:

1. Угловое ускорение ε колеса (диска, шара).

2. Момент инерции колеса (диска, шара).

3. Момент сил торможения М.

4. Время до полной остановки.

5. Число оборотов N, сделанных колесом (диском, шаром) до остановки.

Ситуация 2. Две гири с массами т₁ = 2кг и т₂ = 1,5кг связаны невесомой нерастяжимой нитью и перекинуты через блок массой т = 0,5кг и радиусом R = 5см (рис 1-4). Коэффициент трения гири 2 о поверхность μ = 0,1.

Найти:

силу натяжения Т₁ и Т₂ нитей и ускорение а, с которым движутся гири, если а) трение в блоке отсутствует; б) при вращении действует момент сил трения М_тр = 0,049Н∙м.

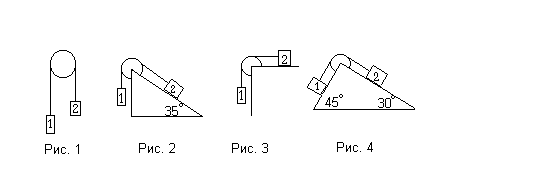
Алгоритм решения задачи.

В данной задаче система 3-х движущихся тел, поэтому для каждого из них записывают уравнения движения (2-ой закон Ньютона для поступательного движения грузов и основное уравнение вращательного движения для блока).

Н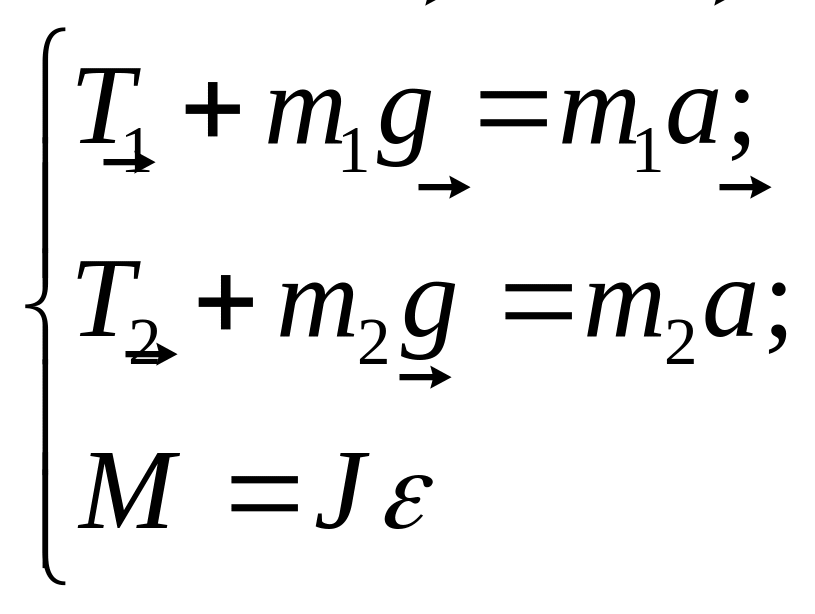 апример, для рис.1:

Для записи в скалярной форме данных уравнений, выбирают оси, совпадающие с направлением движения грузов.

На блок действуют силы натяжения Т₁ и Т₂, тогда момент этих сил, действующих на блок М=(Т₂ – Т₁)R (знак момента движущей силы положительный, тормозящей – отрицательный).

Связь линейного и углового ускорения ε = a/R. Далее решают систему уравнений относительно неизвестных.

Тема 4. Законы сохранения энергии, импульса,

момента импульса.

Закон сохранения импульса: импульс замкнутой системы не меняется с течением времени. Иначе, при любых процессах, происходящих в замкнутой системе, скорость её центра инерции сохраняется неизменной .

Закон сохранения момента импульса системы материальных точек: если результирующий момент всех внешних сил, приложенных к системе, относительно какой-либо неподвижной оси тождественно равен нулю, то момент импульса системы относительно той же оси не изменяется с течением времени:

.

Работа – количественная характеристика изменения механического движения тела в процессе силового взаимодействия. При перемещении из т.1 в т.2

, или .

Мощность – скорость совершения работы: .

Энергия – скалярная физическая величина, являющаяся единой мерой различных форм движения материи и мерой перехода движения материи из одних форм в другие.

Кинетическая энергия ( ) – мера механического движения тела, определяется той работой, которую может совершить тело в процессе своего торможения.

При поступательном движении .

При вращательном движении .

Полная кинетическая энергия .

Если работа при перемещении из т.1 в т.2 не зависит от формы траектории, то силу, под действием которой совершается перемещение, называют консервативной. В этом случае тело в поле таких сил обладает потенциальной энергией, и работа консервативных сил совершается за счет убыли потенциальной энергии тела .

Для консервативных сил характерно: .

Потенциальная энергия гравитационного взаимодействия:

, где r – расстояние между центрами масс, G = 6,673 ·10^-11 м³кг^-1с^-2 – гравитационная постоянная.

Потенциальная энергия в поле тяготения Земли вблизи поверхности приближённо выражается формулой: ,

где m – масса тела, g – ускорение свободного падения, h – высота положения центра масс тела над произвольно выбранным нулевым уровнем.

Потенциальная энергия упруго деформированного тела: , где х – абсолютная деформация, k – коэффициент упругости (жесткость), зависящий от размеров и материала тела.

Полная механическая энергия замкнутой системы тел:

.

Консервативная система – система тел, внутренние силы взаимодействия между которыми консервативны, а все внешние силы стационарны и консервативны.

Диссипативные силы – силы трения и сопротивления – уменьшают полную механическую энергию системы и преобразуют её во внутреннюю энергию тел.

Закон сохранения механической энергии: полная механическая энергия консервативной системы не изменяется с течением времени.

Общефизический закон сохранения энергии: в замкнутой системе энергия может переходить из одних видов в другие и передаваться от одного тела к другому, но её общее количество остается неизменным.

Задания по теме.

Ситуация 1-А. Тело массой т = 1 кг брошено со скоростью υ₀ = 15 м/с вертикально вверх а) с земли; б) с уровня Н = 10 м.

Ситуация 1-Б. Тело массой т = 1 кг брошено с высоты Н=50м со скоростью υ₀ = 15 м/с горизонтально.

Ситуация 1-В. Тело массой т = 1 кг брошено со скоростью υ₀ = 15 м/с с высоты Н=50м под углом α = 30° к горизонту.

Найти:

1. Полную энергию тела.

2. Зависимость кинетической энергии от времени.

3. Кинетическую энергию тела через t = 1 с.

4. Зависимость потенциальной энергии от времени.

5. Потенциальную энергию тела через t = 1 с.

6. Время, когда кинетическая энергия тела равна потенциальной энергии.

7. На какой высоте кинетическая энергия тела равна потенциальной энергии.

Ситуация 2-А. Тело массой 0,5 кг, которое двигалось по горизонтальному участку со скоростью υ₀ = 15 м/с, начинает подниматься по инерции на наклонную плоскость, угол наклона которой 30°. Коэффициент трения μ = 0,1.

Ситуация 2-Б. Однородному а) цилиндру б) кольцу (массой т = 1кг, радиусом R = 0,1м), находящемуся у основания наклонной плоскости, сообщают начальный импульс. В результате он начинает катиться без скольжения вверх со скоростью υ₀ = 3м/с. Плоскость образует с горизонтом угол α = 20°. При движении действует постоянный по модулю момент силы трения качения М_тр = 0,1Н·м.

Найти:

1. Механическую энергию тела (цилиндра, кольца) в начальный момент времени.

2. Какой путь пройдет тело (цилиндр, кольцо) по наклонной поверхности, если трение отсутствует.

3. Какой путь пройдет тело (цилиндр, кольцо) до остановки по наклонной поверхности с учетом трения.

4. Количество теплоты, выделенное при трении на пути движения вверх.

5. С какой скоростью тело при скатывании вниз вернется к основанию наклона.

6. Какой путь после скатывания пройдет тело до остановки.

Ситуация 3. Под действием силы тяжести груза массой 500г пружина растягивается на 10см.

Найти:

1. Работу А, которую нужно совершить, чтобы сжать пружину на х = 5см.

2. Работу А_д, которую нужно совершить, чтобы сжать пружину еще на 5см.

3. На какую высоту подскочит шарик массой 100г, лежащий на вертикально расположенной, сжатой на 10см пружине, если её отпустить.

Алгоритм решения задач на закон сохранения энергии.

1. Выясните из условия, является ли замкнутая система тел консервативной или нет (т.е. ответьте на вопрос, действуют ли силы трения или сопротивления).

2. Определите полную механическую энергию системы в начальный момент времени.

3. Определите полную механическую энергию системы в конечный момент времени и приравняйте её полной энергии в начальный момент времени при условии, что система консервативная. Далее решайте уравнение относительно неизвестного.

4. Если система неконсервативная, то работа сил трения (теплота, выделившаяся в результате трения) прибавляется к механической энергии в конечный момент времени.

5. Если система незамкнутая или действует сила тяги, то работа этих сил изменяет кинетическую энергию и, следовательно, полную механическую энергию системы.

Ситуация 4-А. На рельсах стоит платформа массой т₁ = 10т. На платформе закреплено орудие массой т₂ = 5т, из которого производится выстрел а) вдоль рельсов; б) под углом 30° к горизонту. Масса снаряда т₃ = 100кг, его начальная скорость относительно орудия υ ₀ = 500м/с.

Ситуация 4-Б. Платформа двигалась со скоростью υ = 9км/час и выстрел произведен по направлению движения.

Ситуация 4-В. Платформа двигалась со скоростью υ = 9км/час и выстрел произведен против направления движения.

Найти:

1. Скорость платформы в первый момент после выстрела.

2. Путь, который пройдет платформа до остановки, если коэффициент трения движению μ = 0,05.

3. Энергию порохового заряда.

Ситуация 5-А. Тело массой т₁ = 1кг движется со скоростью υ₁ = 3м/с; тело массой т₂ = 1,5кг покоится.

Ситуация 5-Б. Тело массой т₁ = 1кг движется со скоростью υ₁ = 3м/с; тело массой т₂ = 1,5кг движется со скоростью υ₂ = 2м/с а) в том же направлении, что и тело 1; б) навстречу.

Ситуация 5-В. Тело массой т₁ = 1кг движется со скоростью υ₁ = 3м/с; тело массой т₂ = 1,5кг движется под углом 30° к скорости первого тела.

Считая удар центральным и а) упругим; б) неупругим;

в) частично упругим с коэффициентом восстановления¹ к= 0,8

найти:

1. Скорость тел и₁ и и₂ после удара.

2. Количество теплоты, выделившееся при ударе.

Алгоритм решения задач на закон сохранения импульса.

1. Выберите систему координат, относительно которой будете записывать уравнение.

2. В данной системе координат определите по условию импульсы всех тел, включенных в замкнутую систему в начальный момент времени (до какого-либо взаимодействия); запишите их сумму, учитывая знаки проекций скоростей тел на оси системы координат.

3. Аналогично запишите сумму импульсов тел после взаимодействия. Если из условия Вы не можете однозначно определить направление движения после взаимодействия одного из тел, примите его скорость положительной. Тогда в случае, если Вы не угадали направления его движения, значение скорости будет с отрицательным знаком.

4. Приравняйте импульс до взаимодействия импульсу после взаимодействия.

5. Если этого уравнения не достаточно для решения задачи, запишите уравнение закона сохранения энергии по тому же принципу: сумма кинетических энергий тел до взаимодействия равна сумме кинетических энергий тел после взаимодействия (в случае абсолютных ударов); или сумма кинетических энергий тел до взаимодействия равна сумме кинетических энергий тел после взаимодействия и энергии деформации (в случае неабсолютных ударов).

Ситуация 6. Горизонтальная платформа массой т = 100кг и радиусом R = 1,5м вращается вокруг вертикальной оси, проходящей через центр платформы, с частотой n₁ = 4об/мин. Человек массой m₀ = 60кг стоит при этом на краю платформы.

Найти:

1. С какой частотой n₂ будет вращаться платформа, если

А) человек перейдет от края платформы на 1 м ближе к центру;

Б) человек перейдет от края платформы в её центр;

В) человек пойдет по краю платформы в направлении её вращения со скоростью υ = 2м/с;

Г) человек пойдет по краю платформы против направления её вращения с υ = 2м/с;

Д) человек бросит гирю массой m = 2кг со скоростью υ = 20м/с по касательной к платформе против направления вращения.

2. Какую работу совершит при этом человек.

Алгоритм решения задач на закон сохранения момента импульса.

1. Выберите систему отсчета, относительно которой будете определять моменты импульсов тел.

2. В соответствии с условием определите момент импульса системы в начальный момент времени. Для этого может понадобиться найти момент инерции тел, относительно оси вращения.

3. Запишите момент импульса системы тел после взаимодействия. Учтите, что чаще всего, изменение момента импульса происходит вследствие изменения момента инерции, поэтому не забудьте найти момент инерции после взаимодействия.

4. Приравняйте момент импульса системы до взаимодействия тел к моменту импульса после взаимодействия.

П ример решения задачи 6 -А вопрос 1, 2.

Человек и платформа образуют замкнутую систему тел, поэтому можно использовать закон сохранения момента импульса. В начальный момент времени момент импульса системы складывался из момента импульса человека

и момента импульса платформы .

В результате перемещения человека его момент инерции изменился , следовательно, изменился и момент инерции всей системы. В итоге по закону сохранения момента импульса

, откуда частота вращения платформы будет:

Работа человека А будет равна изменению кинетической энергии системы:

, где – кинетическая энергия вращательного движения.

Подставим: Вычислим: Ответ:

Таблица вариантов УИРС по модулю 1

«Механическое движение»

Вари-ант	Задание по теме 1	Задание по теме 2	Задание по теме 3	Задание по теме 4
1	Задача 2а)	Сит.1	Задача 1а)	1-А а)	6-А
2	Задача 2б)	Сит.4	Задача 1б)	1-А б)	6-Б
3	Задача 3а)	Сит.5	Задача 2б)	1-Б	6-В
4	Задача 3б)	Сит.3-Б а)	Задача 2а)	1-В	6-Г
5	сит.1	Задача 1б)	Сит.1 а)	2-А	6-Д
6	сит.2	Задача 1а)	Сит.1 б)	2-Б а)	4-А а)
7	сит.3	Задача 2б)	Сит.1 в)	2-Б б)	4-А б)
8	сит.4	Задача 2а)	Сит.2 р.1	3	4Б
9	Задача 2а)	Сит.2 а)	Сит.2 р.2	1-А а)	4В
10	Задача 2б)	Сит.2 б)	Сит.2 р.3	1-А б)	5-А
11	Задача 3а)	Сит.2 в)	Сит.2 р.4	1-Б	5-Б а)
12	Задача 3б)	Сит.2 г)	Задача 1а)	1-В	5-Б б)
13	сит.1	Сит.2 д)	Задача 1б)	2-А	5В
14	сит.2	Сит.2 е)	Задача 2б)	2-Б а)	6-В
15	сит.3	Сит.3-А р.1	Задача 2а)	2-Б б)	6-Г
16	сит.4	Сит.3-А р.2	Сит.1 а)	3	6-Д
17	Задача 1а)	Сит.3-А р.3	Сит.1 б)	1-В	4-А а)
18	Задача 1б)	Сит.3-А р.4	Сит.1 в)	2-А	4-А б)
19	Задача 2б)	Сит.3-Б б)	Сит.2 р.1	2-Б а)	6-А
20	Задача 3а)	Сит.3-Б в)	Сит.2 р.2	2-Б б)	6-Б