Тема 2. Динамика поступательного движения.

Сила – векторная величина являющаяся мерой взаимодействия материальных тел.

Инерция – свойство тел сохранять покой или равномерное прямолинейное движение, иначе – противиться изменению своего состояния.

Масса – мера инертности тел.

Закон инерции (1-ый закон Ньютона): Всякое тело сохраняет состояние покоя или равномерного прямолинейного движения до тех пор, пока воздействие со стороны других тел не заставит его изменить это состояние.

Из 1-го закона вытекает возможность существования инерциальных систем отсчета (ИСО), в которых, если на тело не действуют другие тела, оно либо покоится, либо движется равномерно и прямолинейно. Иначе, прямолинейное равномерное движение не требует для своего поддержания никакого воздействия.

Количество движения (импульс): .

2-ой закон Ньютона: изменение количества движения за любой бесконечно малый промежуток времени равно элементарному импульсу силы .

Если масса тела не изменяется, то согласно принципу независимости действия сил,

, где – силы, действующие на тело.

3-ий закон Ньютона: Силы, с которыми действуют друг на друга взаимодействующие тела, равны по величине и противоположны по направлению.

Динамическое уравнение движения: дифференциальное уравнение 2-го порядка , из которого при известных начальных условиях и можно получить кинематическое уравнение движения .

Механическая система: совокупность материальных точек (тел), находящихся во взаимодействии, согласно 3-ему закону Ньютона.

Центр инерции системы: такая точка внутри системы, радиус-вектор которой .

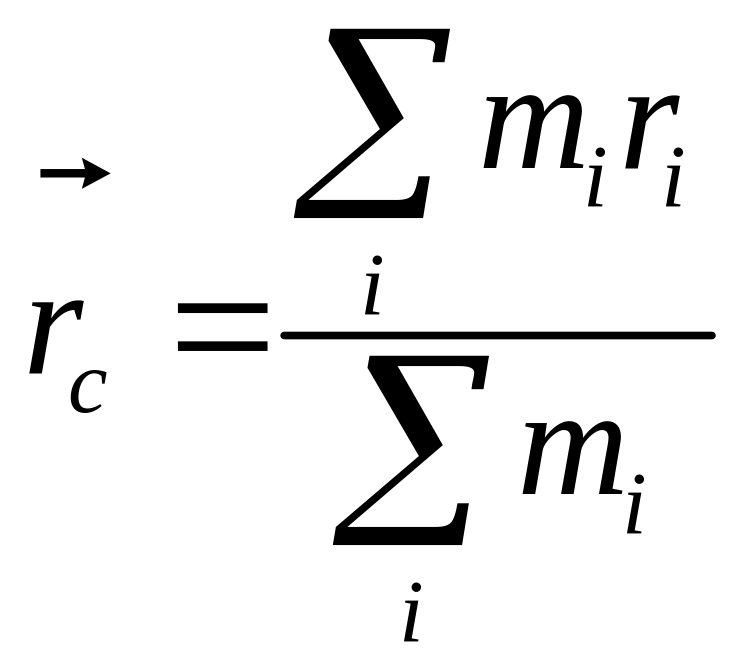Для тел правильной формы эта точка совпадает с геометрическим центром.

Теорема о движении центра инерции: центр инерции механической системы движется как материальная точка, масса которой равна массе всей системы и на которую действует сила, равная главному вектору внешних сил, приложенных к системе .

Замкнутая механическая система: если на неё не действуют внешние силы, или главный вектор внешних сил тождественно равен нулю.

Закон сохранения импульса: импульс замкнутой системы не меняется с течением времени. Иначе, при любых процессах, происходящих в замкнутой системе, скорость её центра инерции сохраняется неизменной. .

Данный закон является следствием однородности пространства: параллельный перенос в нём замкнутой системы как целого не должен отражаться на физических свойствах системы и законах её движения.

Силы в механике :

Сила гравитационного взаимодействия .

Сила тяжести – направлена к центру Земли.

Сила реакции опоры (направлена перпендикулярно поверхности) или натяжения нити . Согласно 3-ему закону Ньютона эти силы являются силами противодействия со стороны опоры или подвеса.

Сила трения скольжения направлена противоположно движению тела.

Сила упругости (закон Гука) (х – абсолютная деформация тела).

Сила тяги – определена некоторым устройством и источником энергии (рабочим телом и количеством теплоты, которое можно преобразовать в полезную работу).

Вес тела – сила, с которой тело действует на опору или подвес или .

Задачи на определения.

Задача 1. Задано кинематическое уравнение движения тела массой 100г : а) , м.

б) , м.

Найти:

1. Уравнение действующей силы .

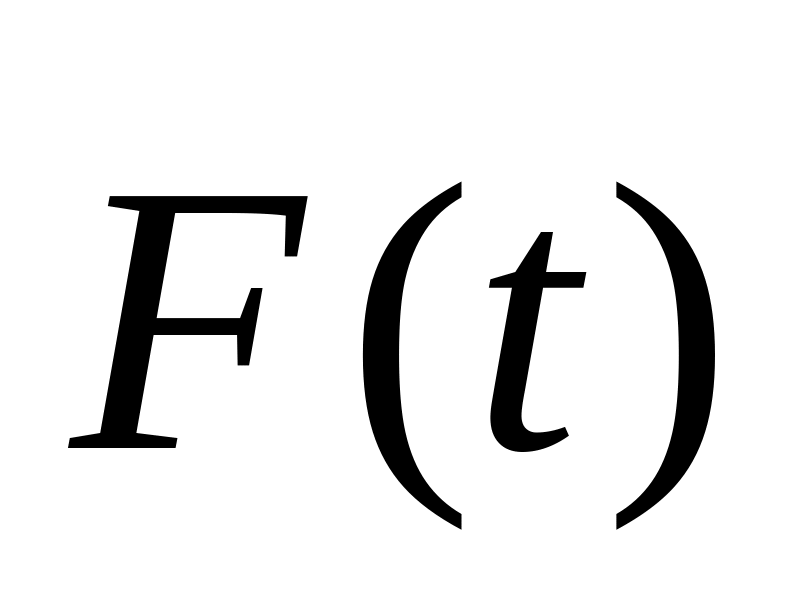2. Направление и значение силы в момент времени t = 5с.

3. Изменение импульса тела за 5-ую секунду движения.

Задача 2. На покоящееся тело массой 100г, находящееся в точке с координатами (0, 3, -5), начинает действовать сила а) , Н. б) , Н.

Найти:

1. Закон изменения скорости тела .

2. Кинематическое уравнение движения .

3. Изменение импульса тела за 5-ую секунду движения.

Задания по теме.

Ситуация 1. Автомобиль массой т = 1 т двигался со скоростью υ = 72 км/час, когда выключили двигатель. Коэффициент трения колес о дорогу μ = 0,1.

Найти:

1. Ускорение замедленного движения.

2. Какой путь автомобиль пройдет до остановки.

3. Время движения до остановки.

4. Какова должна быть сила тяги, чтобы вновь развить такую же скорость за 1 минуту?

Ситуация 2. Брусок массой т = 200 г находится на наклонной плоскости, составляющей с горизонтом угол α =30º.

Найти:

а) При каком предельном значении коэффициента трения тело начнет скользить вниз.

б) Какую силу нужно приложить к телу, чтобы оно покоилось, если коэффициент трения μ = 0,1.

в) Какую силу нужно приложить к телу, чтобы оно двигалось равномерно вверх, если коэффициент трения μ = 0,1.

г) Какую силу нужно приложить к телу, чтобы оно двигалось равномерно вниз, если коэффициент трения μ = 0,1.

д) Какую силу нужно приложить к телу, чтобы оно двигалось равноускоренно вверх с ускорением а = 0,2м/с², если коэффициент трения μ = 0,1.

е) Какую силу нужно приложить к телу, чтобы оно двигалось равноускоренно вниз с ускорением а = 0,2м/с², если коэффициент трения μ = 0,1.

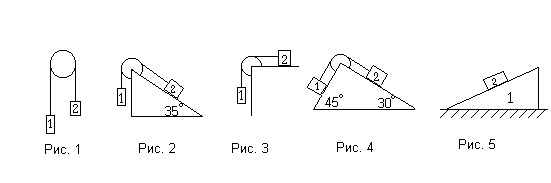
Ситуация 3-А. Две гири с массами т₁ = 2кг и т₂ = 1,5кг связаны невесомой нерастяжимой нитью и перекинуты через невесомый блок (рис 1–4). Коэффициент трения гирь о поверхность μ = 0,1. Трение в блоке отсутствует. Определить силу натяжения нити Т и ускорение а, с которым движутся гири.

Ситуация 3-Б*. По рис. 2 и 4, найти отношение масс тел т₂/т₁ при котором тело 2 :

а) будет опускаться; б) будет подниматься;

в) останется в покое.

Ситуация 4. Лифт начинает (заканчивает) движение вверх (вниз) с ускорением 0,2м/с². Найти в этот момент вес пассажира, масса которого 80кг.

Ситуация 5. Самолет делает «мертвую петлю» радиусом R = 500 м с постоянной скоростью υ = 360км/час. Найти вес летчика, масса которого т = 80 кг, в верхней, нижней, средней точках петли.

Алгоритм решения задач по динамике.

1. В соответствии с условием схематически нарисуйте движущееся тело.

2. Обозначьте все силы, действующие на тело. Точка приложения сил – центр инерции.

3. Выберите систему координат, начало которой совпадает с центром инерции, ось Ох – с направлением движения, Оу – перпендикулярная Ох.

4. Если направление силы не совпадает с направлением выбранных осей, определите проекции силы на оси.

5. Запишите уравнение 2-го закона Ньютона в векторном виде и в проекциях на оси координат. Если сила по направлению не совпадает с осью координат, её пишут со знаком минус.

Пример: движение тела вверх с ускорением по наклонной плоскости. Основное уравнение в векторной форме:

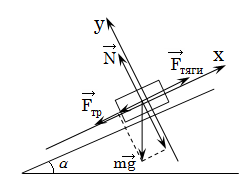
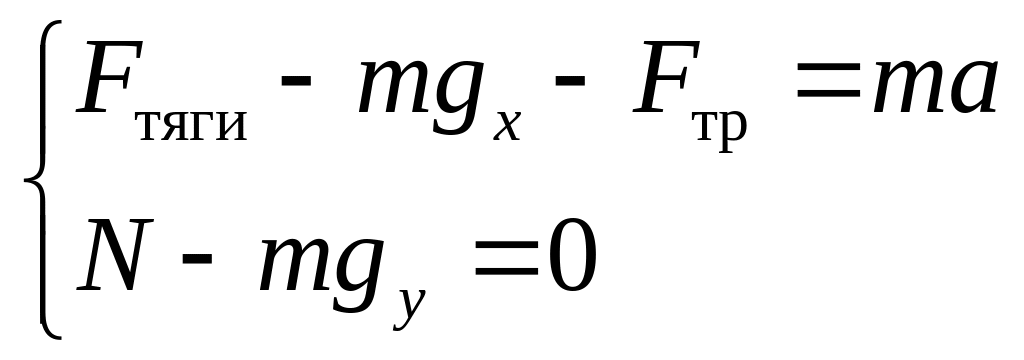
Из второго уравнения

.

Сила трения

.

Далее можно из этих уравнений находить неизвестные согласно условию.

• Если тело покоится на наклонной плоскости, то сила трения направлена против проекции силы тяжести на направление возможного движения.

• Учтите, что для горизонтальной плоскости можно пользоваться этими же уравнениями, только α = 0º.

• Если движутся тела, связанные в систему, то уравнение движения записывается для каждого из тел. Связывать эти уравнения будет только сила натяжения сцепки (внутренняя сила взаимодействия), приложенная к каждому из тел. Оси координат и их направление для каждого тела могут быть при этом независимыми друг от друга.