
- •Тригонометрические функции. Преобразования тригонометрических выражений Пособие для учащихся 11 класса
- •От автора
- •Введение
- •П. 2. Формулы перевода углов из градусной меры в радианную, и наоборот
- •П. 3. Определение тригонометрических функций
- •П. 4. Таблица значений тригонометрических функций
- •П. 5. Свойства тригонометрических функций
- •П. 6. Азбука тригонометрии
- •П. 7. Нахождение значений тригонометрических функций
- •Линия котангинса
- •П. 12. Преобразования графиков
- •П. 13. Обратные тригонометрические функции
- •П. 14. Простейшие тригонометрические уравнения
- •П. 15. Простейшие тригонометрические неравенства
- •П. 17. Формулы приведения и их применение
- •П. 18. Формулы двойного и половинного угла
- •П. 19. Формулы суммы и разности тригонометрических функций
- •III зачетный раздел Тригонометрические уравнения п. 20. Методы решения тригонометрических уравнений
- •Упрощение уравнения, используя тригонометрические формулы.
- •II. Метод введения новой переменной
- •III. Однородные тригонометрические уравнения.
- •Алгоритм отыскания производной функции :
- •Правила дифференцирования
- •П. 22. Применение производной
- •Физический смысл производной.
- •Геометрический смысл производной.
- •Алгоритм составления уравнения касательной к графику функции:
- •III. Исследование функции на монотонность и экстремум.
- •IV. Применение производной к построению графика функции.
- •V. Отыскание наибольшего и наименьшего значений непрерывной функции на отрезке .
- •Справочный раздел
- •Ответы, указания, решения
- •Литература
- •Содержание
- •Тригонометрические функции. Преобразование тригонометрических выражений
- •Г. Новокузнецк, ул.Транспортная, 17
III зачетный раздел Тригонометрические уравнения п. 20. Методы решения тригонометрических уравнений
Заметим, что каково бы ни было заданное тригонометрическое уравнение, существует только четыре вида уравнений, дающие решения – это простейшие тригонометрические уравнения, см. п.14.
Рассмотрим основные методы решения тригонометрических уравнений, позволяющие сводить их к простейшим.
Упрощение уравнения, используя тригонометрические формулы.
Пример 1.
Решите уравнение:
![]()
Преобразуем выражение и воспользуемся формулой (3) п. 16.
![]()
![]()
![]()
![]() — простейшее
тригонометрическое урвнение
— простейшее
тригонометрическое урвнение
![]()
![]()
![]() Ответ:
Ответ:
![]()
Пример 2.
Решите уравнение:
![]()
Используем Формулы приведения п. 17


Пример 3.
Решите уравнение:
![]()
Применим формулу (1) п. 18

Пример
4. Решите уравнение:
![]()



Ответ:
![]() ;
;
![]() .
.
Пример 5.
Решите уравнение:
![]()
Используя формулы приведения (п. 17),
заменим
![]() :
:
![]()
Применим формулу (1) п.18,
представим выражение в виде произведения:

![]()
![]()
![]()
![]()
Ответ:
![]()
Пример 6.
Решите уравнение:
![]()
Используя формулу
(1) п. 6, заменим
![]() на 1.
на 1.

Ответ:
Пример 7.
Решите уравнение:
![]()
Сгруппируем слагаемые так, чтобы получились формулы: суммы и двойного аргумента.
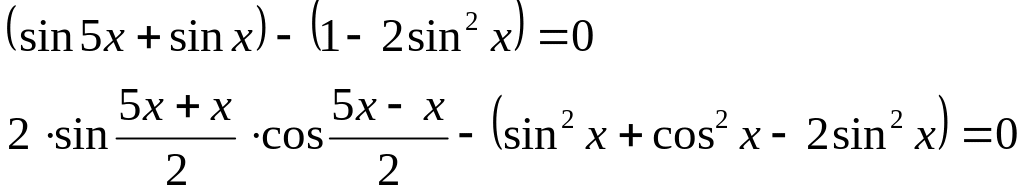
![]()
![]()
Вынеся
![]() общим множителем,
общим множителем,
получим два простейших уравнения:
![]()
![]()


Ответ:
![]() ;
;
![]() .
.
II. Метод введения новой переменной
Очень часто тригонометрическое уравнение по внешнему виду напоминает квадратное уравнение. Выполнив в уравнении соответствующую замену переменной, можно легко найти его решение.
Пример 8.
Решите уравнение:
![]()
Замена
![]()


Обратная замена:
![]()
![]()
![]()
Ответ:![]() ;
;
![]() .
.
В некоторых уравнениях требуется сделать дополнительное преобразование, чтобы уравнение свелось к квадратному:
Пример 9.
Решите уравнение:
![]()
Заменим, используя
формулу (1) п. 6,
![]()
![]()
![]()
Замена:
![]()
![]()
Решив уравнение,
найдем
![]()
Обратная замена:
![]() - уравнение не
имеет решения,
- уравнение не
имеет решения,
![]() т.к.
т.к.
![]()
Ответ:
![]() .
.
Пример 10.
Решите уравнение:
![]()
Заменим
![]() ,
и выполним домножение обеих частей
,
и выполним домножение обеих частей
уравнения на
![]() .
Учитывая, что
.
Учитывая, что
![]() ,
имеем:
,
имеем:
![]()
![]()
Замена:
![]()
![]() .
.
![]()
Обратная замена:
![]()
![]()
![]()
Ответ:
![]() ;
;
![]() .
.
III. Однородные тригонометрические уравнения.
Однородные тригонометрические уравнения разделяются на два вида:
![]() - однородное
уравнение первой степени;
- однородное
уравнение первой степени;
![]() - однородное
уравнение второй степени.
- однородное
уравнение второй степени.
Разделив обе части
уравнения а) на cosx;
б) на
![]() ,
с учетом, что
,
с учетом, что
![]() ,
получим уравнения:
,
получим уравнения:
![]() - простейшее;
- простейшее;
![]() - квадратное.
- квадратное.
Рассмотрим несколько решений однородных уравнений:
Пример 11.
Решите уравнение:
![]()
![]()
![]()
![]()
Ответ:
![]() .
.
Пример 12.
Решите уравнение:
![]()
![]()
Решив это уравнение, получим:
![]()
![]()
Ответ:![]() ;
;
![]() .
.
Если в однородном
уравнении второй степени присутствует
свободный член
![]() ,
то его можно заменить:
,
то его можно заменить:
![]() .
.
Пример 13.
Решите уравнение:
![]()
![]()
![]() ,
,
откуда
![]() ,
,
т.е.
![]()
![]()
Ответ:
![]() ;
;
![]() .
.
Пример 14.
Решите систему уравнений:
![]()
Из первого уравнения
системы находим
![]() .
.
Тогда второе
уравнение системы примет вид:
![]() .
.
Упростим правую часть уравнения:
![]()
![]()
Таким образом,
уравнение примет вид
![]() ,
,
откуда
![]() или
или
![]()
Так как
![]()
![]()
Ответ:
![]()
Существует еще несколько способов решения тригонометрических уравнений, которые при необходимости можно найти в справочниках по математике.
Рассмотренные в данном пункте методы решения тригонометрических уравнений являются базовыми и обязательны к изучению.
№ 53. Решите уравнение:
|
|
|
№ 54*.
Решите уравнение
![]() и найдите сумму его решений на отрезке
и найдите сумму его решений на отрезке
![]()
№ 55*.
Найдите (в градусах) все решения уравнения
![]() ,
удовлетворяющие условию
,
удовлетворяющие условию
![]() .
.
№ 56. Решите уравнение:
![]()
![]()
№ 57. Решите уравнение:
![]()
![]()
![]()
![]()
![]()
№ 58*.
Найдите все решения уравнения
![]() принадлежащие отрезку
принадлежащие отрезку
![]() .
.
№ 59*.
Упростите выражение
![]() и укажите х, при которых его значение
равно
и укажите х, при которых его значение
равно
![]()
№ 60. Решите уравнение:

![]()
![]()
![]()
№ 61*.
Найдите все решения уравнения
![]() ,
лежащие в интервале
,
лежащие в интервале
![]()
№ 62. Решите уравнение
|
|
№ 63. Укажите наименьшее положительное число х, при котором:
![]() ;
;
![]() ;
;
в)
значение выражения
![]() равно
равно
![]() ;
;
г)
значение выражения
![]() равно 0,5.
равно 0,5.
№ 64. Решите уравнение:
|
|
№ 65. Решите уравнение:
|
|
№ 66. Решите уравнение:
|
|
№ 67. Решите систему уравнений:
|
|
№ 68*. Найдите все решения уравнения, принадлежащие заданному отрезку:
|
|
№ 69*. Решите уравнение:
![]()
![]()
Урок одного уравнения: sin x + cos x = 1
Данный подпункт дает представление о наиболее часто встречающихся способах решения тригонометрических уравнений, а также о том, что для тригонометрических уравнений, кром5ке простейших, существует несколько приемов, одновременно позволяющих достичь правильного результата.
I способ. Введение вспомогательного угла.
![]()
![]()
![]()
![]()
![]()
![]()
Изобразим полученное множество решений на единичной окружности и выпишем конечный результат в более компактном виде (это достигается не всегда, но хотя бы черновую проверку делать нужно):
![]()
![]()
![]()
![]()
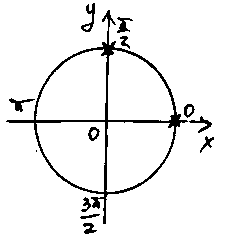
Очевидно, что в
дальнейшем будут получаться только две
серии решений
![]() и
и
![]() .
.
Ответ:
![]()
![]() .
.
II
способ.
Замена sinx
и cosx
через tg![]() .
.
 Следует учесть,
что при переходе к
Следует учесть,
что при переходе к
![]() ,
т.е.
,
т.е.
![]() .
.
Таким образом, заданное уравнение примет вид:
 +
+

![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Ответ:
![]()
![]() .
.
III способ. Сведение к однородному уравнению.
Выразим sinx, сosx и 1 через формулы половинного аргумента:
![]()
Имеем:
![]()
![]()
![]()
![]()
![]()
![]()
Ответ: .
IV способ. Преобразование суммы в произведение.
Используя формулы
приведения, выразим cosx
через
![]() :
:
![]()


![]()
![]()
![]()
Разобьем полученное множество решений на две серии:
![]() и
и
![]()
![]()
![]()
Ответ: .
V способ.
Замена cosx через
![]() .
.
|
|
|
в
Сделав проверку, легко убедиться, что из этой серии решениями уравнения является множество чисел
|
Ответ: .
VI способ. Возведение в квадрат обеих частей уравнения.
![]()
![]()
![]()
или
![]()
![]()
![]()
Проверка:
|
|
Ответ: .
VII способ. Использование формулы:
![]()
![]() и
при
и
при
![]()
![]()
![]()
![]()
![]()
![]()
![]() ;
;
![]() .
.
Ответ: .
IV зачетный раздел
Производные тригонометрических функций и
их применение
п. 21. Таблица производных
Правила дифференцирования
Определение производной*
Пусть х
— произвольная точка лежащая в окрестности
фиксирован-ной точки
![]() .
Разность
.
Разность
![]() называется
приращением
аргумента
в точке
,
т.е.
называется
приращением
аргумента
в точке
,
т.е.
![]() (первоначальное значение аргумента
получи-ло
приращение
(первоначальное значение аргумента
получи-ло
приращение
![]() ).
При изменении аргумента изменяется и
значение функции. Разность
).
При изменении аргумента изменяется и
значение функции. Разность
![]() — называется
приращением
функции
— называется
приращением
функции
![]() в точке
,
соответствующее приращению
в точке
,
соответствующее приращению
![]() .
.
● Производной
функции f
в точке х0
называется
число, к которому стремится разностное
отношение
![]() .
.
Производная функции
f
в точке
обозначается
![]() и
читается: «Эф штрих от
».
и
читается: «Эф штрих от
».

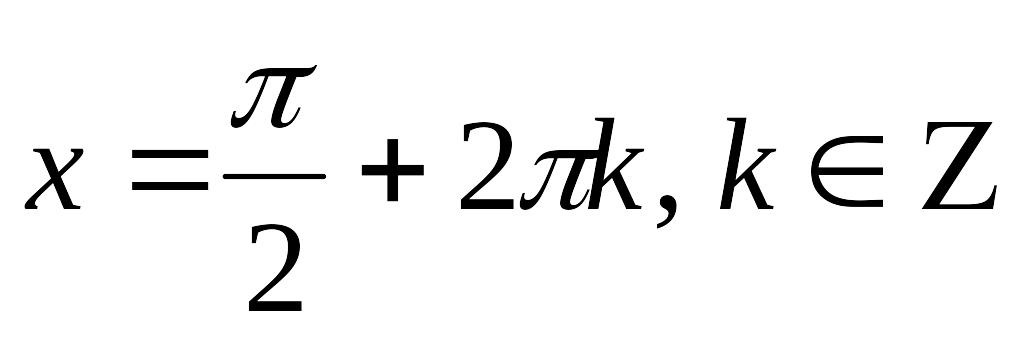
 озведем
в квадрат обе части уравнения и
используем формулы сокращенного
умножения.
озведем
в квадрат обе части уравнения и
используем формулы сокращенного
умножения.