П. 17. Формулы приведения и их применение

Из всех существующих способов задания формул приведения оптимальным является следующая таблица:

			-		-	-		-
	-		-	-		-
	-			-	-			-
	-			-	-			-

Напомним, что

К наиболее распространенным случаям применения формул относят перевод тригонометрических функций углов: ; ; к тригонометрическим функциям угла .

Пример 1. Упростите выражения:

С помощью формул приведения нахождение значений тригонометрических функций любого угла можно свести к нахождению значений тригонометрических функций угла от 0 до .

Пример 2. Приведите угол к промежутку и найдите его значение:

№ 40. Приведите к тригонометрической функции угла .

№ 41. Приведите к тригонометрической функции угла

№ 42. Преобразуйте выражение:

№ 43*. Найдите числовое значение выражения:

П. 18. Формулы двойного и половинного угла

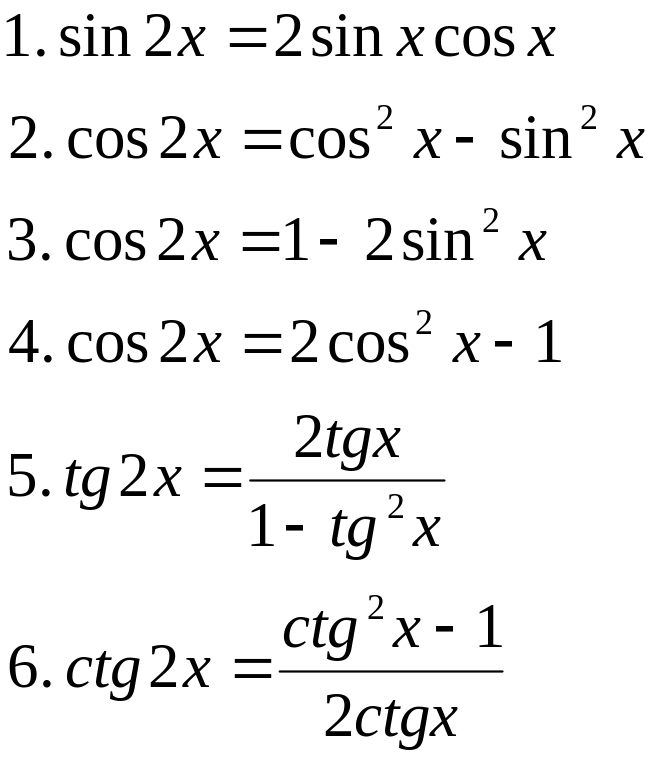
Приведенные формулы позволяют выразить тригонометрические функции углов через тригонометрические функции угла х.

Рассмотрим основные примеры по их применению:

Пример 1. Вычислите:

, если

Найдем сначала значение (см. п.7):

.

Далее подставим в формулы двойного и половинного угла известные

значения: ;

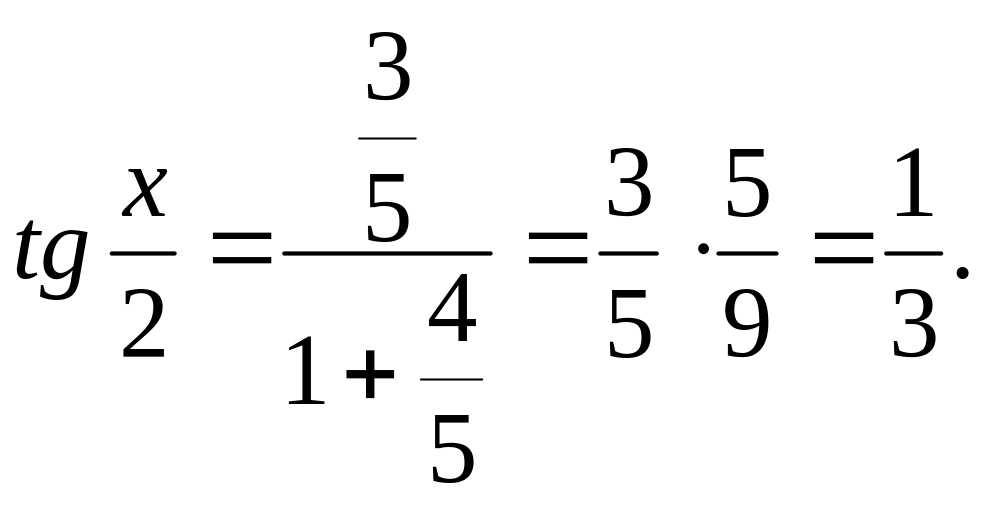
Формулы двойного и половинного угла используются и в преобразованиях выражений, приведя их к функциям одного угла.

Пример 2. Упростите выражения:

№ 44. Найдите значение выражения:

№ 45. Упростите выражение:

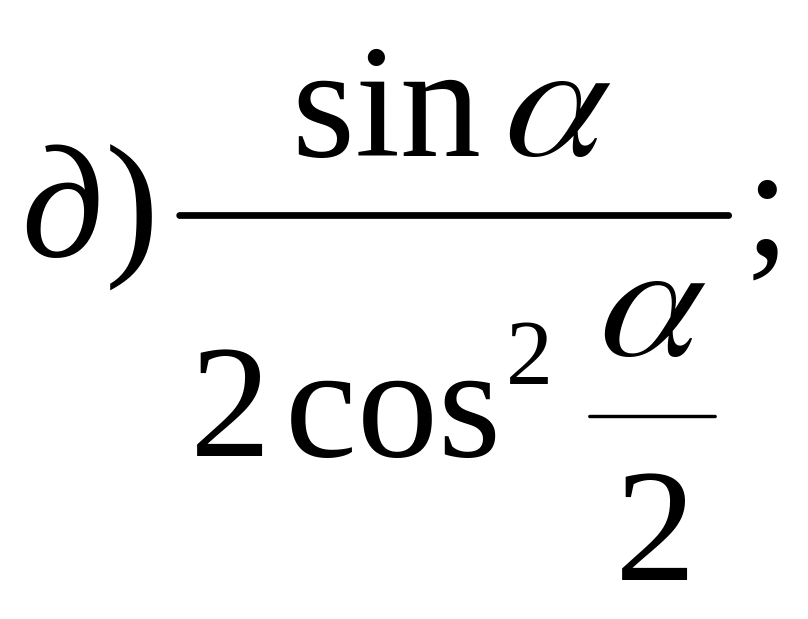
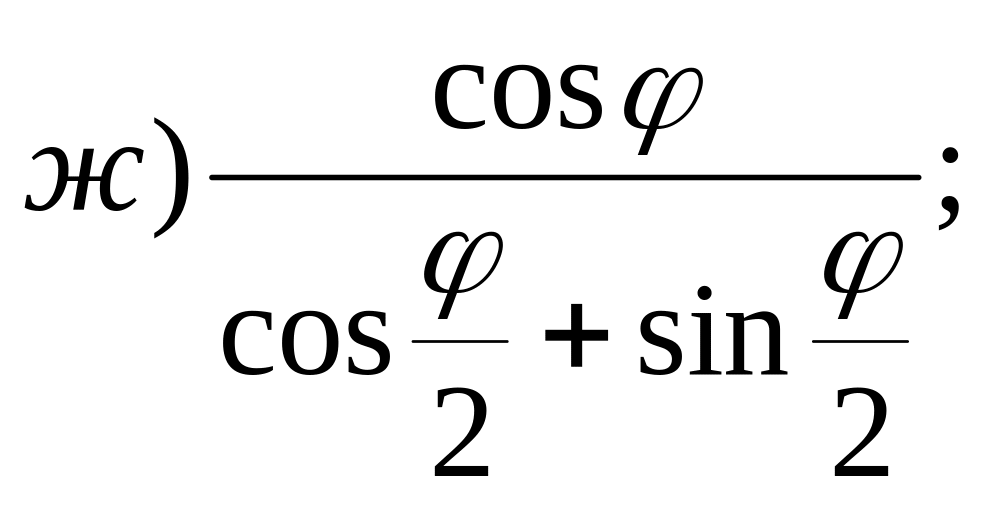
№ 46. Упростите:

№ 47*. Вычислите:

№ 48*. Докажите тождество:

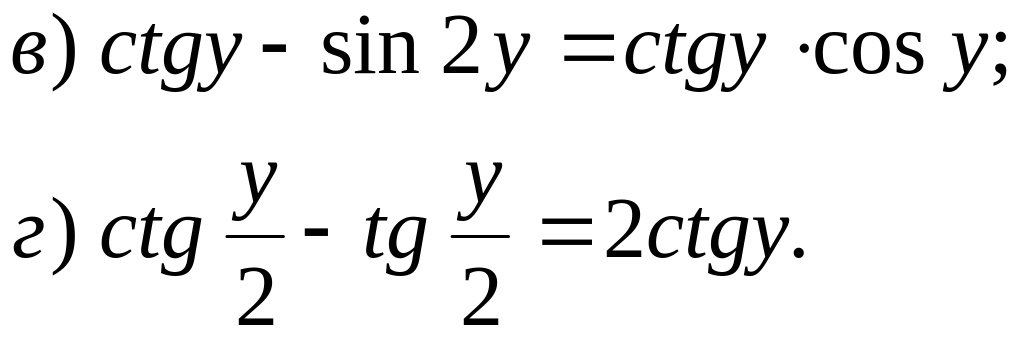
П. 19. Формулы суммы и разности тригонометрических функций

Сумму и разность тригонометрических функций можно представить в виде произведения с помощью формул сложения.

Приведем несколько примеров применения данных формул:

Пример 1. Упростите выражение:

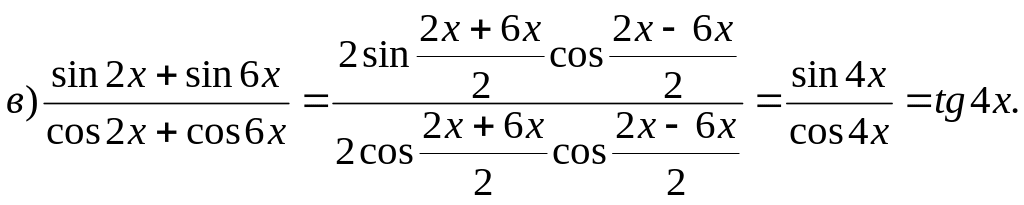
При выполнении задания следующего примера следует обратить внимание на то, что недостающую для применения формул тригонометрическую функцию следует взять из таблицы значений, см. п. 4.

Пример 2. Представьте выражение в виде произведения:

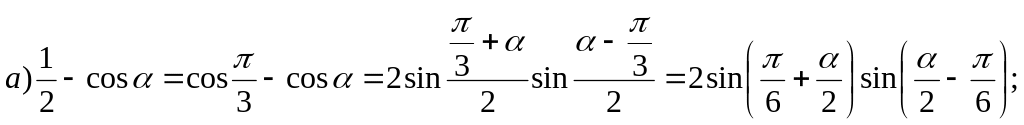
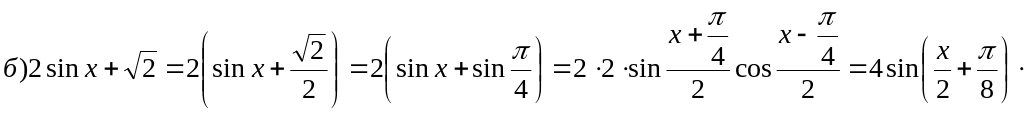
№ 49. Представьте в виде произведения:

№ 50. Упростите выражение:

;

;

; .

№ 51. Вычислите:

; ; .

; ;

№ 52*. Сравните значения выражений:

.