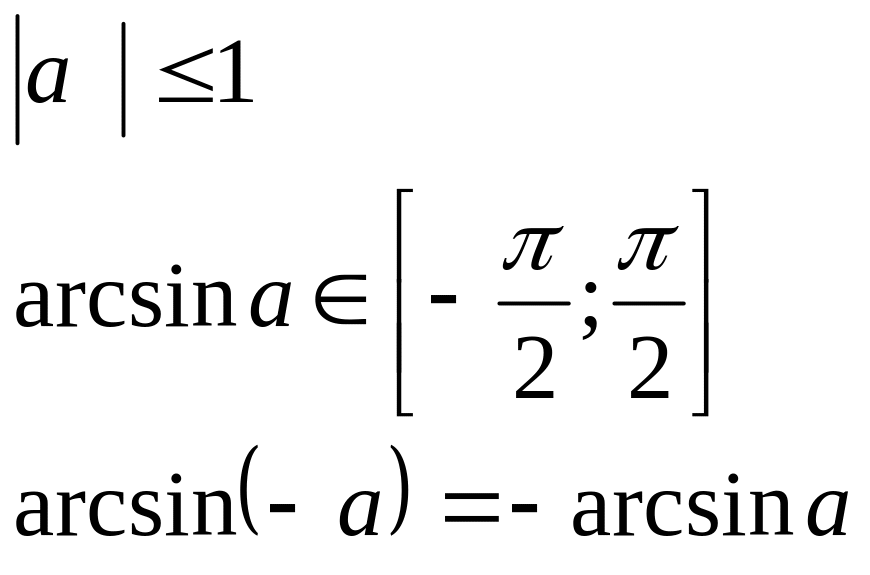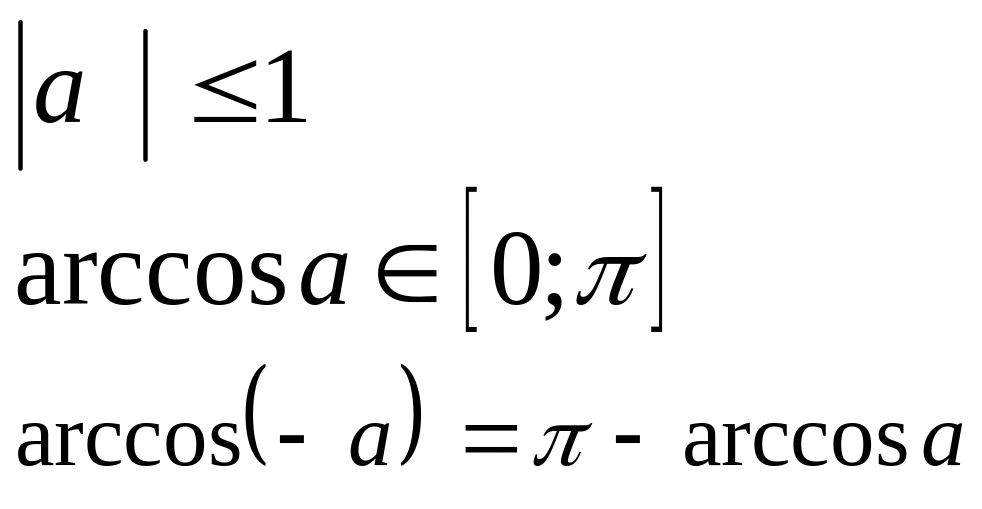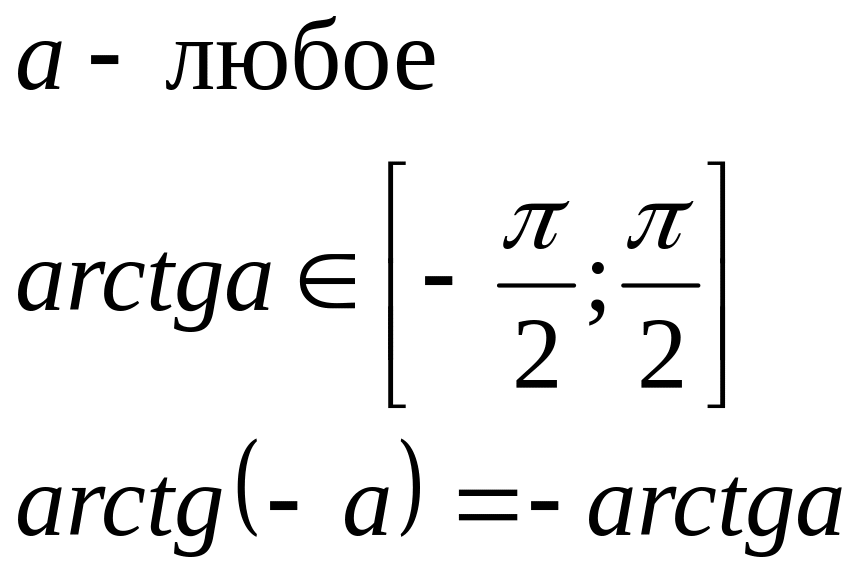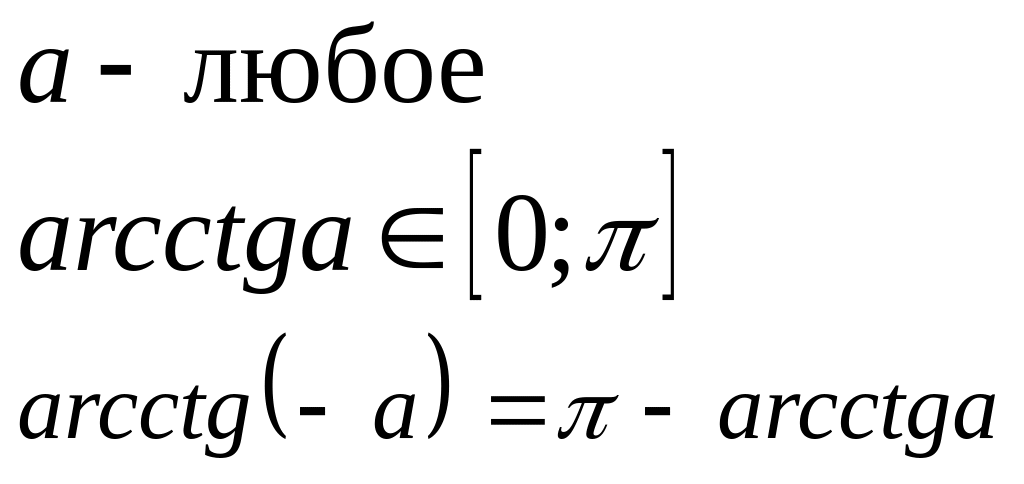П. 13. Обратные тригонометрические функции

Используются при решении тригонометрических уравнений и неравенств, создают более широкую базу для применения тригономет-рических функций. Сформулируем утверждение, которым удобно пользоваться при решении уравнений:

Теорема (о корне). Пусть функция возрастает (убывает) на промежутке J, число а – любое из значений, принимаемых на этом промежутке. Тогда уравнение =а имеет единственный корень в промежутке J.

Воспользовавшись теоремой, получим следующее утверждение: так как функция (рис. 8) возрастает на отрезке и принимает на нем все значения от -1 до 1 , то для любого числа а, такого, что существует единственный корень в уравнении sinx=а.

Это число называют арксинусом числа а и обозначают arcsin a:

при этом

Пример:

Аналогично выводятся понятия:

арккосинуса при этом

арктангенса при этом

арккотангенса при этом

Примеры:

.

№ 23. Вычислите:

№ 24. Найдите значение выражения:

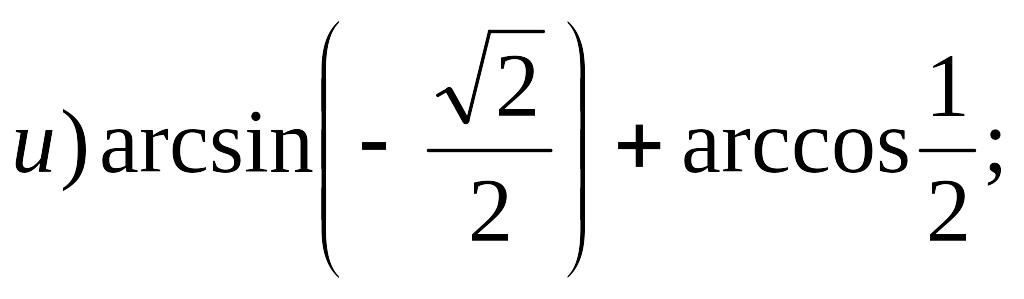
№ 25*. Вычислите:

№ 26. Сравните числа:

№ 27*. Найдите значение выражения:

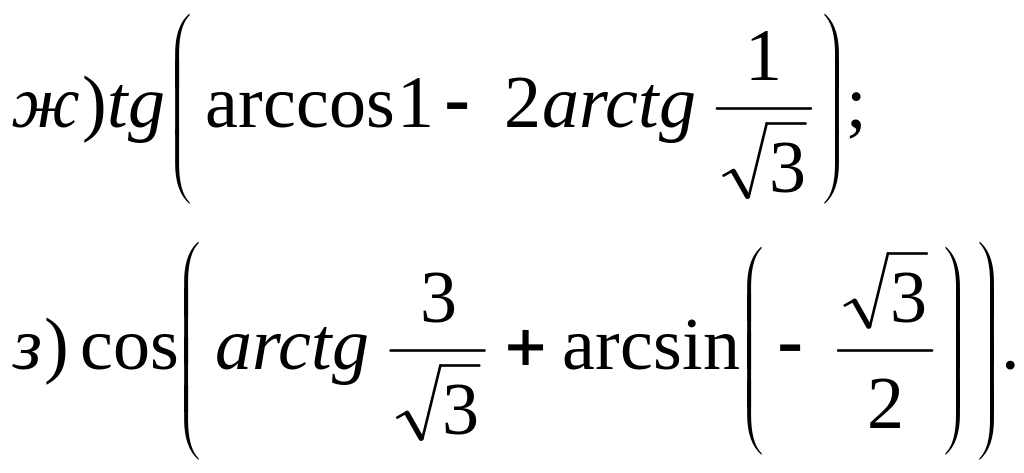
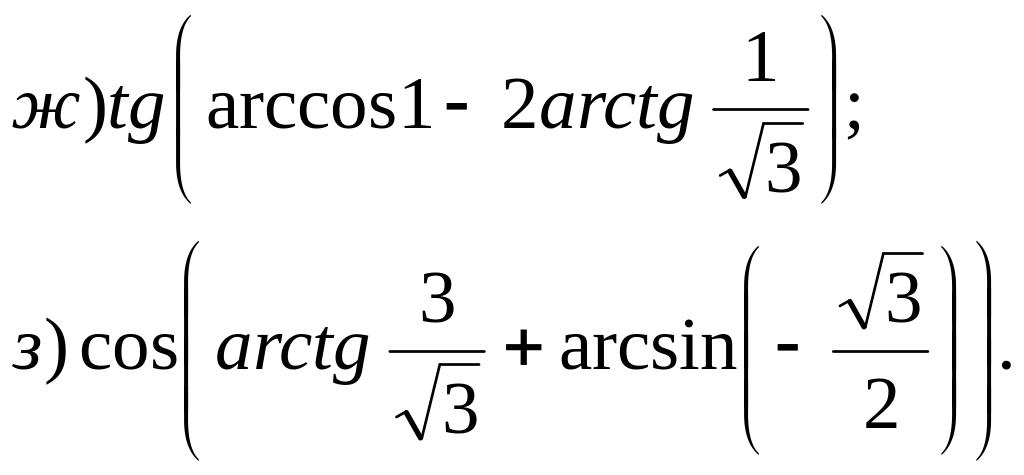
П. 14. Простейшие тригонометрические уравнения

В п.13 было выведено утверждение о том, что уравнение sinx=0, где , имеет на промежутке единственный корень.

Но так как область определения функции y=sinx – множество действительных чисел, то очевидно, что уравнение sinx=а, где , на интервале имеет бесконечное множество решений. Графически корни уравнения sinx=a, где , есть абсциссы точек пересечения синусоиды y=sinx и прямой y=a.

Рассмотрим для примера графическое решение уравнения .

Рисунок 16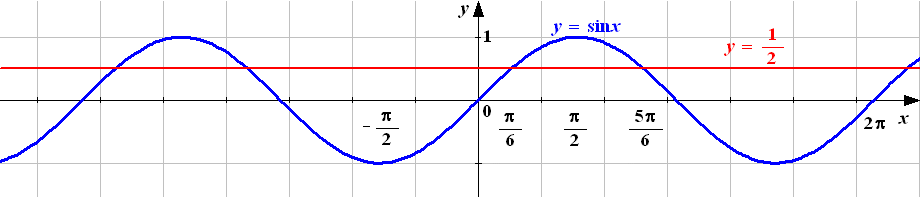

На промежутке уравнение имеет два корня: . Очевидно, что в силу периодичности функции y=sinx для нахождения множества всех решений уравнения нужно к каждому из найденных корней прибавить числа вида , где .

Полученные множества решений уравнения можно искусственно объединить в одну формулу: .

На практике при решении простейших тригонометрических уравнений удобнее пользоваться стандартными формулами:

Урав-нение	Решение	Частные случаи	Примечания
sinx=a
cosx=a
tgx=a
ctgx=a

Пример: Решите уравнение:

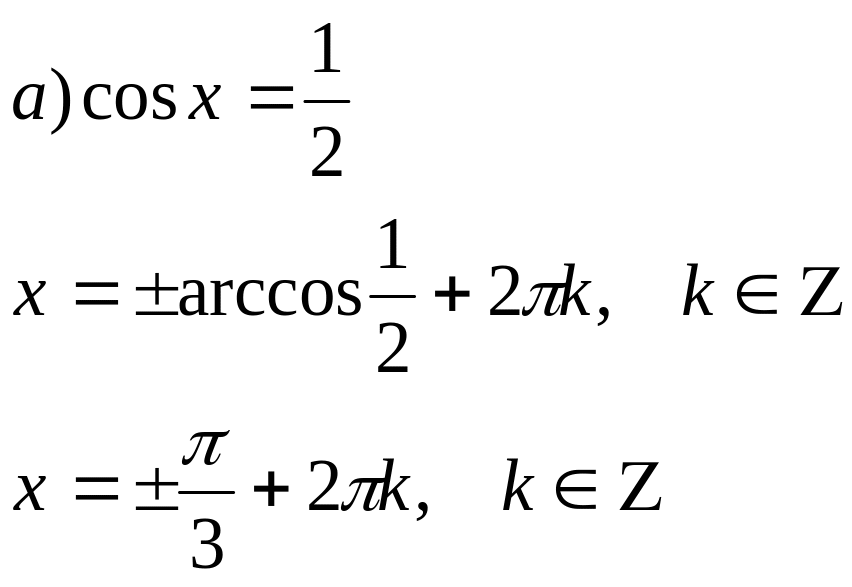
Ответ: .

б)

Ответ:

в)

Ответ:

г)

Ответ:

д)

Преобразуем выражение

2

Ответ:

е)

Ответ:

ж) , т.к. аргумент у косинуса – сложная функция, то уравнение решают сначала относительно , а затем выражают .

Ответ:

з)

Ответ:

№ 28. Решите уравнение:

№ 29. Решите уравнение:

№ 30. Решите уравнение:

а)

№ 31. Решите уравнение:

№ 32*. Найдите все решения уравнения , которые являются также решениями уравнения .

№ 33*. Найдите (в градусах) решения уравнения , принадлежащие интервалу .