
- •Тригонометрические функции. Преобразования тригонометрических выражений Пособие для учащихся 11 класса
- •От автора
- •Введение
- •П. 2. Формулы перевода углов из градусной меры в радианную, и наоборот
- •П. 3. Определение тригонометрических функций
- •П. 4. Таблица значений тригонометрических функций
- •П. 5. Свойства тригонометрических функций
- •П. 6. Азбука тригонометрии
- •П. 7. Нахождение значений тригонометрических функций
- •Линия котангинса
- •П. 12. Преобразования графиков
- •П. 13. Обратные тригонометрические функции
- •П. 14. Простейшие тригонометрические уравнения
- •П. 15. Простейшие тригонометрические неравенства
- •П. 17. Формулы приведения и их применение
- •П. 18. Формулы двойного и половинного угла
- •П. 19. Формулы суммы и разности тригонометрических функций
- •III зачетный раздел Тригонометрические уравнения п. 20. Методы решения тригонометрических уравнений
- •Упрощение уравнения, используя тригонометрические формулы.
- •II. Метод введения новой переменной
- •III. Однородные тригонометрические уравнения.
- •Алгоритм отыскания производной функции :
- •Правила дифференцирования
- •П. 22. Применение производной
- •Физический смысл производной.
- •Геометрический смысл производной.
- •Алгоритм составления уравнения касательной к графику функции:
- •III. Исследование функции на монотонность и экстремум.
- •IV. Применение производной к построению графика функции.
- •V. Отыскание наибольшего и наименьшего значений непрерывной функции на отрезке .
- •Справочный раздел
- •Ответы, указания, решения
- •Литература
- •Содержание
- •Тригонометрические функции. Преобразование тригонометрических выражений
- •Г. Новокузнецк, ул.Транспортная, 17
 ,
кєΖ.
,
кєΖ.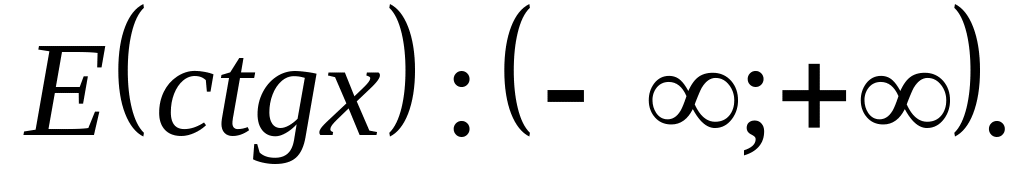
Функция периодическая с основным периодом .
Функция нечетная.
Е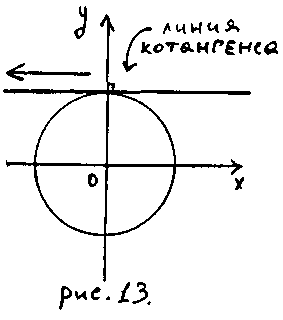
Рисунок 14
Линия котангинса
а) Функция убывает на
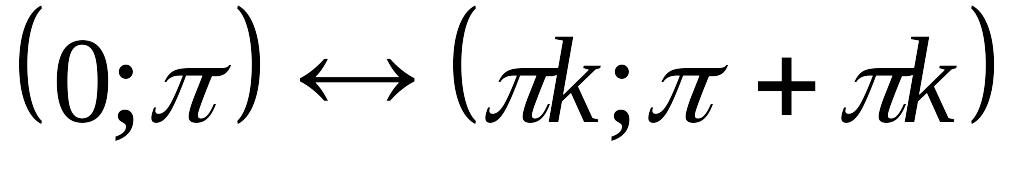 (с
увеличением
,
x
– уменьшается), кєΖ;
(с
увеличением
,
x
– уменьшается), кєΖ;б) Функция положительна на ,
в) Функция отрицательна на ,
г) Нули функции
сли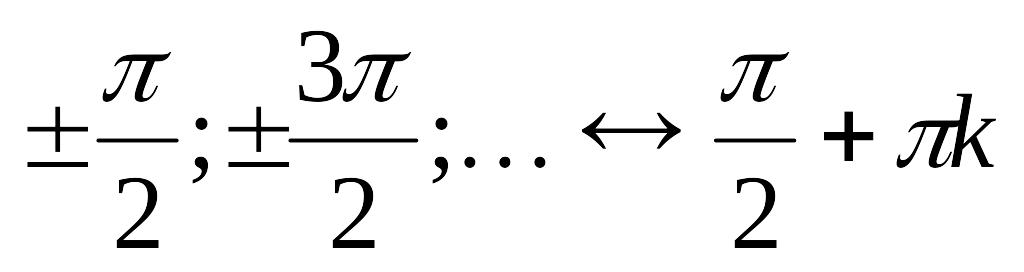 ,
кєΖ.
,
кєΖ. и (см. рис.13 и рис.14):
и (см. рис.13 и рис.14):
П. 12. Преобразования графиков
Приведенная ниже таблица позволяет существенно расширить возможности построения графиков функций по заданному графику элементарной функции.
Функция |
Формула, задающая преобразование |
Преобразование,
которое следует провести с графиком |
|
|
|
Сжатие вдоль оси
OX
отно-сительно оси ОY
в k
раз, если k>1;
растяжение в
|
I |
|
|
Сдвиг вправо по
оси OX
на
|
II |
|
|
Растяжение вдоль оси OY относи-тельно оси OX в k раз, если k>1; сжатие вдоль оси OY раз, если 0<k<1 |
III |
|
|
Cдвиг
вверх по оси OY
графика функции
на А единиц, если А>0; сдвиг вниз на
|
IV |
|
|
Симметричное отображение графика относительно оси OY |
V |
|
|
Симметричное отображение гра-фика относительно оси OX |
VI |
Если функция
|
VII |
||
Замечания:
При использовании таблицы желательно пользоваться указанными пунктами по порядку, т.е. с I по VΙΙ.
При построении графика периодической функции нужно вначале вычислить (используя VII) её наименьший положительный период и на нем строить график заданной функции.
Приведем примеры по применению таблицы к построению графиков тригонометрических функций.
Пример 1
Построить графики функций:
![]()
Используем за
основу график функции
![]() ,
VII,
I
строки таблицы:
,
VII,
I
строки таблицы:
 — периодическая
функция, с периодом
— периодическая
функция, с периодом
 ,
при этом преобразовании происходит
сжатие графика функции
в 3 раза.
,
при этом преобразовании происходит
сжатие графика функции
в 3 раза. — периодическая
функция, с периодом
— периодическая
функция, с периодом
 ,
— растяжение графика функции
в 2 раза.
,
— растяжение графика функции
в 2 раза.

Пример 2
Построить графики функций:
![]()
Используем за
основу график функции
![]() ,
VII,
II
строки таблицы:
,
VII,
II
строки таблицы:
— периодическая функция, с периодом
 ,
при этом преобразовании происходит
сдвиг графика функции
вправо на
,
при этом преобразовании происходит
сдвиг графика функции
вправо на
 ,
(т.е.
=6/4=1,5
клетки).
,
(т.е.
=6/4=1,5
клетки). — периодическая
функция, с периодом
,
— сдвиг влево на
— периодическая
функция, с периодом
,
— сдвиг влево на
 (т.е. на 6 клеток).
(т.е. на 6 клеток).
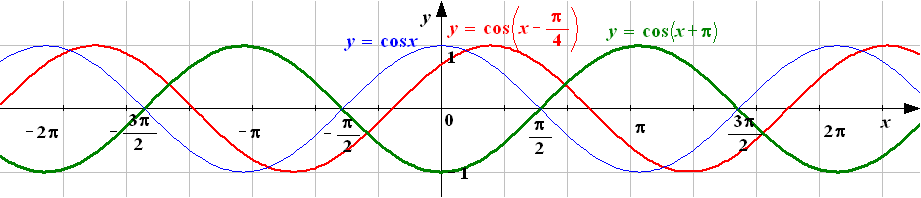
Пример 3
Построить графики функций:
![]()
Используем за основу график функции , VII, III строки таблицы:
— периодическая функция, с периодом , при этом преобразовании происходит растяжение графика функции в 3 раза.
— периодическая функция, с периодом , — сжатие графика функции в 2 раза.

Пример 4
Построить графики функций:
![]()
Используем за основу график функции , VII, IV строки таблицы:
 — периодическая
функция, с периодом
,
при этом преобразовании происходит
сдвиг графика функции
вверх на 1, (т.е. 1 = 2 клетки).
— периодическая
функция, с периодом
,
при этом преобразовании происходит
сдвиг графика функции
вверх на 1, (т.е. 1 = 2 клетки). — периодическая
функция, с периодом
,
— сдвиг вниз на 2 (т.е. на 4 клетки).
— периодическая
функция, с периодом
,
— сдвиг вниз на 2 (т.е. на 4 клетки).

Рассмотрим более сложный пример:
Постройте график
функции
![]() и опишите её свойства.
и опишите её свойства.
Решение:
Данная функция образована с помощью
функции
c
периодом Т=2
.
Вычислим период заданной функции:
![]() .
.
Представим данную функцию в виде цепочки преобразований, сводящих её от простой к заданной:

Используя контрольные точки графика функции y=sinx на отрезке , проследим, куда они перейдут при дальнейших преобразованиях (см. таблицу).
Построим на XOY график по точкам:
![]() ,
рис.15.
,
рис.15.
Начнем рассматривать
преобразования графика с изменения
аргумента:
![]() - сжатие вдоль оси OX
в 2 раза,
- сжатие вдоль оси OX
в 2 раза,
![]() рис. 15, см.
рис. 15, см.
![]() .
.
Заметим, что функция
![]() ,
,
т.е. (после сжатия)
недостающий сдвиг влево – равен
![]() ,
,
![]() .
Рис. 15, см.
.
Рис. 15, см.
![]() .
.
Далее идут преобразования значений функции:
![]() - расстояние вдоль
оси OY
в 5 раз,
- расстояние вдоль
оси OY
в 5 раз,
![]() .
Рис. 15, см.
.
Рис. 15, см.
![]() .
.
![]() - сдвиг вдоль оси
OY
вниз на 1 единицу,
- сдвиг вдоль оси
OY
вниз на 1 единицу,
![]() .
Рис. 15, см.
.
Рис. 15, см.
![]() .
.
Так как
![]() - периодична, то полученный график
следует отобразить на всю область
определения.
- периодична, то полученный график
следует отобразить на всю область
определения.
Рисунок 15









О пишем
свойства функции
,
по графику, учитывая период
пишем
свойства функции
,
по графику, учитывая период
![]() :
:


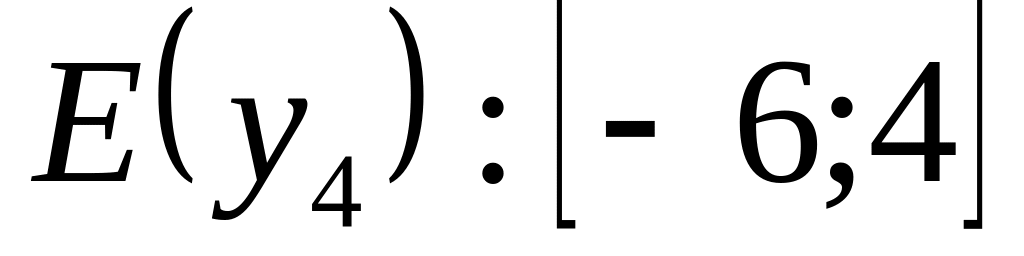 ;
;функция возрастает на
 ;
;функция убывает на
 ;
;функция положительна на
 ;
;функция отрицательна на
 ;
;нули функции при
 ;
;наибольшие значения функции равны 4 и достигаются в точках
 ;
;наименьшие значения функции равны -6 и достигаются в точках
 ,
,
 ;
;точки, в которых касательные параллельны оси OX, имеют абсциссы

Заметим, что свойства, выписанные с использованием графика, носят приблизительные значения в связи с погрешностью построения.
№ 22. Найдите наименьший положительный период функции и опишите их свойства, выполнив построение графика:



